Last bit of homework I need help with! It's python and computational modeling. Thanks for all your help! I've listed q7 and q9 to reference.

THANK YOU

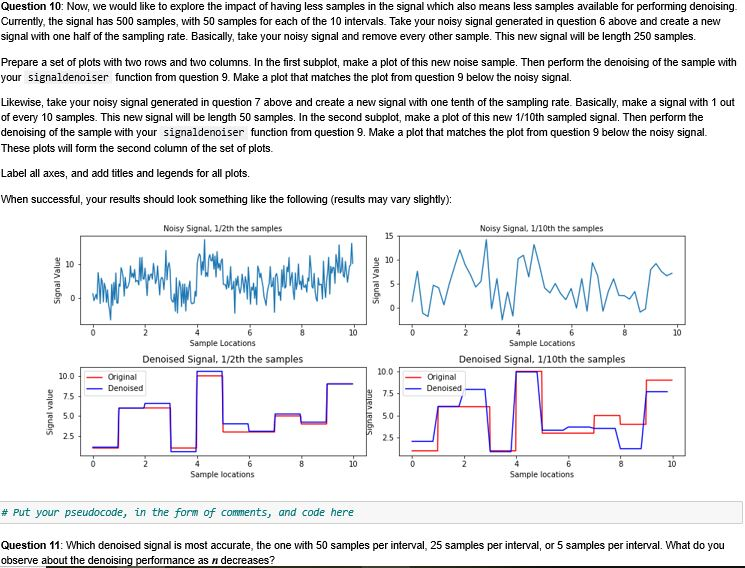
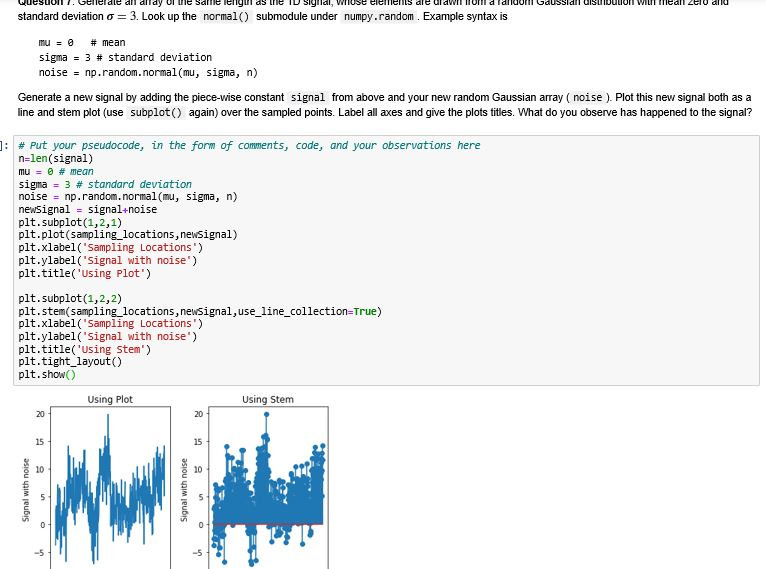
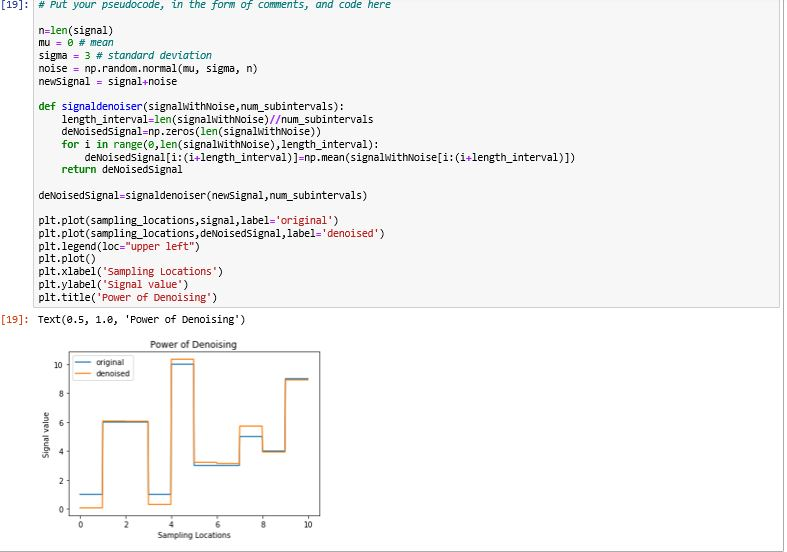
Question 10: Now, we would like to explore the impact of having less samples in the signal which also means less samples available for performing denoising. Currently, the signal has 500 samples, with 50 samples for each of the 10 intervals. Take your noisy signal generated in question 6 above and create a new signal with one half of the sampling rate. Basically, take your noisy signal and remove every other sample. This new signal will be length 250 samples. Prepare a set of plots with two rows and two columns. In the first subplot, make a plot of this new noise sample. Then perform the denoising of the sample with your signaldenoiser function from question 9. Make a plot that matches the plot from question 9 below the noisy signal. Likewise, take your noisy signal generated in question 7 above and create a new signal with one tenth o of every 10 samples. This new signal will be length 50 samples. In the second subplot, make a plot of this new 1/10th sampled signal. Then perform the denoising of the sample with your signaldenoiser function from question 9. Make a plot that matches the plot from question 9 below the noisy signal. These plots will form the second column of the set of plots. Label all axes, and add titles and legends for all plots. When successful, your results should look something like the following (results may vary slightly): Noisy Signal, 1/2th the samples Noisy Signal, 1/10th the samples Signal Value Signal Value 10 Sample Locations Denoised Signal, 1/2th the samples Original Denoised Sample Locations Denoised Signal. 1/10th the samples Original Denoised - Signal value Signal value Sample locations Sample locations # Put your pseudocode, in the form of comments, and code here Question 11: Which denoised signal is most accurate, the one with 50 samples per interval, 25 samples per interval, or 5 samples per interval. What do you observe about the denoising performance as n decreases? WuesuullI. Genelde dll dlldy Ul une salle lenyul as the IU Signal, WIuse elements de udWII HUMI didur GOUSSIdll UsubuLUN WILT medll ZIU dll standard deviation o = 3. Look up the normal() submodule under numpy.random. Example syntax is mu = 0 # mean sigma = 3 # standard deviation noise = np.random.normal (mu, sigma, n) Generate a new signal by adding the piece-wise constant signal from above and your new random Gaussian array (noise ). Plot this new signal both as a line and stem plot (use subplot() again) over the sampled points. Label all axes and give the plots titles. What do you observe has happened to the signal? # Put your pseudocode, in the form of comments, code, and your observations here n=len(signal) mu = # mean sigma = 3 # standard deviation noise = np.random. normal(mu, sigma, n) newSignal = signal-noise plt. subplot(1,2,1) plt.plot(sampling_locations, newSignal) plt.xlabel('Sampling Locations) plt.ylabel('Signal with noise) plt. title('Using Plot') plt.subplot(1,2,2) plt.stem( sampling_locations, newsignal, use_line_collection=True) plt.xlabel('Sampling Locations) plt.ylabel('Signal with noise) plt.title('Using Stem') plt. tight_layout() plt.show Using Plot Using Stem Signal with noise Signal with noise [19]: # Put your pseudocode, in the form of comments, and code here n=len(signal) mu = @ # mean sigma = 3 # standard deviation noise = np.random.normal (mu, sigma, n) newsignal = signal+noise def signaldenoiser(signalwithNoise, num subintervals): length_interval=len(signalwithNoise)/um_subintervals denoisedSignal=np.zeros(len(signalwithNoise)) for i in range(0, len(signalwithNoise), length_interval): deNoisedSignal[i:(i+length_interval)]=np.mean(signalwithNoise[i:(i+length_interval)]) return deNoisedSignal deNoisedSignal-signaldenoiser(newSignal, num subintervals) plt.plot(sampling_locations, signal, label='original') plt.plot(sampling locations, deNoisedSignal, label='denoised') plt.legend(loc="upper left") plt.plot() plt.xlabel('Sampling Locations) pit.ylabel('Signal value') plt.title('Power of Denoising') [19]: Text(0.5, 1.0, 'Power of Denoising') Power of Denoising - original -denoised Signal value Sampling Locations