Question
Let A = {0^n | n is prime}.(A is not DFA-recognizable.) Show that A* is DFA-recognizable. 3. Show that there is a language A {0,
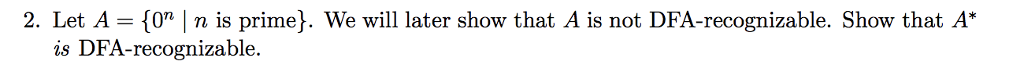 Let A = {0^n | n is prime}.(A is not DFA-recognizable.) Show that A* is DFA-recognizable.
Let A = {0^n | n is prime}.(A is not DFA-recognizable.) Show that A* is DFA-recognizable. 3. Show that there is a language A {0, 1} with the following properties: (a) For all x A, |x| 5. (b) No DFA with fewer than 9 states recognizes A. Hint: You dont have to define A explicitly; just show that it has to exist. Count the number of languages satisfying (4a) and the number of DFAs satisfying (4b), and then use the pigeonhole principle. To count the number of DFAs satisfying (4b), consider that a DFA behaves identically even if you rename all the states, so you can assume without loss of generality that any DFA with k states has the state set {q1, q2, . . . , qk}. Now think about how to count how many ways there are to choose the other parts of the DFA. To count the number of languages satisfying (4a), think about writing down all the strings of length at most 5, and then to define such a language, you have to make a binary decision for each string about whether to include it in the language or not. How many ways are there to make these choices?
3. Show that there is a language A {0, 1} with the following properties: (a) For all x A, |x| 5. (b) No DFA with fewer than 9 states recognizes A. Hint: You dont have to define A explicitly; just show that it has to exist. Count the number of languages satisfying (4a) and the number of DFAs satisfying (4b), and then use the pigeonhole principle. To count the number of DFAs satisfying (4b), consider that a DFA behaves identically even if you rename all the states, so you can assume without loss of generality that any DFA with k states has the state set {q1, q2, . . . , qk}. Now think about how to count how many ways there are to choose the other parts of the DFA. To count the number of languages satisfying (4a), think about writing down all the strings of length at most 5, and then to define such a language, you have to make a binary decision for each string about whether to include it in the language or not. How many ways are there to make these choices?
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


