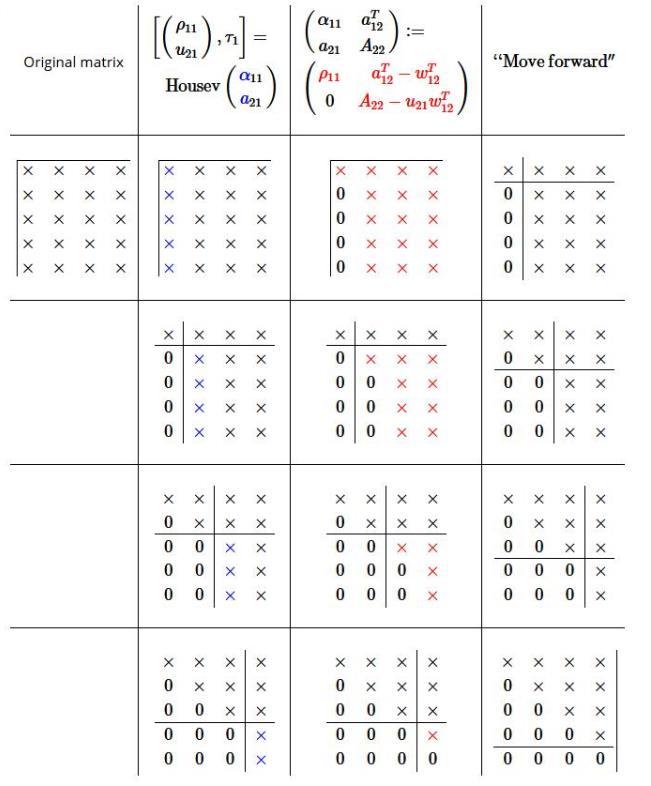
Let A e Rmxn with n >m. In this case, the system is underdetermined: Ar = b has fewer equations than unknowns (elements of 2). Let's assume that the rows of A are linearly indepen- dent (in other words, AT has linearly independent columns). Then instead of computing the QR factorization of A, one may wish to compute the LQ factorization of A: A = LQ where Le Rmxn is lower triangular (has zeroes above its diagonal) and Q is unitary. Illustrate zeroes are introduced in each step similar to the picture 11 1 121 Original matrix . ) - ur. A22 21. Move forward 110 P11 Housev 021 0 xxxxx X X X x x x x x x x x x x x x x x x x x x x x x x xxx x x x x x x x x x x 0 x x x x x 0 0 0 0 X X X X X X x x x x 0 X 0 X X X X xxx XX xx X X X x x x x x 0 0 0 0 0 0 0 0 0 0 0 0 0 xx X X 0 0 0 0 0 xxx X X X X X X xx Olxx ox x xxx 0 0 0 0 0 XOOO X X X X | x x x xxx 0 0 0 0 0 0 0 0 0 X X 0 0 0 xx X X X 0 0 0 xxx X X X X 0 0 0 0 0 0 0 0 X X 0 0 0 X 0 0 0 0 0 0 0 0 0 Let A e Rmxn with n >m. In this case, the system is underdetermined: Ar = b has fewer equations than unknowns (elements of 2). Let's assume that the rows of A are linearly indepen- dent (in other words, AT has linearly independent columns). Then instead of computing the QR factorization of A, one may wish to compute the LQ factorization of A: A = LQ where Le Rmxn is lower triangular (has zeroes above its diagonal) and Q is unitary. Illustrate zeroes are introduced in each step similar to the picture 11 1 121 Original matrix . ) - ur. A22 21. Move forward 110 P11 Housev 021 0 xxxxx X X X x x x x x x x x x x x x x x x x x x x x x x xxx x x x x x x x x x x 0 x x x x x 0 0 0 0 X X X X X X x x x x 0 X 0 X X X X xxx XX xx X X X x x x x x 0 0 0 0 0 0 0 0 0 0 0 0 0 xx X X 0 0 0 0 0 xxx X X X X X X xx Olxx ox x xxx 0 0 0 0 0 XOOO X X X X | x x x xxx 0 0 0 0 0 0 0 0 0 X X 0 0 0 xx X X X 0 0 0 xxx X X X X 0 0 0 0 0 0 0 0 X X 0 0 0 X 0 0 0 0 0 0 0 0 0