Answered step by step
Verified Expert Solution
Question
1 Approved Answer
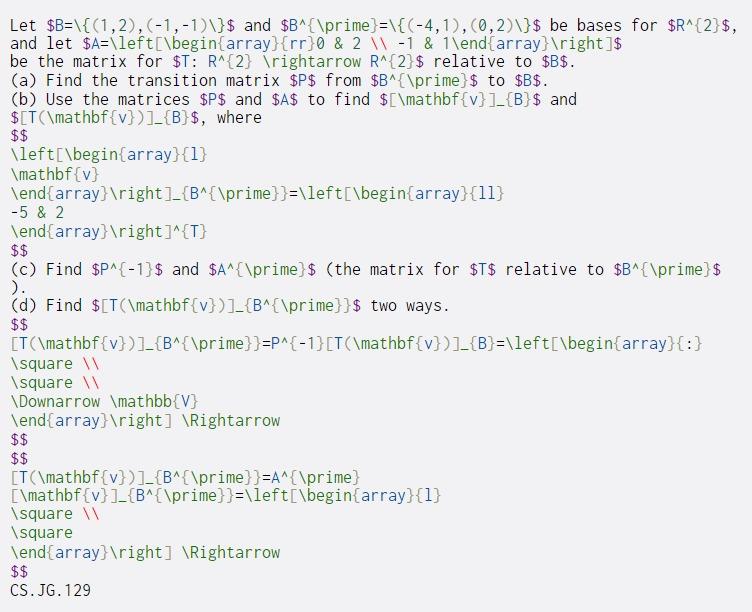
Let $B={(1,2), (-1,-1)}$ and $B^{prime) ={(-4,1),(0,2)}$ be bases for $R^{2}$, and let $A=left[begin{array}{rr}0 & 2 1 -1 & 1end{array} ight]$ be the matrix for $T:
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


