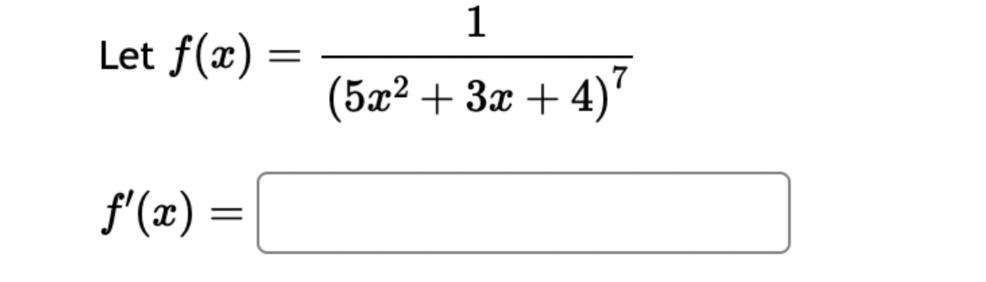
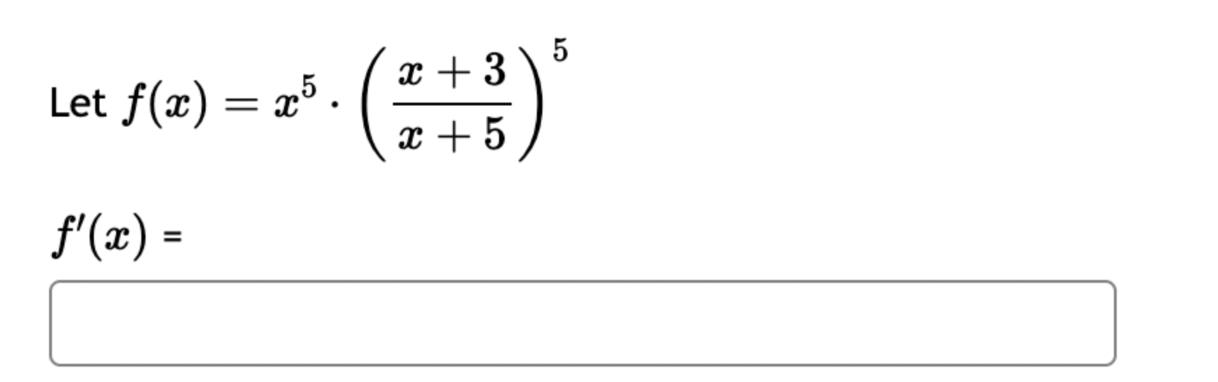
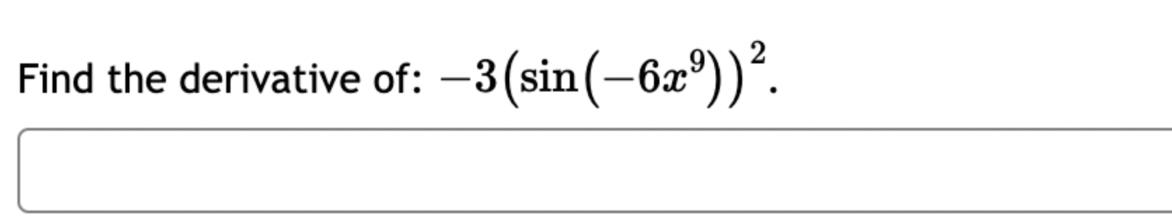
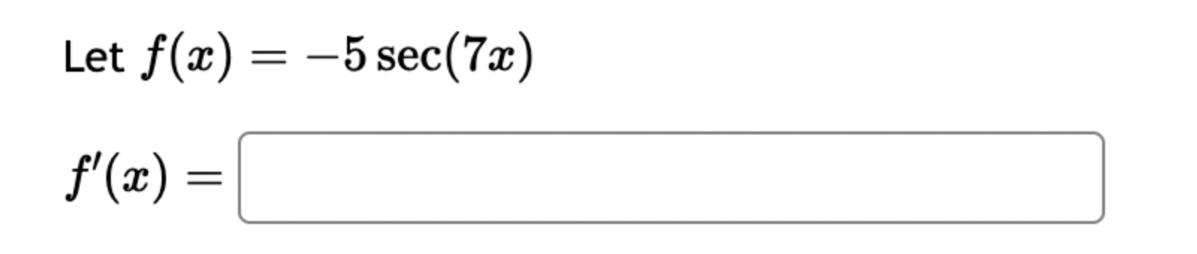
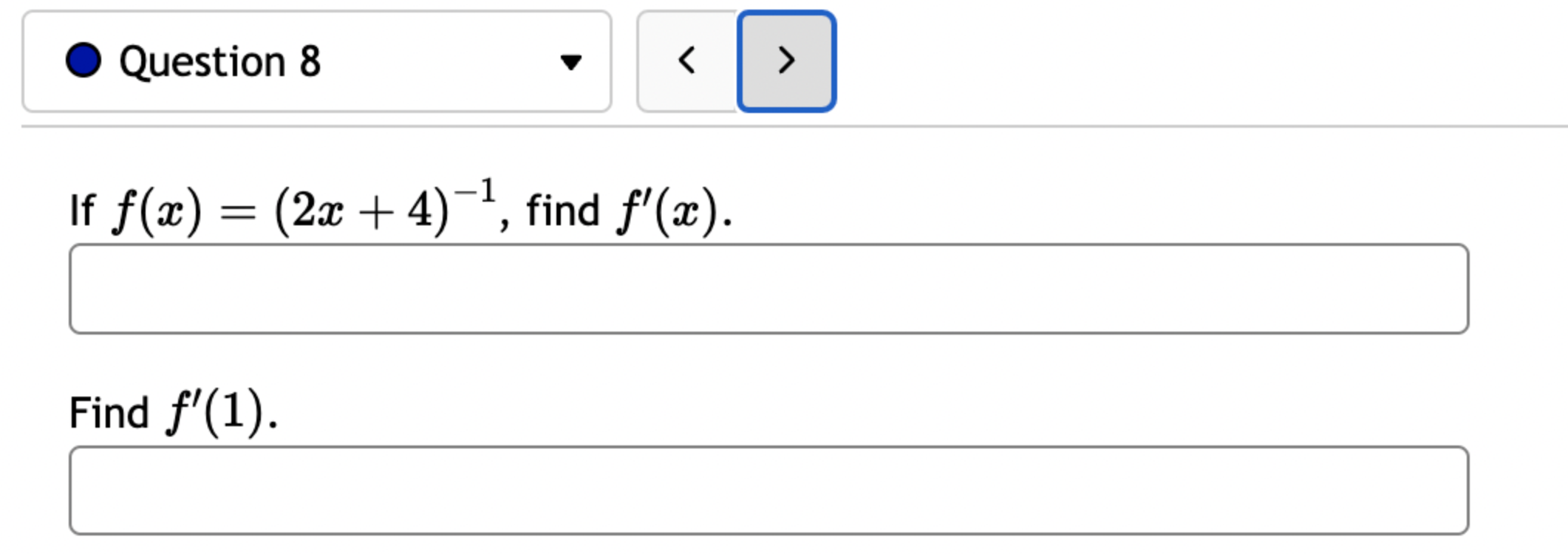
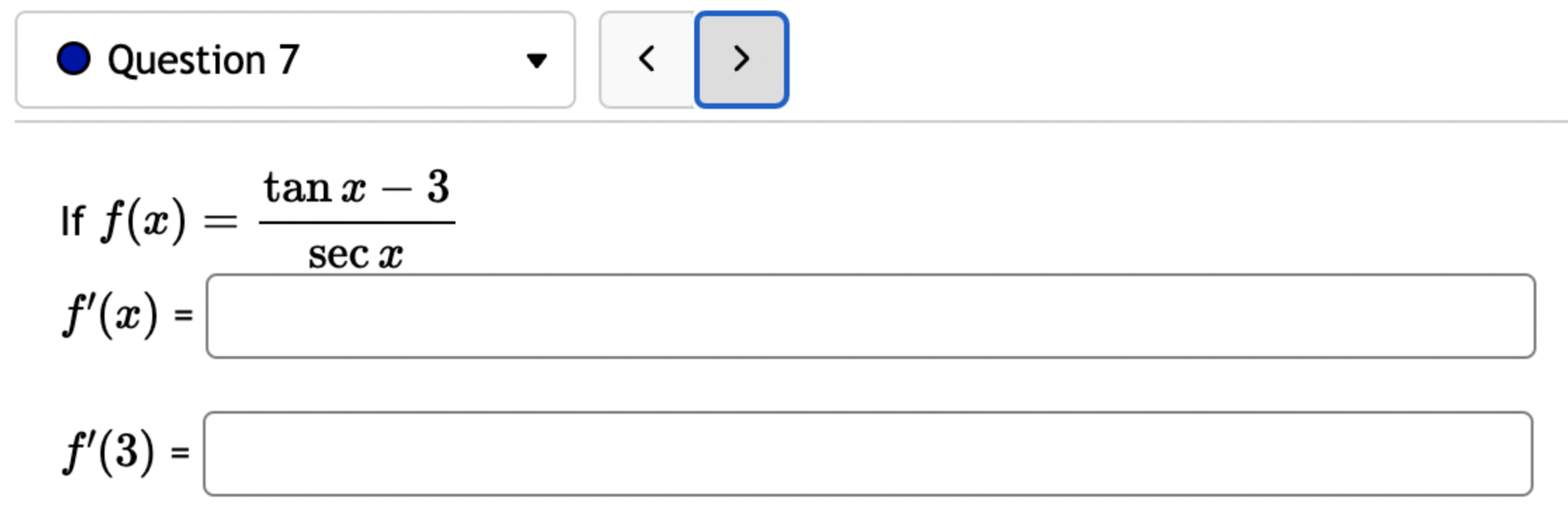
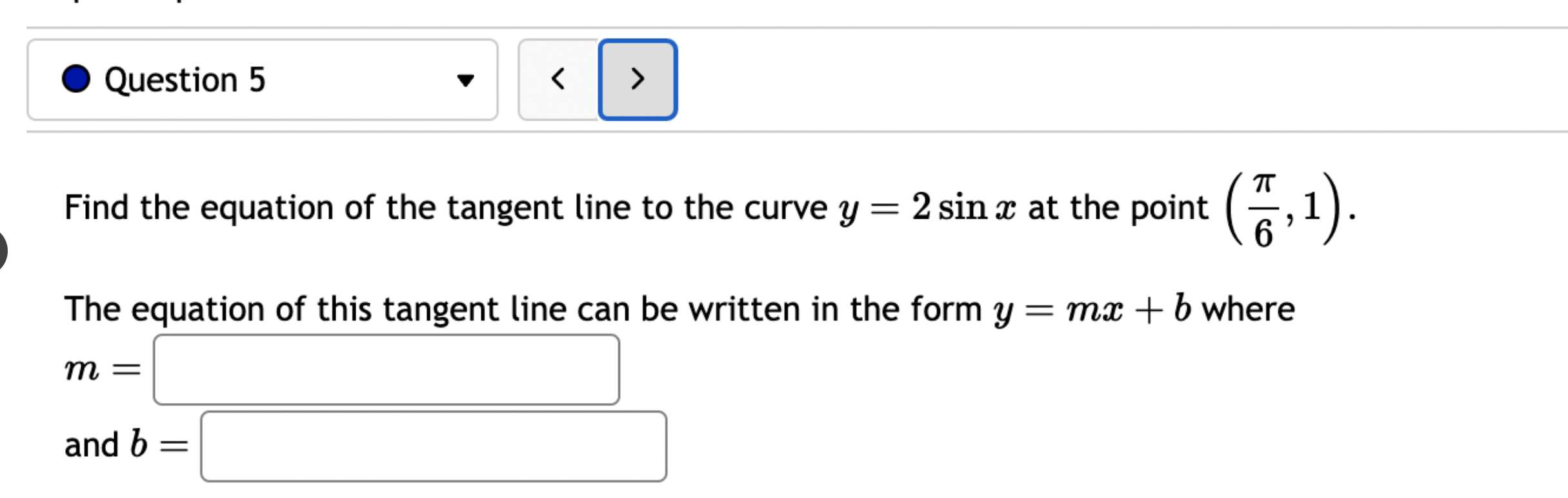
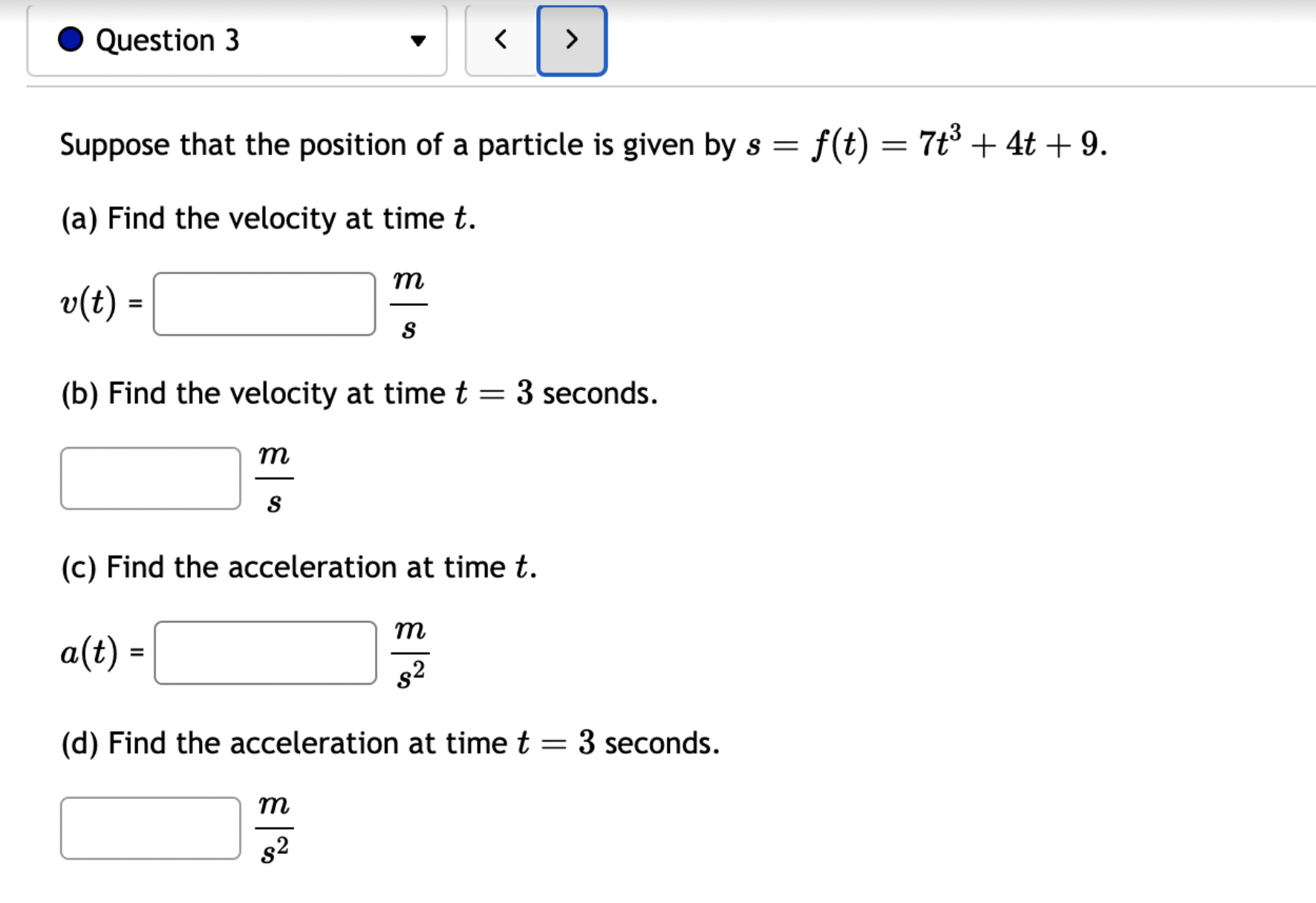
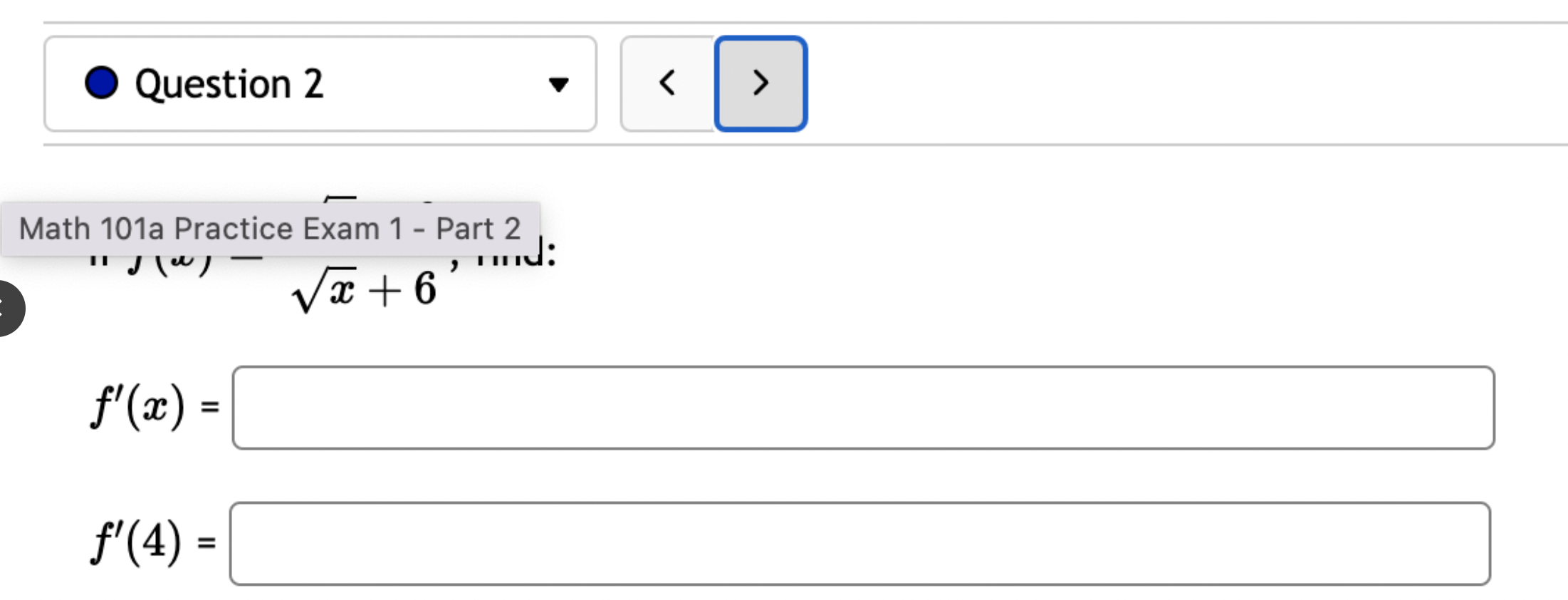
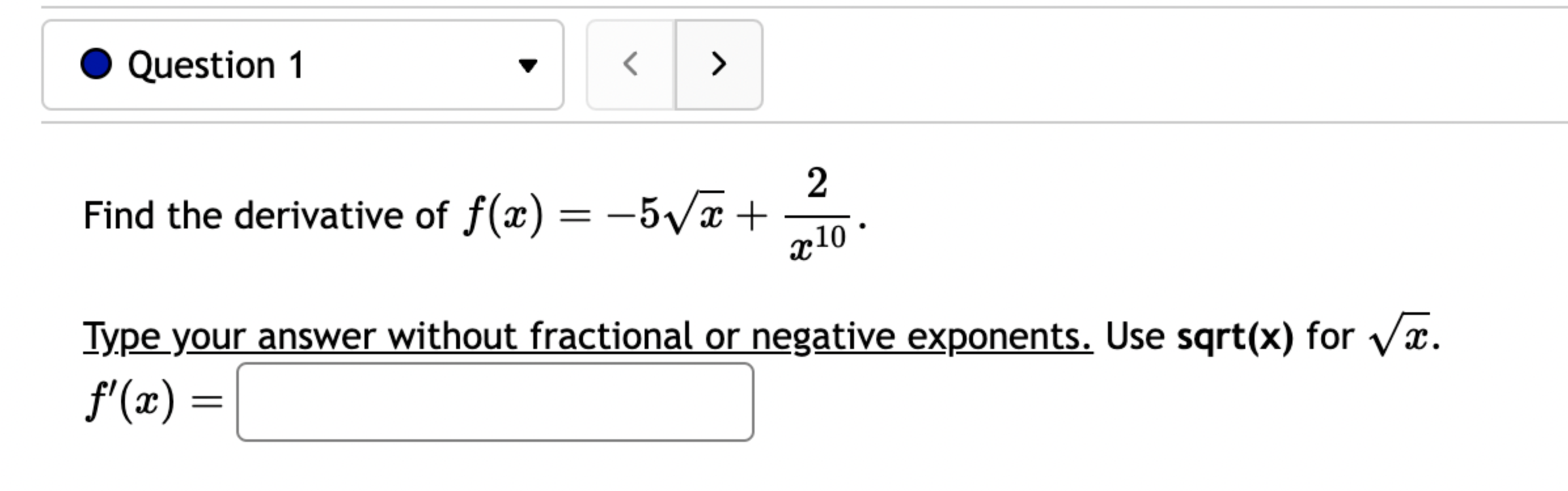
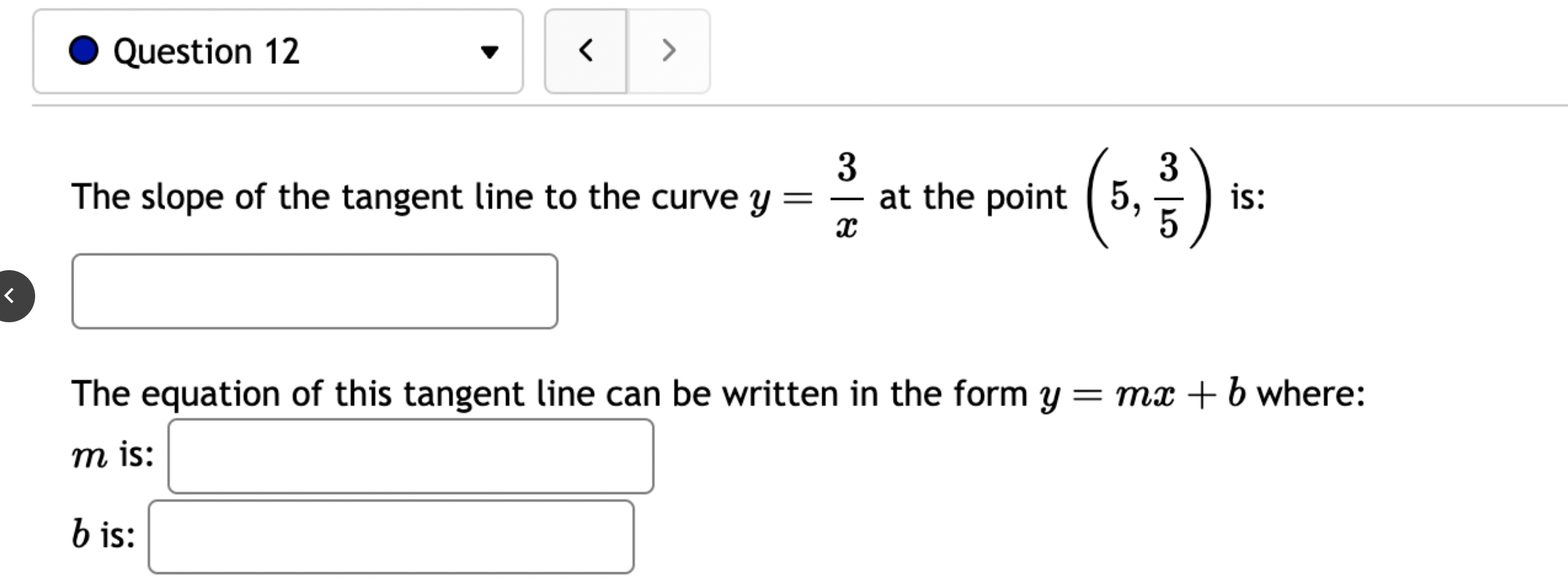
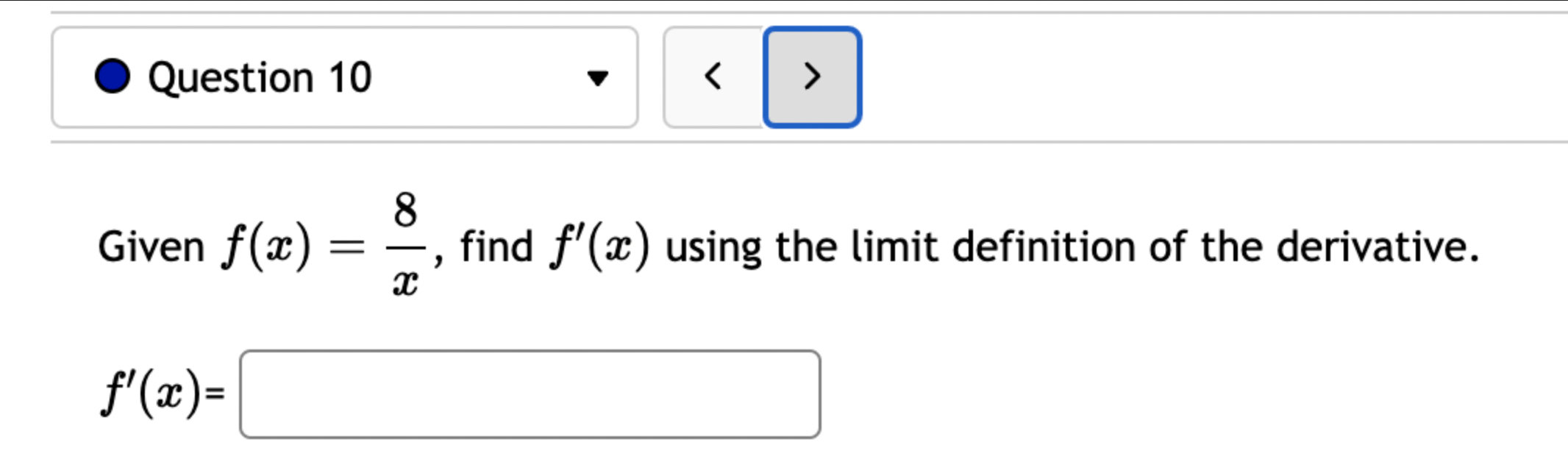
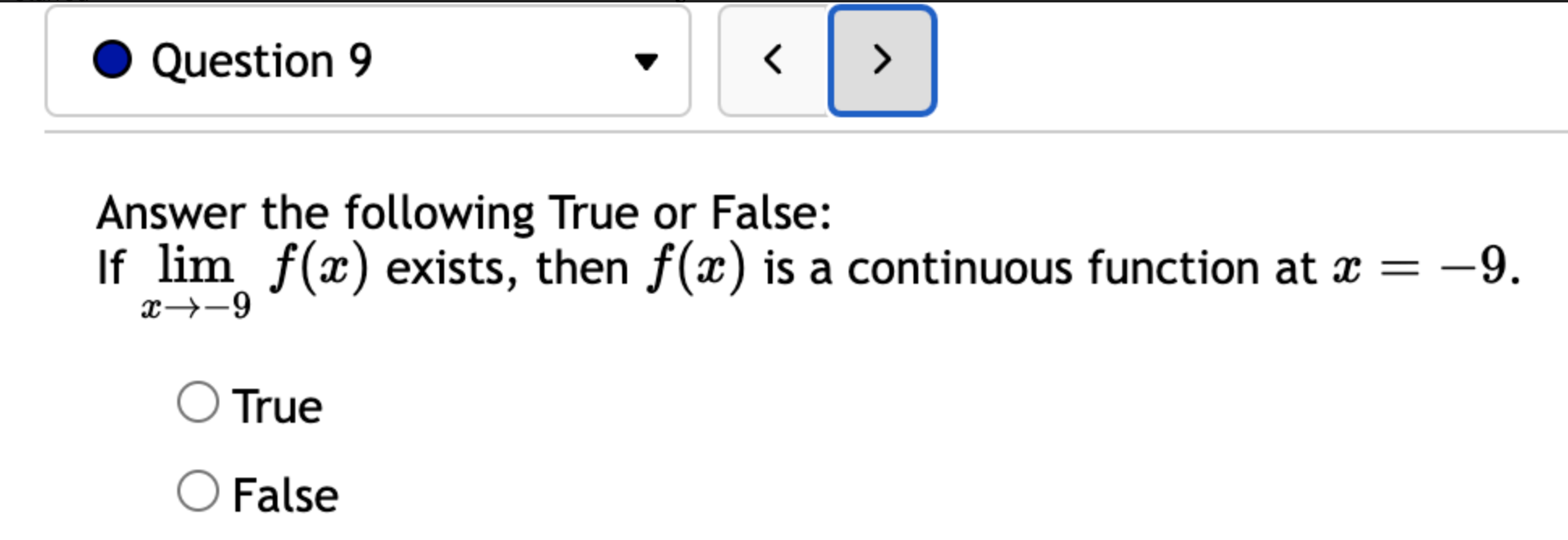
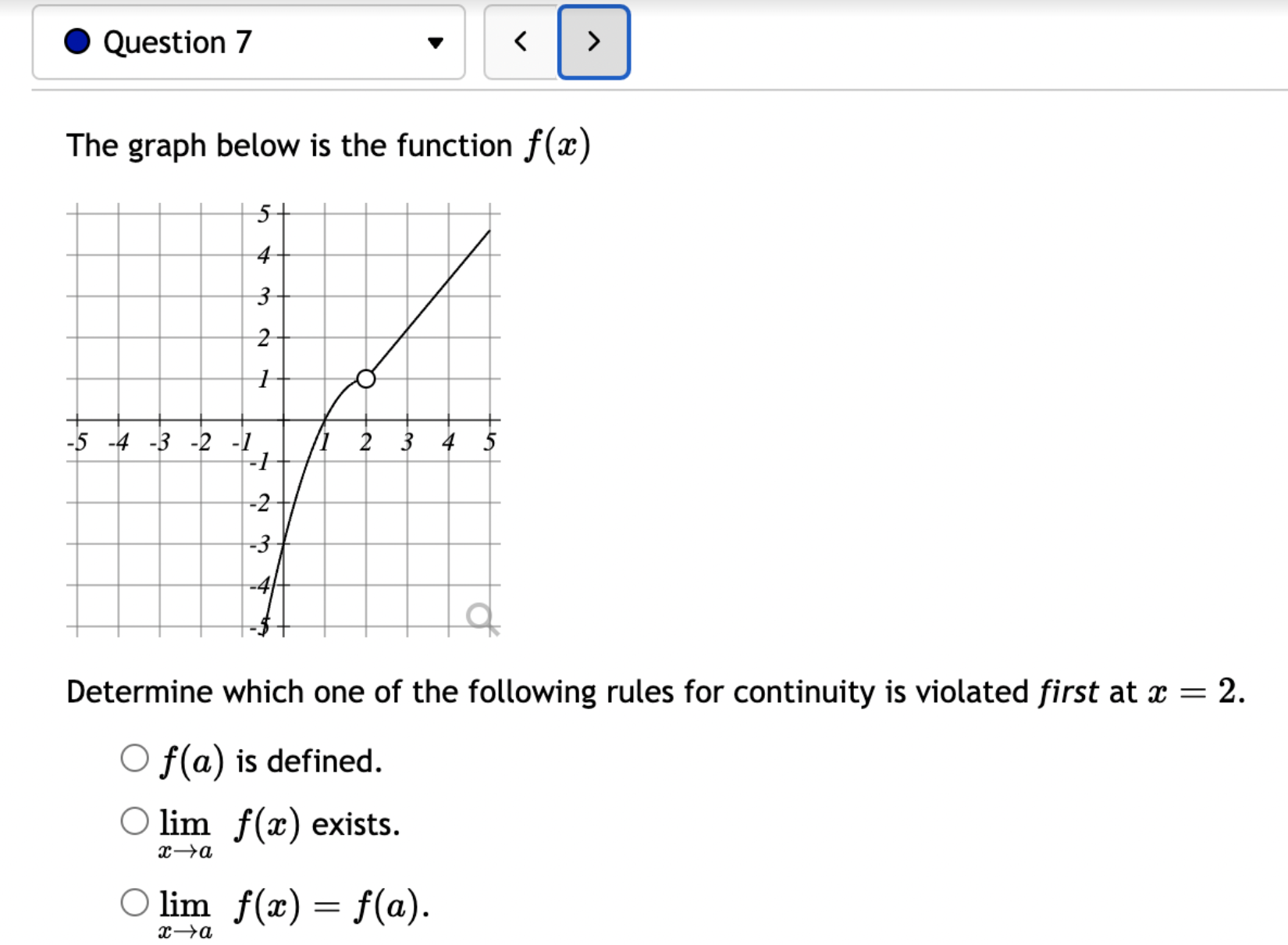
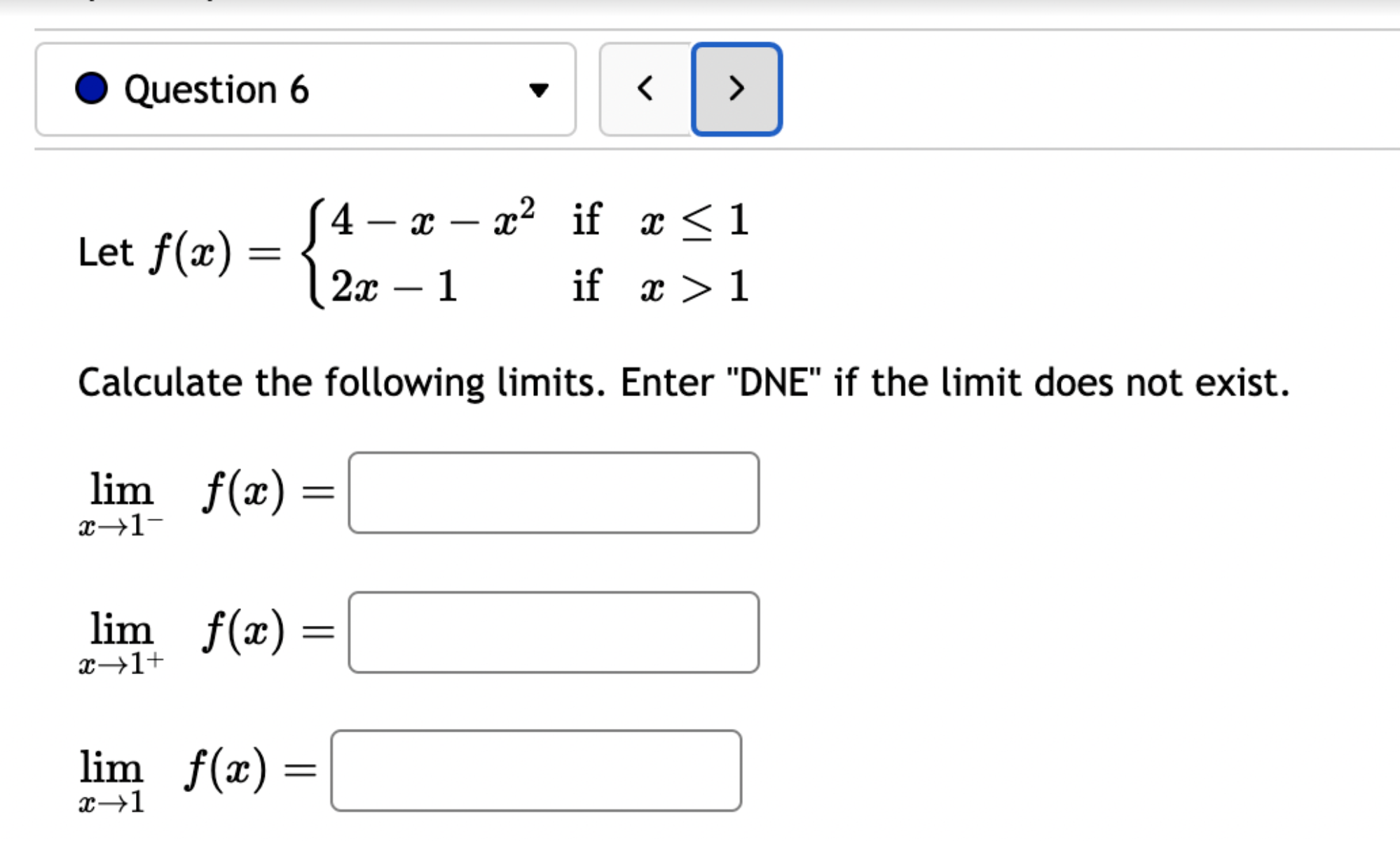
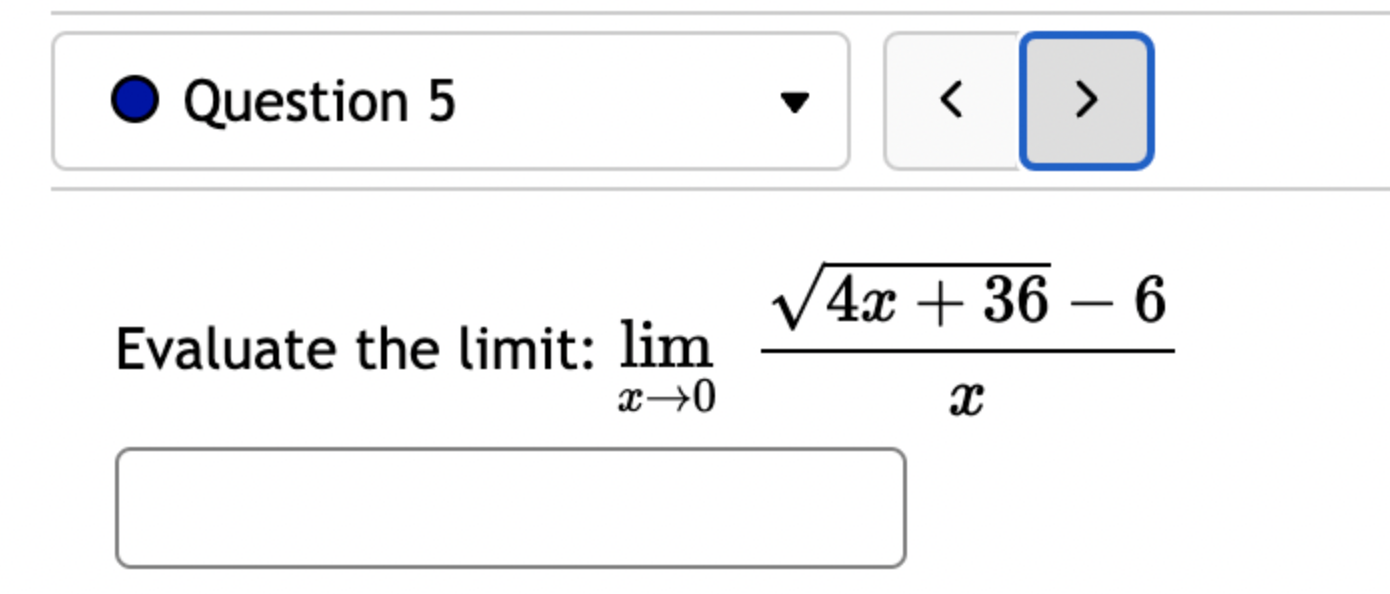
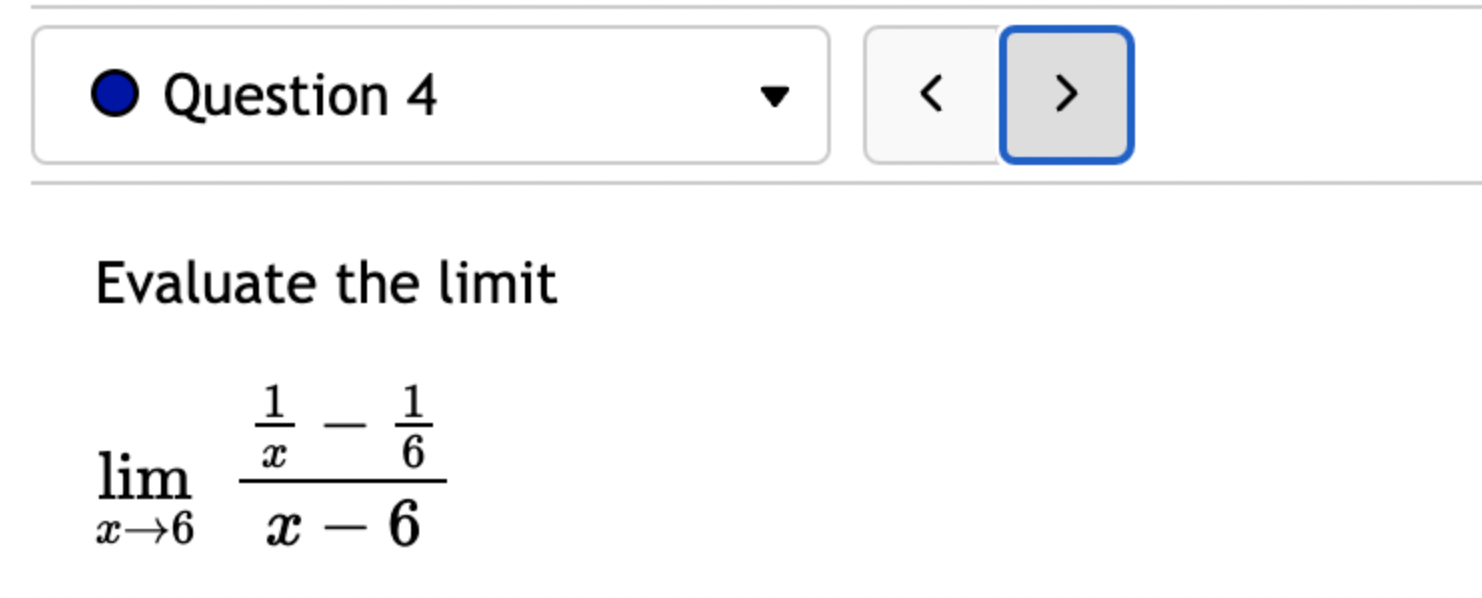
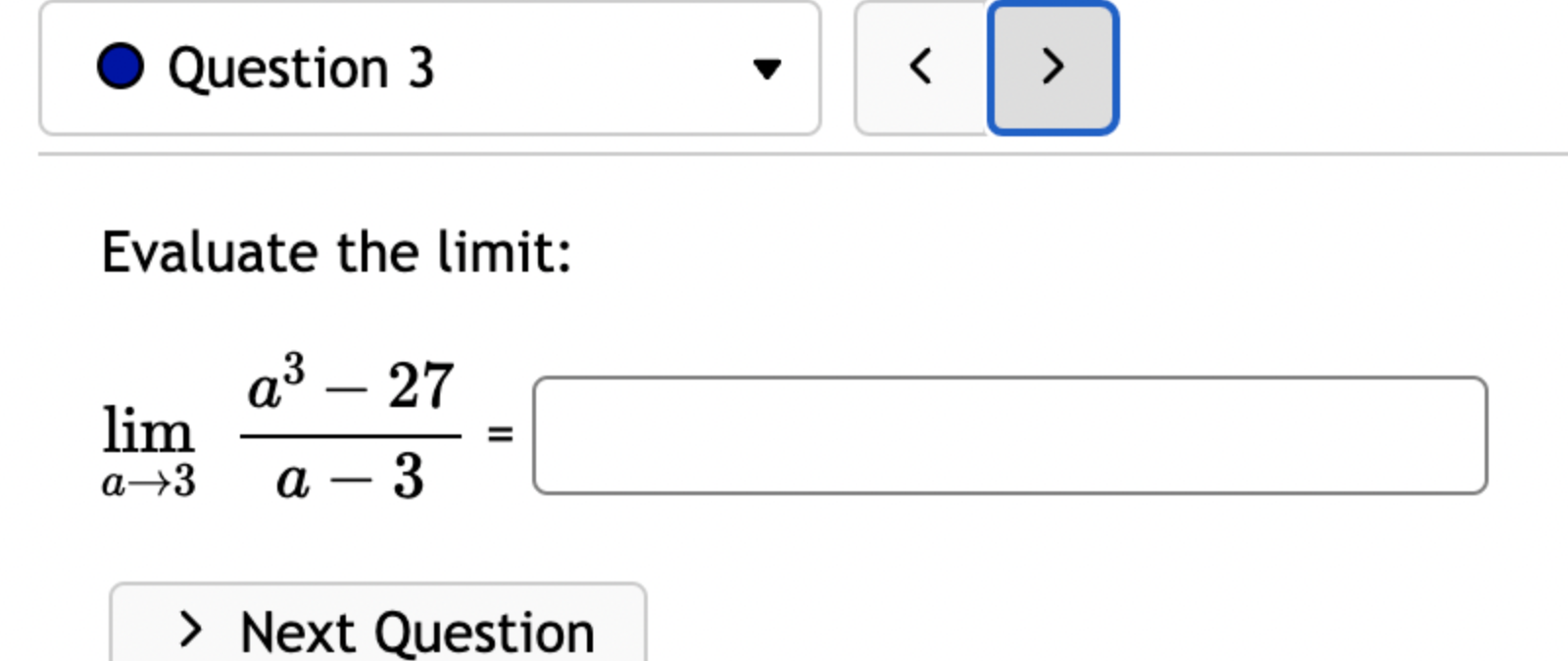
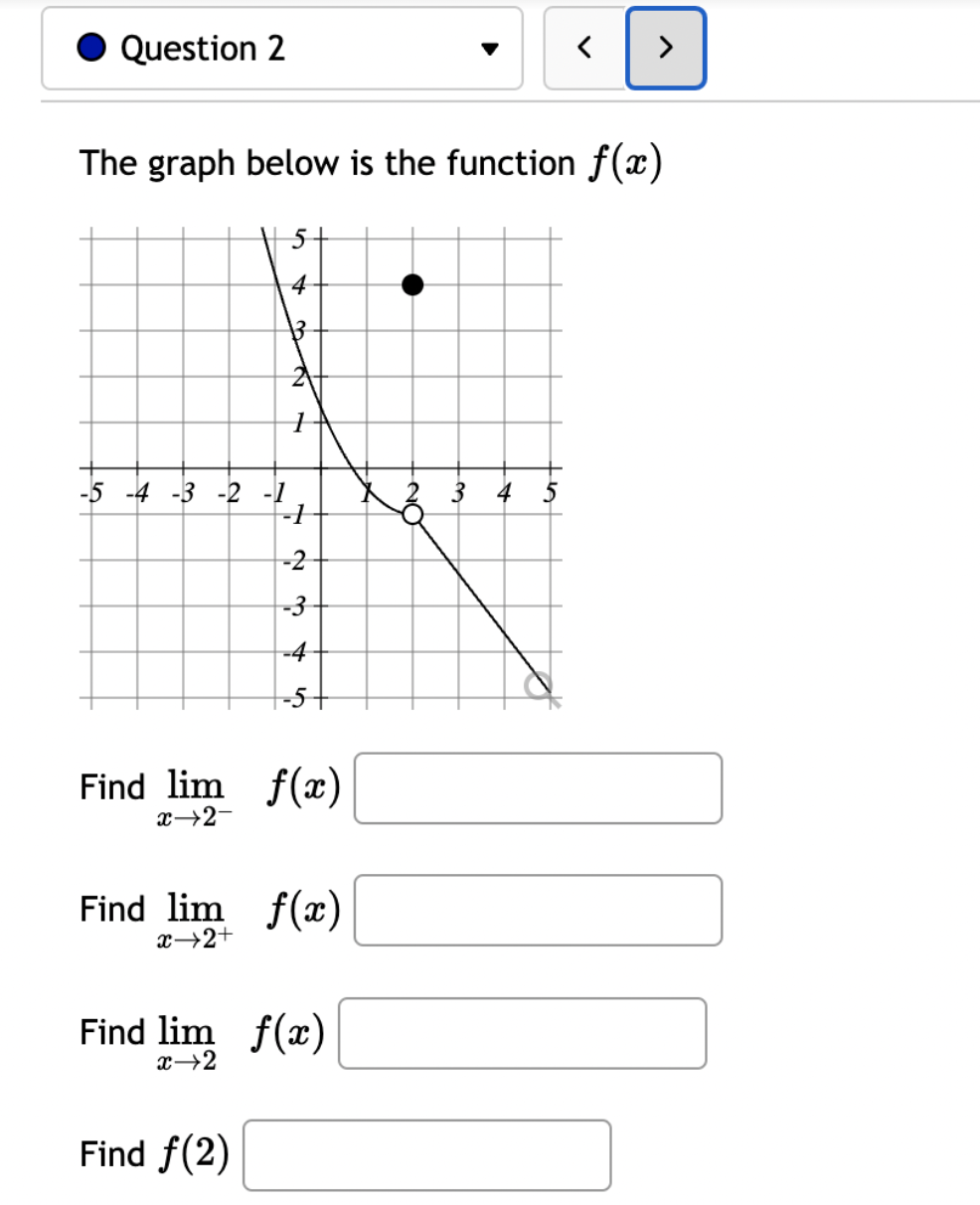
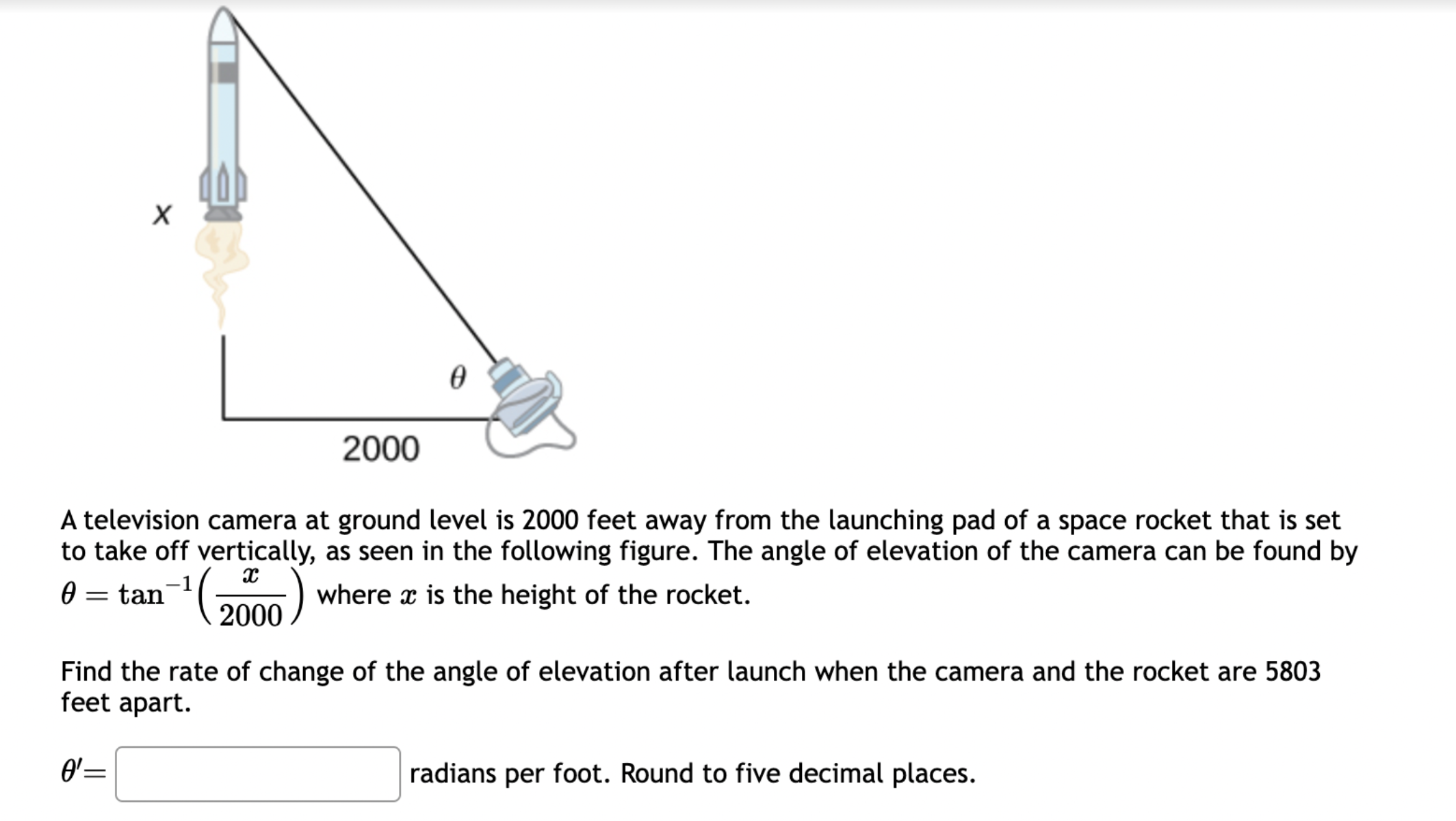
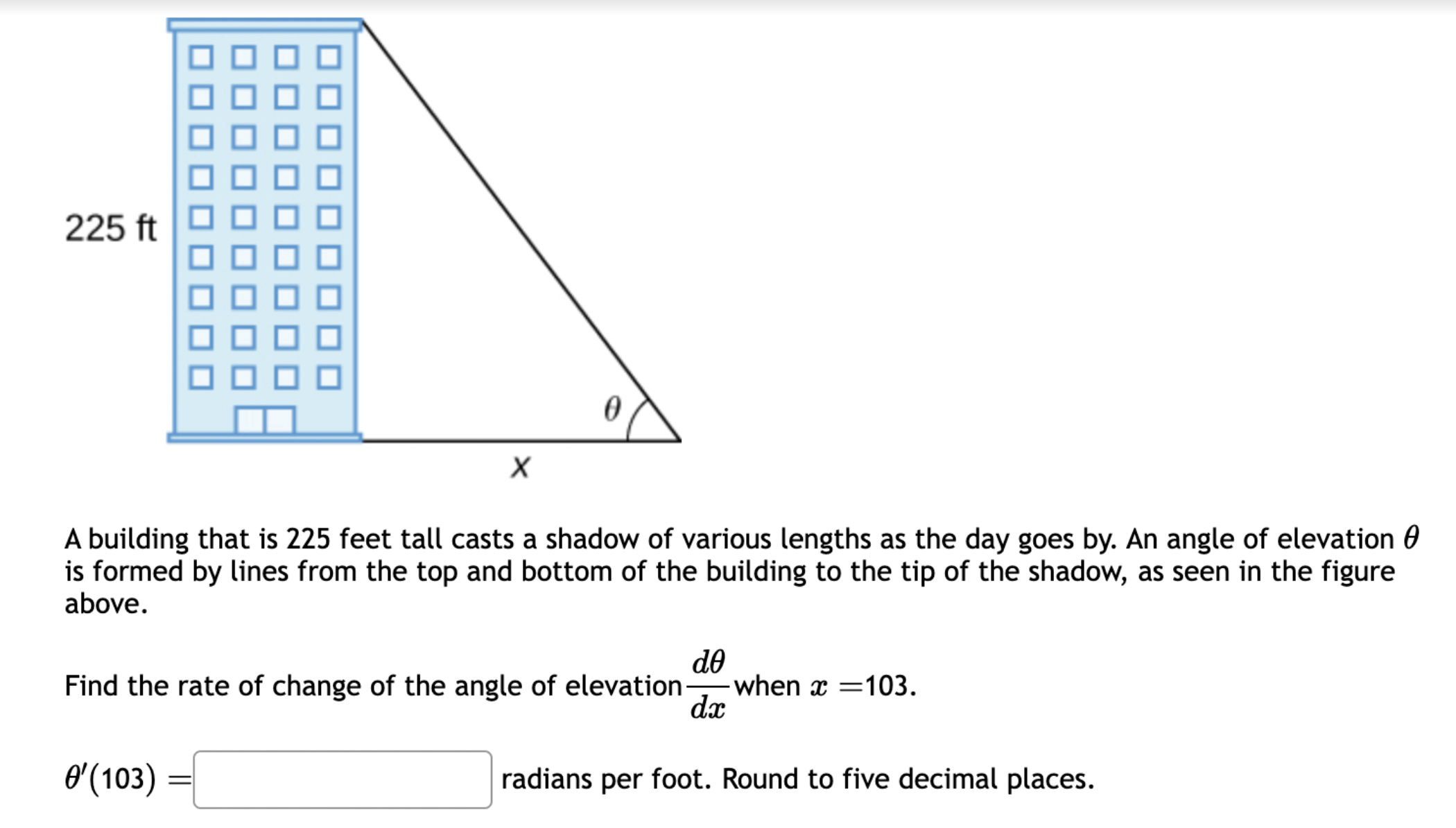
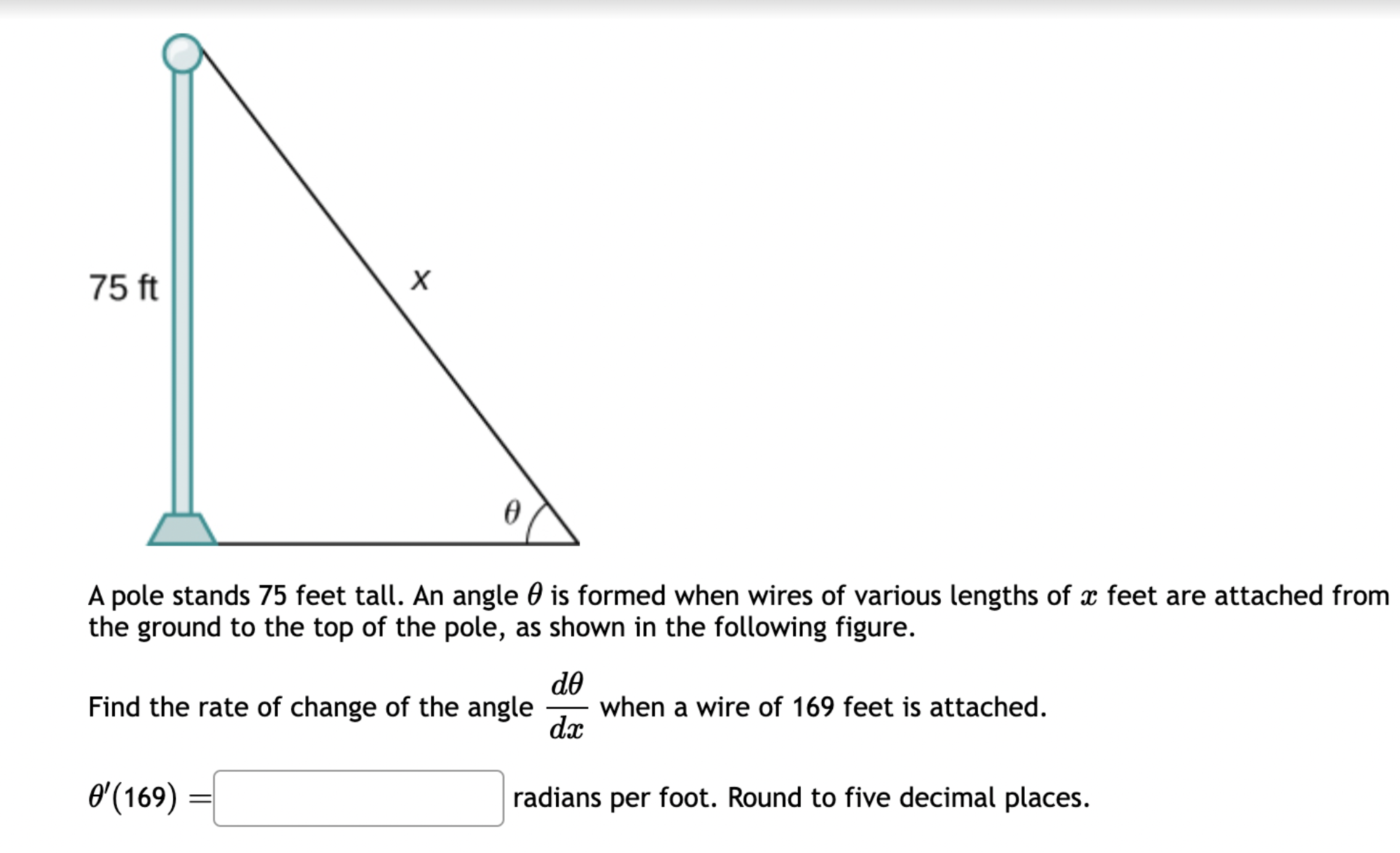
Let f(x) = '(x) = 1 (5x+3x+4)7 Let (x) = x5 . '(x) = x +3 x + 5 5 Find the derivative of: -3(sin(6x)). Let f(x) = -5 sec (7x) f'(x) = Question 8 If (x) = (2x + 4), find '(x). Find f'(1). Question 7 If (x) = '(x) = '(3) = tan x 3 - sec x 4 < > The depth (in feet) of water at a dock changes with the rise and fall of tides. The depth is modeled by the function s ( = + 5T ) - t 6 6 D(t) = 3 cos +5 where t is the number of hours after midnight. Find the rate at which the depth is changing at 5 a.m. Round your answer to 4 decimal places. ft/hr Question 5 < and b = = > Find the equation of the tangent line to the curve y = 2 sin at the point (,1). The equation of this tangent line can be written in the form y = mx + b where m Question 3 Suppose that the position of a particle is given by s = f(t) = 7t + 4t + 9. (a) Find the velocity at time t. v(t) = m S m < S (b) Find the velocity at time t = 3 seconds. m 8 > (c) Find the acceleration at time t. a(t) = m 8 (d) Find the acceleration at time t = 3 seconds. Question 2 Math 101a Practice Exam 1 - Part 2 11 Je und: x+6' '(x) = f'(4) = < > Question 1 Find the derivative of f(x) = -5x + 2 x10 Type your answer without fractional or negative exponents. Use sqrt(x) for x. '(x) = Question 12 < > The slope of the tangent line to the curve y = 3 X at the point (5, crlco is: The equation of this tangent line can be written in the form y = mx + b where: m is: b is: Question 11 < > If f(x) = 4 + 5x 3x, find '(-5). Question 10 Given f(x) '(x)= = 8 find f'(x) using the limit definition of the derivative. - < > X Question 9 6-x JC Answer the following True or False: If lim_ f(x) exists, then f(x) is a continuous function at x = 9. True False < > Question 8 Let f(x) = < [3x - 5 -7x+b if x > 9 5 if x 9 > If f(x) is a function which is continuous everywhere, then we must have b= Question 7 The graph below is the function f(x) 5+ 4 3 2 1 -5 -4 -3 -2 -1 -1 -2 -3 1 2 3 4 5 < > Determine which one of the following rules for continuity is violated first at x = 2. O f(a) is defined. O lim f(x) exists. xa Olim f(x) = f(a). xa Question 6 Let f(x) = = 4 x x if 2x 1 < lim__f(x) = lim_f(x) = [ > x1 if x > 1 Calculate the following limits. Enter "DNE" if the limit does not exist. lim__f(x) = Question 5 Evaluate the limit: lim x0 < > 4x +36-6 X Question 4 Evaluate the limit 1 X lim x6 X 1 6 | - 6 < > Question 3 Evaluate the limit: a - 27 a-3 lim a-3 > Next Question A < > Question 2 The graph below is the function f(x) 4 3 -5 -4 -3 -2 -1 -1 -2 -3 -4 -5+ Find lim f(x) x2- Find f(2) Find lim f(x) x2+ Find lim f(x) x2 > 3 Question 1 Consider f(x) = x - 25 x-5 X 4.9 4.99 4.999 4.9999 f(x) 9.9 X 5.1 5.01 5.001 Looking at the values, we can estimate that lim f(x) = x5 5.0001 f(x) 10.1 X 0 2000 A television camera at ground level is 2000 feet away from the launching pad of a space rocket that is set to take off vertically, as seen in the following figure. The angle of elevation of the camera can be found by 0 = tan -(2000) where x is the height of the rocket. Find the rate of change of the angle of elevation after launch when the camera and the rocket are 5803 feet apart. 0'= radians per foot. Round to five decimal places. 225 ft X 0 A building that is 225 feet tall casts a shadow of various lengths as the day goes by. An angle of elevation is formed by lines from the top and bottom of the building to the tip of the shadow, as seen in the figure above. 0 (103) de dx Find the rate of change of the angle of elevation- - when x 103. radians per foot. Round to five decimal places. 75 ft X A pole stands 75 feet tall. An angle is formed when wires of various lengths of x feet are attached from the ground to the top of the pole, as shown in the following figure. 0 (169) 0 Find the rate of change of the angle = de dx when a wire of 169 feet is attached. radians per foot. Round to five decimal places. Differentiate (x) = sin(5x). Use exact values. '(x) = If (x) = 7 sin(x), then '(x) = Let (x) = tan(cos(7x)) f'(x) = If f(x) = 5 tan-(6 sin(2x)), '(x) = If (x) = 6 sin(x), then f'(x) = If (x) = 5 sin(x), find '(x). Find '(0.5). If (x) = tan(5x7), find '(x). Use exact values. f'(x) = If f(t) f'(t) = = tan n(4t), find f'(t). Use exact values.