Question
Let G(x)=(x^(2)-12x+35)/(|7-x|)+|x-1| for x!=7 a) As x approaches 7 , the quotient gives an indeterminate form of the type (infty )/(infty ) infty -infty
Let
G(x)=(x^(2)-12x+35)/(|7-x|)+|x-1|for
x!=7\ a) As
xapproaches 7 , the quotient gives an indeterminate form of the type
(\\\\infty )/(\\\\infty )
\\\\infty -\\\\infty \
1^(\\\\infty )\
(0)/(0)\
0\\\\times \\\\infty \
0^(0)\ b) Using properties of absolute value, assume
x>7and simplify the expression
G(x).\ FORMATTING: Your answer should not have absolute values or a quotient\ Answer
G(x)=\ C) Compute the limit as
xgoes to 7 from the right, if it exists.\ FORMATTING: If the limit doesn't exist, write diverges.\
\\\\lim_(x->7^(+))G(x)=\ (A)\ d) Simplify the expression for
G(x)when
1.\ FORMATTING: Your answer should not have absolute values or a quotient\ Answer:
G(x)=\ \ e) Compute the limit as
x goes to 7 from the left, if it exists.\ FORMATTING: If the limit doesn't exist, write diverges.\
\\\\lim_(x->7^(-))G(x)=\ f) Using (c) and (e) above, compute the limit as
x goes to 7 , if it exists.\ FORMATTING: if the limit doesnt exist, write diverges.\
\\\\lim_(x->7)G(x)= 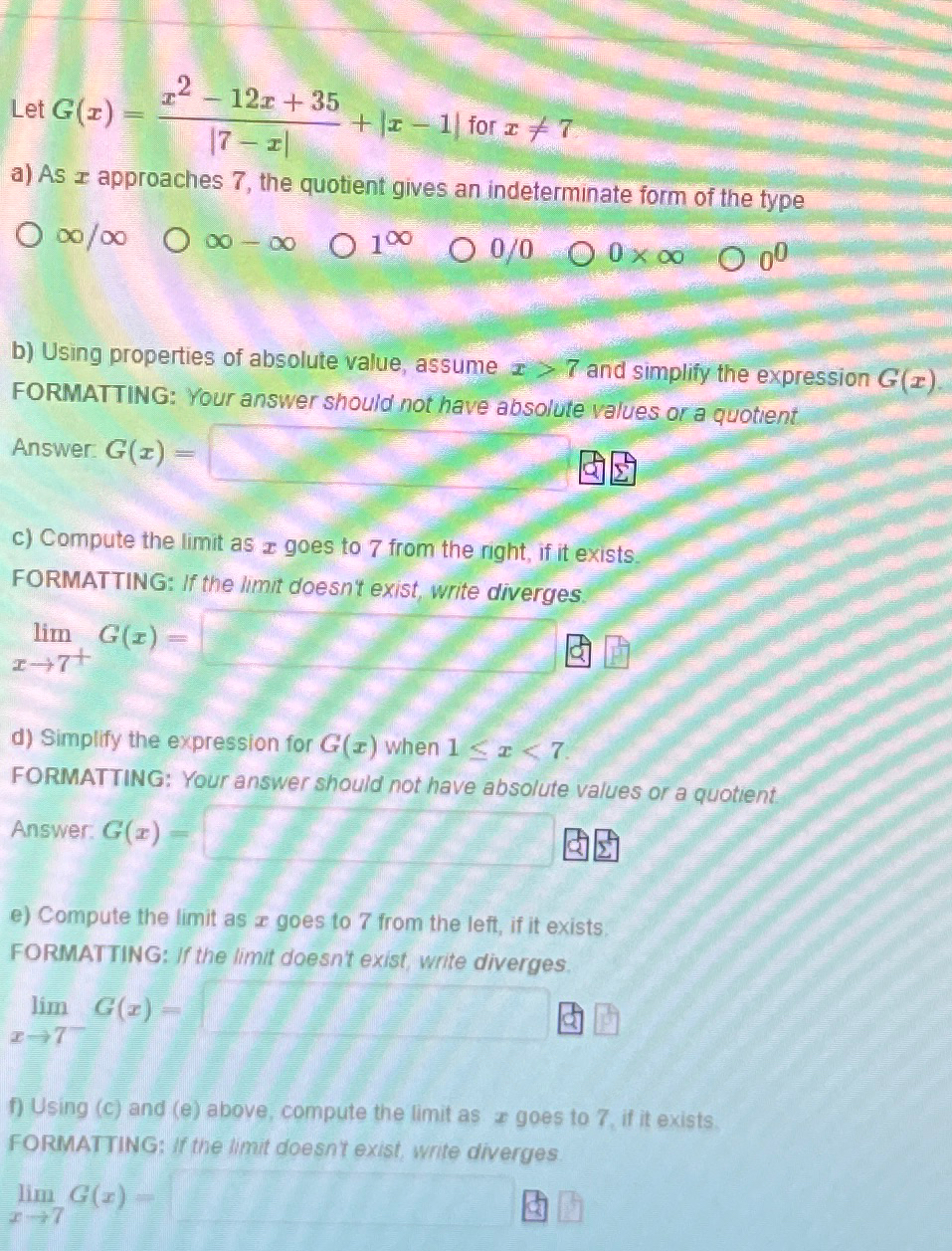
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


