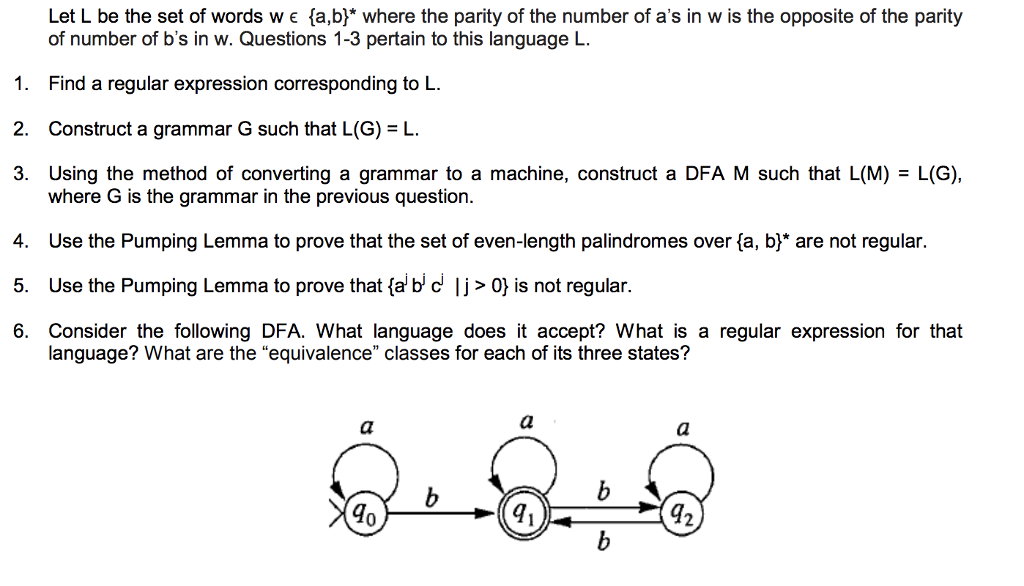
Let L be the set of words w E {a,b)" where the parity of the number of a's in w is the opposite of the parity of number of b's in w. Questions 1-3 pertain to this language L 1. Find a regular expression corresponding to L 2. Construct a grammar G such that L(G) . 3. Using the method of converting a grammar to a machine, construct a DFA M such that L(M) - L(G), where G is the grammar in the previous question. 4. Use the Pumping Lemma to prove that the set of even-length palindromes over (a, b* are not regular. 5. Use the Pumping Lemma to prove that fa b c lj> 0 is not regular. 6. Consider the following DFA. What language does it accept? What is a regular expression for that language? What are the "equivalence" classes for each of its three states? Let L be the set of words w E {a,b)" where the parity of the number of a's in w is the opposite of the parity of number of b's in w. Questions 1-3 pertain to this language L 1. Find a regular expression corresponding to L 2. Construct a grammar G such that L(G) . 3. Using the method of converting a grammar to a machine, construct a DFA M such that L(M) - L(G), where G is the grammar in the previous question. 4. Use the Pumping Lemma to prove that the set of even-length palindromes over (a, b* are not regular. 5. Use the Pumping Lemma to prove that fa b c lj> 0 is not regular. 6. Consider the following DFA. What language does it accept? What is a regular expression for that language? What are the "equivalence" classes for each of its three states