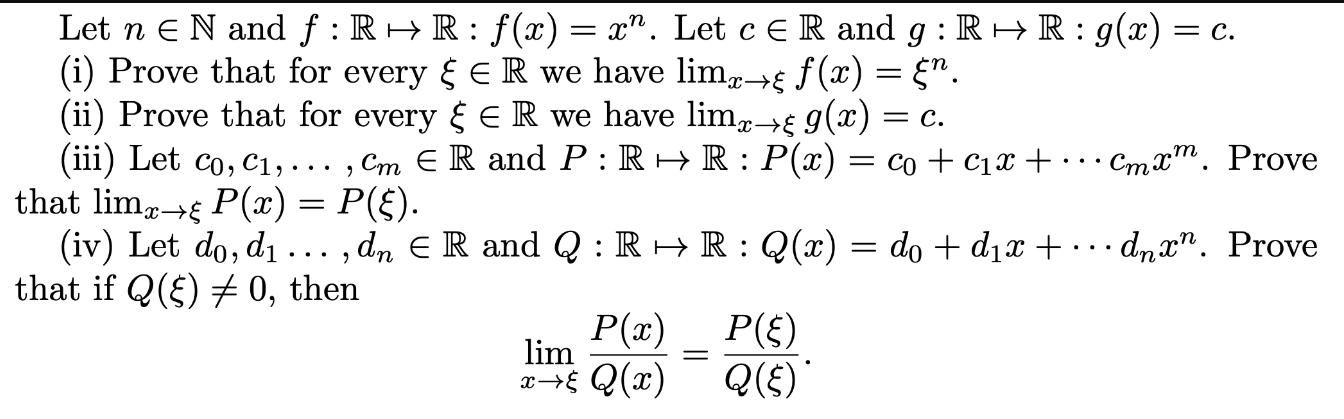
Let n E N and f:RR: f(x)= x^. Let c R and g: R R: g(x) = c. (i) Prove that for every & E R we have limxg f(x) = . (ii) Prove that for every & E R we have limxg g(x) = = C. (iii) Let co, C,..., Cm E R and P: RR: P(x) = co + cx + that lim P(x) = P(). (iv) Let do, d..., dn E R and Q: R R: Q(x) = do + dx + that if Q() # 0, then P(x) lim x Q(x) P(E) Q() Cmx. Prove dnxn. Prove