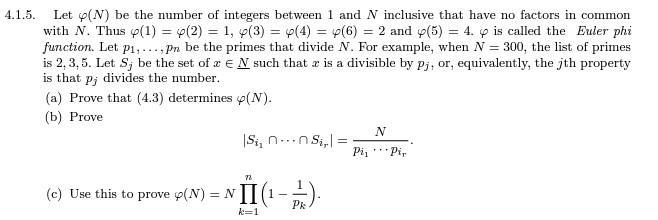
Let p(N) be the number of integers between 1 and N inclusive that have no factors in common with N. Thus p(1) = p(2) = 1, p(3) = y(4) = p(6) = 2 and p(5) = 4. p is called the Euler phi function. Let p1,..., Pn be the primes that divide N. For example, when N = 300, the list of primes is 2, 3, 5. Let S; be the set of e E N such that a is a divisible by pj, or, equivalently, the jth property is that p; divides the number. 4.1.5. (a) Prove that (4.3) determines o(N). (b) Prove |Si, n..n Si, Pi, %3D *** Pir (c) Use this to prove p(N) = N||(1 Pk k=1