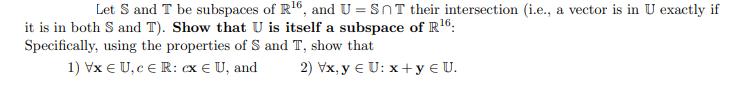
Let S and T be subspaces of R6, and U=SnT their intersection (i.e., a vector is in U exactly if it is in both S and T). Show that U is itself a subspace of R6. Specifically, using the properties of S and T, show that 1) VxE U, c R: cx U, and 2) Vx, y EU: x + y U.