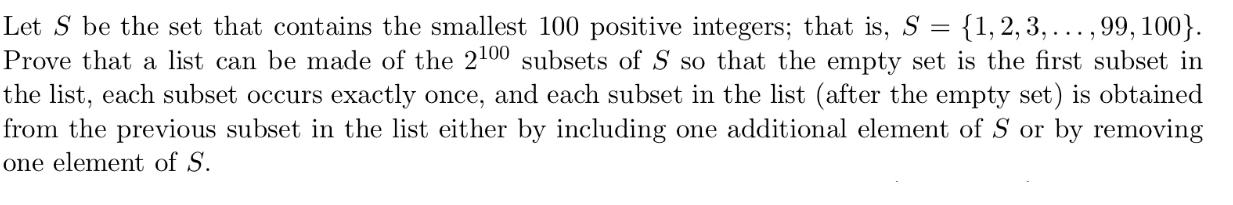
Let S be the set that contains the smallest 100 positive integers; that is, S = {1, 2, 3, ... , 99, 100}. Prove that a list can be made of the 2100 subsets of S so that the empty set is the first subset in the list, each subset occurs exactly once, and each subset in the list (after the empty set) is obtained from the previous subset in the list either by including one additional element of S or by removing one element of S.