Answered step by step
Verified Expert Solution
Question
1 Approved Answer
1. Let X be a Banach space and let T be a bounded linear operator on X. Show that if ||T|| < 1, then
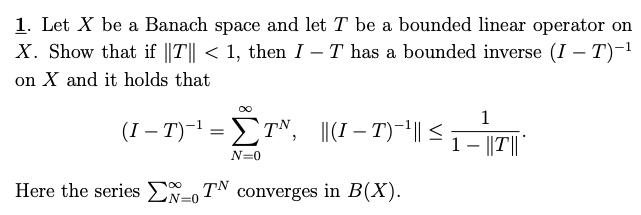
1. Let X be a Banach space and let T be a bounded linear operator on X. Show that if ||T|| < 1, then I - T has a bounded inverse (I-T)- on X and it holds that 0 1 (I T)- = TN, ||(I - T) -`' || 1 - ||T|| | N=0 Here the series o TN converges in B(X). N=0
Step by Step Solution
★★★★★
3.34 Rating (160 Votes )
There are 3 Steps involved in it
Step: 1
Solution let X be T let operator IT II 1 then inverse IT tha...
Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2
Step: 3
Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started
Essentials Of Business Statistics
Authors: Bruce Bowerman, Richard Connell, Emily Murphree, Burdeane Or
5th Edition
978-1259688867, 1259688860, 78020530, 978-0078020537
