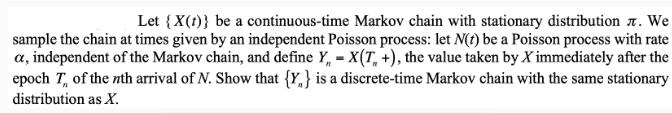
Let {X(t)} be a continuous-time Markov chain with stationary distribution. We sample the chain at times given by an independent Poisson process: let N(t) be a Poisson process with rate a, independent of the Markov chain, and define Y, = X(T +), the value taken by X immediately after the epoch T, of the nth arrival of N. Show that {Y} is a discrete-time Markov chain with the same stationary distribution as X.