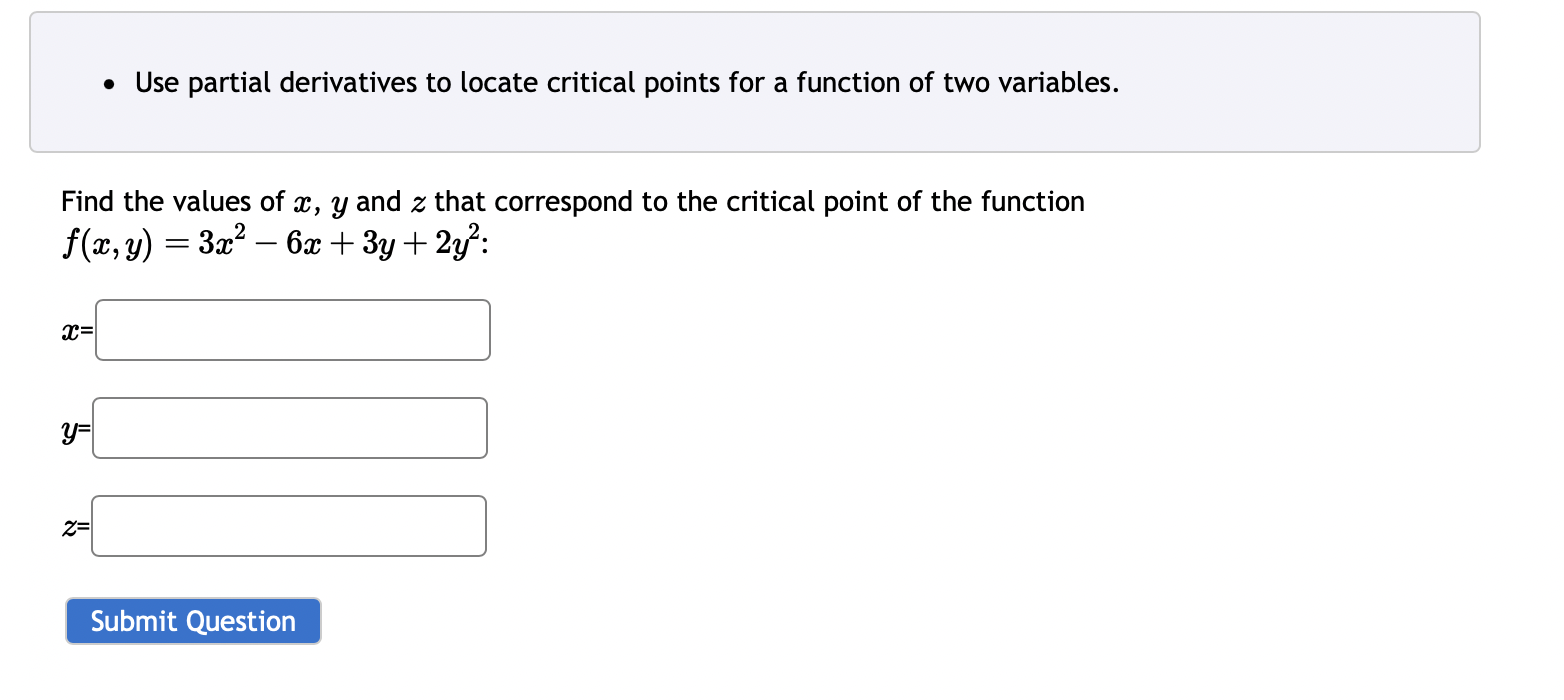
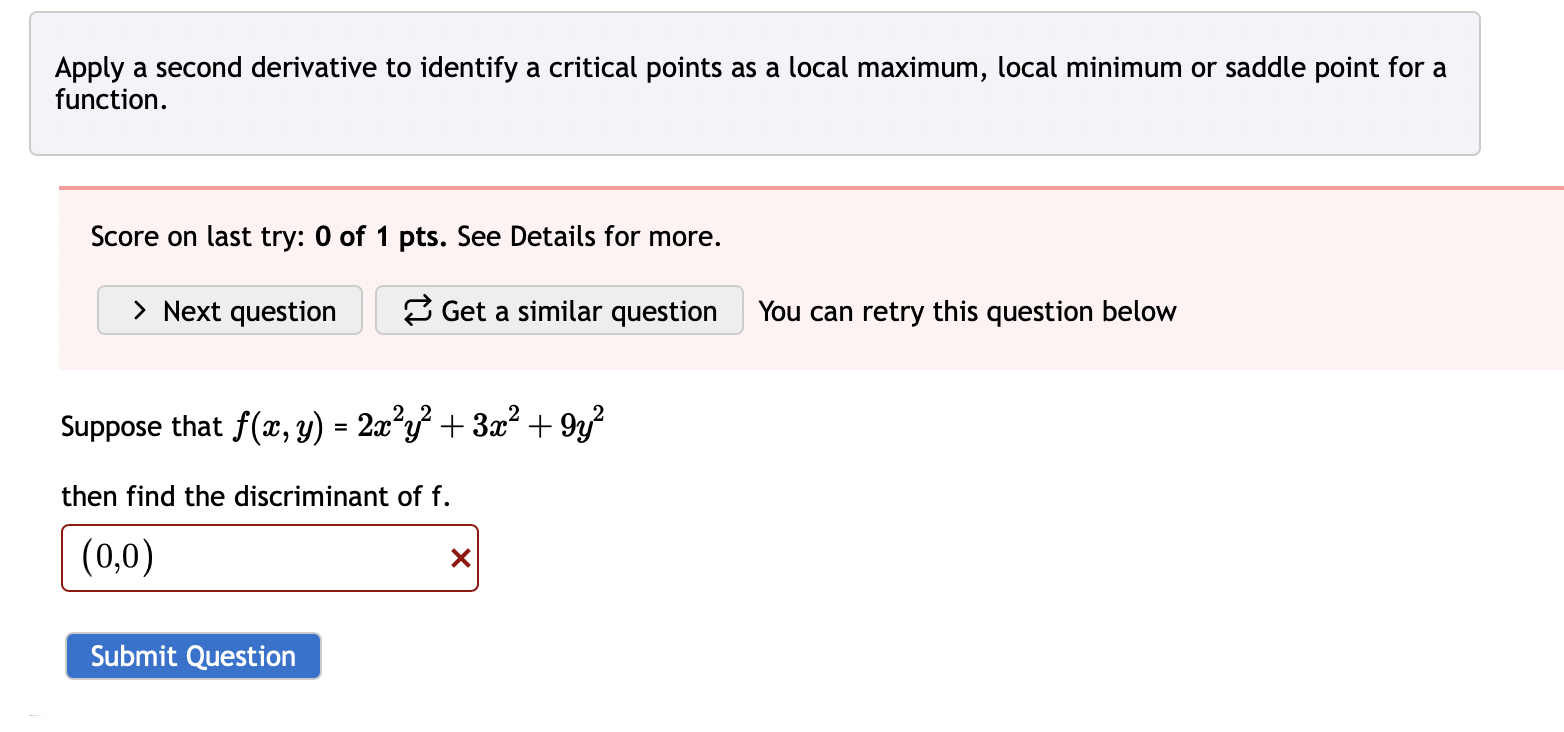
Let z(x, y) = 8x + 7y where x = 3s - 7t & y = 9s - 9t. z s s t & and using the chain rule. t Calculate z s one. z t one. || II z s & t 48x + 126y by first finding -112x - 126y X syntax error. Check your variables you might be using an incorrect X syntax error. Check your variables - you might be using an incorrect Find the values of x, y and z that correspond to the critical point of the function f(x, y) = 3x 6x + 3y + 2y: x= y= Use partial derivatives to locate critical points for a function of two variables. Z= Submit Question Find the values of x, y and z that correspond to the critical point of the function: 3x + 4x - 2y + 4y 1xy f(x, y) = = Enter your answer as a decimal number, or a calculation (like 22/7). x= y= Use partial derivatives to locate critical points for a function of two variables. Z= Question Help: Video 2= (Round to 4 decimal places) (Round to 4 decimal places) (Round to 4 decimal places) Find the values of x, y and z that correspond to the critical point of the function: f(x,y) = 2x + 3x 8y + 4y Enter your answer as a number (like 5, -3, 2.2) or as a calculation (like 5/3, 2^3, 5+4). x= y= Use partial derivatives to locate critical points for a function of two variables. Z= Question Help: Video Apply a second derivative to identify a critical points as a local maximum, local minimum or saddle point for a function. Score on last try: 0 of 1 pts. See Details for more. > Next question Get a similar question You can retry this question below Suppose that f(x, y) = 2xy + 3x +9y then find the discriminant of f. (0,0) Submit Question X