linear equation

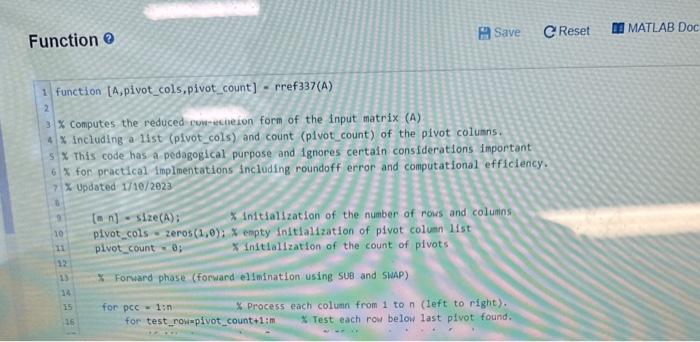
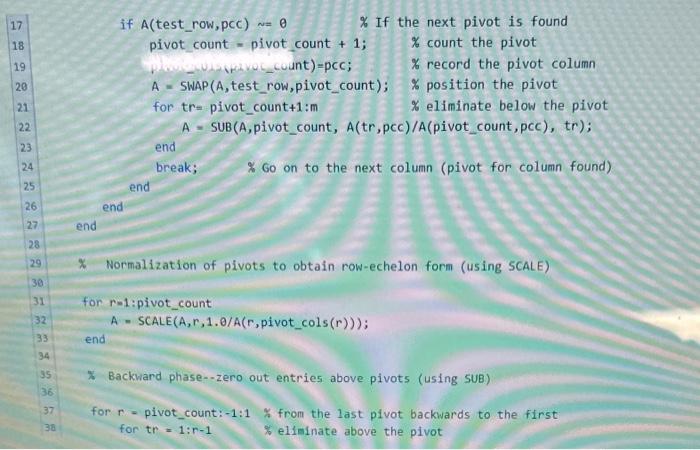
what corrections you need i have the pictures posted

MATLAB Assignment 2 (S23): Operation Counts for Gauss-Jordan Modity rref337 1. to have the imeine rref 337 count, 2. to retum additionally the mumber of floating point addition and subtraction operations performed: 3. to refurn additionaly the number of foating point multiplication and division operations performed finction TA pivot_cols.pivot_countaddsub, muldiv] = met337count(A) function [A,pivot_cols, pivot_count] = rref 337(A) X Computes the reduced ruw-scieion form of the input matrix (A) X. Including a list (pivot_cols) and count (pivot_count) of the pivot columis. X This code has a pedagogical purpose and ignores certain considerations important X for practical. Implmentations including roundoff error and computational efficiency. * updated 1/10/2023 [m,n]=size(A);x initialization of the number of rois and coluinins plvot_cols = zeros (1,0);& empty initlalization of plvot coluan list plvot count =0; Xinitlalization of the count of pivots Forward phase (forward elimination using suB and SWAP) for pce =1:n X Process each columin from 1 to (left to r ight), for test_rouipivot_countitim . Test each row belou last plvot found. if A (test_row, pCc) =0 \% If the next pivot is found pivot count = pivot count +1;% count the pivot 1._._. % record the pivot column A=SWAP(A, test_row,pivot_count); \% position the pivot for tr= pivot_count t+1:m% eliminate below the pivot A=SUB(A, pivot_count, A(tr,pcc)/A(pivot_count,pCc),tr); end break; \% Go on to the next column (pivot for column found) end end end \% Normalization of pivots to obtain row-echelon form (using SCALE) for r=1 :pivot_count A - SCALE (A,r,1./A(r, pivot__ols (r))); end * Backward phase--zero out entries above pivots (using SUB) for r - pivot_count:-1:1 \& from the last pivot backwards to the first for tr=1:r1 \% eliminate above the pivot \[ A=\operatorname{SUB}(A, r, A(t r, \text { pivot_cols }(r)), t r) ; \] end end end 45% Subfunctions performing row operations 47 function A=SuB(A,p, multiplier, q) 49 \% Row q is replace by row q minus multiplien times Row P 50 A(q,:)=A(q,i) - multiplier* A(p,:); 51 end 52 function A=SWAP(A,p,q) 54.X Exchanges row p and row q of the matrix A 55 temp_row =A(p1:); A(p,:)=A(q,:); A(q1:)= temp_row: end function A - SCALE (A,p, multiplier ) Code to cali your function ? 1 A A=[123;456;789] [RREF, pivot_cols, pivot_count, addsub, muldiv] =rref337c(A) Your code tested with A=[123;456;789] (Pretest) Your code tested with A=[123456;456789;789101112 Your code tested on an undisclosed 510 matrix (no pretest) MATLAB Assignment 2 (S23): Operation Counts for Gauss-Jordan Modity rref337 1. to have the name rref 337 count, 2. 10 retum additionally the number of foating point addition and subtraction operations performed. 3. to retum additionally the number of floating point mutipbcation and division operations performed. function [A.pivot_cols pivot_count addsub,muldiv] = rref337 count (A) function [A,pivot_cols, pivot_count ]= rref337(A) $ computes the reduced row-echelon form of the input matrix (A) 7 including a list (pivot_cols) and count (pivot_count) of the pivot columns. 7 This code has a pedagogical purpose and ignores certain considerations important * for practical implmentations including roundoff error and computational efficiency. Updated 1/10/223 [mn]=size(A); initialization of the number of rows and columns pivot_cols = zenos (1,); empty initialization of pivot column list pivot_count =0; initialization of the count of pivots * Forward phase (forward elimination using SUB and SWAP) for pce =1:n& Process each colunn from 1 to n (left to right). for test_row-pivot_count+1:m Test each row below last pivot found. for test row-pivot_count+1:m Test each row below last pivot found. If A( test_row, pCC ) =. If the next pivot is found pivot_count = pivot_count +1; count the pivot pivot_cols(pivot_count)=pcc; \% record the pivot column A=SNAP(A, test_row, pivot_count );% position the pivot for tr= pivot_count +1:m% eliminate below the pivot A=SUB(A, pivot_count, A(tr,pcc)/A(pivot_count,pcc),tr); end break; % co on to the next column (pivot for column found) end end end Normalization of pivots to obtain row-echelon form (using SCALE) for r=1 :pivot_count A=SCALE(A,r,1,/A(r,pivot_cols(r))); end 7 Backward phase-zero out entries above pivots (using suB) X Subfunctions performing row operations function A=SUB(A,p, nultiplier,q) 7 Row q is replace by row q minus multiplier times Row p A(q,:)=A(q,:)-multiplier*A(p,i); end function A=SWAP(A,p,q) 54 Exchanges row p and row q of the matrix A \[ \begin{array}{ll} 55 & \text { temp_row }=A\left(p_{1}:: ight) ; \\ 56 & A\left(p_{3}: ight)=A(q,:) ; \\ 57 & A(q,:)=\text { temp_row; } \end{array} \] end function A=SCALE(A,p, multiplier ) \% Multiplies row p by multiplier 62A(p,:)= multiplier* A(p,:); 63 end Code to call your function ? Assessment: Your code tested with A=[1 23;456;789] (Prefest) Your code tested with A=[123456;456789;7891011 12] (Pretest) Your code tested on an undisclosed 510 matrix (no prefest) MATLAB Assignment 2 (S23): Operation Counts for Gauss-Jordan Modity rref337 1. to have the imeine rref 337 count, 2. to retum additionally the mumber of floating point addition and subtraction operations performed: 3. to refurn additionaly the number of foating point multiplication and division operations performed finction TA pivot_cols.pivot_countaddsub, muldiv] = met337count(A) function [A,pivot_cols, pivot_count] = rref 337(A) X Computes the reduced ruw-scieion form of the input matrix (A) X. Including a list (pivot_cols) and count (pivot_count) of the pivot columis. X This code has a pedagogical purpose and ignores certain considerations important X for practical. Implmentations including roundoff error and computational efficiency. * updated 1/10/2023 [m,n]=size(A);x initialization of the number of rois and coluinins plvot_cols = zeros (1,0);& empty initlalization of plvot coluan list plvot count =0; Xinitlalization of the count of pivots Forward phase (forward elimination using suB and SWAP) for pce =1:n X Process each columin from 1 to (left to r ight), for test_rouipivot_countitim . Test each row belou last plvot found. if A (test_row, pCc) =0 \% If the next pivot is found pivot count = pivot count +1;% count the pivot 1._._. % record the pivot column A=SWAP(A, test_row,pivot_count); \% position the pivot for tr= pivot_count t+1:m% eliminate below the pivot A=SUB(A, pivot_count, A(tr,pcc)/A(pivot_count,pCc),tr); end break; \% Go on to the next column (pivot for column found) end end end \% Normalization of pivots to obtain row-echelon form (using SCALE) for r=1 :pivot_count A - SCALE (A,r,1./A(r, pivot__ols (r))); end * Backward phase--zero out entries above pivots (using SUB) for r - pivot_count:-1:1 \& from the last pivot backwards to the first for tr=1:r1 \% eliminate above the pivot \[ A=\operatorname{SUB}(A, r, A(t r, \text { pivot_cols }(r)), t r) ; \] end end end 45% Subfunctions performing row operations 47 function A=SuB(A,p, multiplier, q) 49 \% Row q is replace by row q minus multiplien times Row P 50 A(q,:)=A(q,i) - multiplier* A(p,:); 51 end 52 function A=SWAP(A,p,q) 54.X Exchanges row p and row q of the matrix A 55 temp_row =A(p1:); A(p,:)=A(q,:); A(q1:)= temp_row: end function A - SCALE (A,p, multiplier ) Code to cali your function ? 1 A A=[123;456;789] [RREF, pivot_cols, pivot_count, addsub, muldiv] =rref337c(A) Your code tested with A=[123;456;789] (Pretest) Your code tested with A=[123456;456789;789101112 Your code tested on an undisclosed 510 matrix (no pretest) MATLAB Assignment 2 (S23): Operation Counts for Gauss-Jordan Modity rref337 1. to have the name rref 337 count, 2. 10 retum additionally the number of foating point addition and subtraction operations performed. 3. to retum additionally the number of floating point mutipbcation and division operations performed. function [A.pivot_cols pivot_count addsub,muldiv] = rref337 count (A) function [A,pivot_cols, pivot_count ]= rref337(A) $ computes the reduced row-echelon form of the input matrix (A) 7 including a list (pivot_cols) and count (pivot_count) of the pivot columns. 7 This code has a pedagogical purpose and ignores certain considerations important * for practical implmentations including roundoff error and computational efficiency. Updated 1/10/223 [mn]=size(A); initialization of the number of rows and columns pivot_cols = zenos (1,); empty initialization of pivot column list pivot_count =0; initialization of the count of pivots * Forward phase (forward elimination using SUB and SWAP) for pce =1:n& Process each colunn from 1 to n (left to right). for test_row-pivot_count+1:m Test each row below last pivot found. for test row-pivot_count+1:m Test each row below last pivot found. If A( test_row, pCC ) =. If the next pivot is found pivot_count = pivot_count +1; count the pivot pivot_cols(pivot_count)=pcc; \% record the pivot column A=SNAP(A, test_row, pivot_count );% position the pivot for tr= pivot_count +1:m% eliminate below the pivot A=SUB(A, pivot_count, A(tr,pcc)/A(pivot_count,pcc),tr); end break; % co on to the next column (pivot for column found) end end end Normalization of pivots to obtain row-echelon form (using SCALE) for r=1 :pivot_count A=SCALE(A,r,1,/A(r,pivot_cols(r))); end 7 Backward phase-zero out entries above pivots (using suB) X Subfunctions performing row operations function A=SUB(A,p, nultiplier,q) 7 Row q is replace by row q minus multiplier times Row p A(q,:)=A(q,:)-multiplier*A(p,i); end function A=SWAP(A,p,q) 54 Exchanges row p and row q of the matrix A \[ \begin{array}{ll} 55 & \text { temp_row }=A\left(p_{1}:: ight) ; \\ 56 & A\left(p_{3}: ight)=A(q,:) ; \\ 57 & A(q,:)=\text { temp_row; } \end{array} \] end function A=SCALE(A,p, multiplier ) \% Multiplies row p by multiplier 62A(p,:)= multiplier* A(p,:); 63 end Code to call your function ? Assessment: Your code tested with A=[1 23;456;789] (Prefest) Your code tested with A=[123456;456789;7891011 12] (Pretest) Your code tested on an undisclosed 510 matrix (no prefest)