Question: make a project on topic priority queue using binary heap help with the research paper giving above to implementation code in python data structure do











make a project on topic priority queue using binary heap help with the research paper giving above to implementation code in python data structure do it in one day
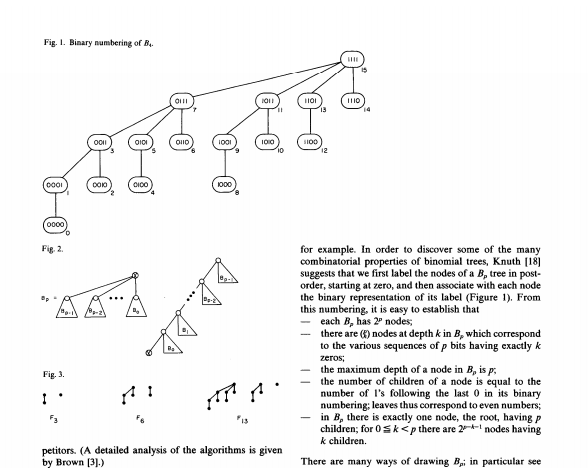
S.L. Graham, R.L. Rivest Editors Programming Techniques A Data Structure for Manipulating Priority Queues Jean Vuillemin Universit de Paris-Sud A data structure is described which can be used for representing a collection of priority queues. The primitive operations are insertion, deletion, union, update, and search for an item of earliest priority. Key Words and Phrases: data structures, implementation of set operations, priority queues, mergeable heaps, binary trees CR Categories: 4.34, 5.24, 5.25, 5.32, 8.1 A priority queue is a set; each element of such a set has a name, which is used to uniquely identify the element, and a label or priority drawn from a totally ordered set. Elements of the priority queue can be thought of as awaiting service, where the item with the smallest label is always to be served next. Ordinary stacks and queues are special cases of priority queues. A variety of applications directly require using prior ity queues: job scheduling, discrete simulation languages where labels represent the time at which events are to occur, as well as various sorting problems. These are discussed, for example, in (2, 3, 5, 11, 15, 17, 24). Priority queues also play a central role in several good algorithms, such as optimal code constructions, Chartre's prime number generator, and Brown's power series multipli- cation (see [16] and [17]); applications have also been found in numerical analysis algorithms [10, 17, 19) and in graph algorithms for such problems as finding shortest paths 12, 13) and minimum cost spanning tree [2, 4, 25). Typical applications require primitive operations among the following five: INSERT, DELETE, MIN, UP- DATE, and UNION. The operation INSERT (name, label, Q) adds an element to queue Q, while DELETE (name) removes the element having that name. Operation MIN (Q) returns the name of the element in Q having the least label, and UPDATE (name, label) changes the label of the element named. Finally, UNION (Q... Q.) merges into Q, all elements of Q, and Q.: the sets Q, and Q, become cmpty. In what follows, we assume that names are handled in a separate dictionary (2, 17) such as a hash- table or a balanced tree. If deletions are restricted to elements extracted by MIN, such an auxiliary symbol table is not needed. The heap, a truly elegant data structure discovered by J. W. Williams and R. W. Floyd, handles a sequence of n primitives INSERT, DELETE, and MIn, and runs in O(nlogn) elementary operations using absolutely mini- mal storage [17]. For applications in which UNION IS necessary, more sophisticated data structures have been 1. Introduction In order to design correct and efficient algorithms for solving a specific problem, it is often helpful to describe our first approach to a solution in a language close to that in which the problem is formulated. One such language is that of set theory, augmented by primitive set manipulation operations. Once the algorithm is out lined in terms of these set operations, one can then look for data structures most suitable for representing each of the sets involved. This choice depends only upon the collection of primitive operations required for each set. empty. In what follows, we assume that names are In order to design correct and efficient algorithms for handled in a separate dictionary (2, 17) such as a hash- solving a specific problem, it is often helpful to describe table or a balanced tree. If deletions are restricted to our first approach to a solution in a language close to elements extracted by MIN, such an auxiliary symbol that in which the problem is formulated. One such table is not needed. language is that of set theory, augmented by primitive The heap, a truly elegant data structure discovered set manipulation operations. Once the algorithm is out- by J. W. Williams and R. W. Floyd, handles a sequence lined in terms of these set operations, one can then look of n primitives INSERT, DELETE, and MIN, and runs in for data structures most suitable for representing each of (rlogn) elementary operations using absolutely mini- the sets involved. This choice depends only upon the mal storage [17]. For applications in which UNION IS collection of primitive operations required for each set. necessary, more sophisticated data structures have been It is thus important to establish a good catalogue of such devised, such as 2-3 trees (2.17), leftist trees (5, 17), and data structures. A summary of the state of the art on this binary heaps [91. question can be found in (2). In this paper, we add to The data structure we present here handles an arbi- this catalogue a data structure which allows efficient trary sequence of n primitives, each drawn from the five manipulation of priority queues. described above, in O(nlogr) machine operations and O(n) memory cells. It also allows for an efficient treat- ment of a large number of updates, which is crucial in connection with spanning tree algorithms: Our data structure provides an implementation (described in [25]) of the Cheriton-Tarjan-Yao (3) minimum cost span- General permission to make fair use in teaching or research of all or part of this material is granted to individual readers and to nonprofit ning tree algorithm which is much more straightforward libraries acting for them provided that ACM's copyright notice is given than the original one. and that reference is made to the publication, to its date of issue, and to the fact that reprinting privileges were granted by permission of the The proposed data structure uses less storage than Association for Computing Machinery. To otherwise reprint a figure, leftist, AVL, or 2-3 trees; in addition, when the primitive table, other substantial excerpt, or the entire work requires specific operations are carefully machine coded from the pro- permission as does republication, or systematic or multiple reproduc grams given in Section 4, they yield worst case running Author's address: Laboratoire de Recherche en Informatique, times which compare favorably with those of their com- Bt. 490, Universit de Paris-Sud, Centre d'Orsay 91405Orsay, We assume here that indexing through the symbol table is done 1978 ACM 0001-0782/78/0400-0309 500,75 in constant time. 309 April 1998 Lion France Communications Fig. L. Binary numbering of B4 III HII 1110 11 13 14 OONI QIC 1001 IDIO 10 SIOO 12 0001 DOID 0100 1000 0000 D Fig. 2 444 for example. In order to discover some of the many combinatorial properties of binomial trees, Knuth [18] suggests that we first label the nodes of a B, tree in post- order, starting at zero, and then associate with each node the binary representation of its label (Figure 1). From this numbering, it is easy to establish that each B. has 2' nodes there are (1) nodes at depth k in B, which correspond to the various sequences of p bits having exactly k zeros: the maximum depth of a node in B, is ps the number of children of a node is equal to the number of i's following the last 0 in its binary numbering: leaves thus correspond to even numbers: in B, there is exactly one node, the root, having P children, for 0 Sk
0 is either empty or is a labeled binomial tree B, There are three operands at each step of the algorithm which play identical roles, cach operand is either empty or a labeled binomial tree B. One of the operands is the carry, and the other two are the ith components of F. and F. respectively. If all three operands are empty, the ing of n items is represented by a labeled binomial forest F.: Each item (name, label) is stored in a different node of F, subject to the constraint that, if node i is a child of nodej in F., the labels A, and of the items respectively associated must satisfy 12. This is called the "heap condition" by Knuth [17), and it arises through the natural contraction" of perfect tournaments as shown in Figures 4(a) and (b). Such a labeled binomial forest will be called a binomial queue. We now describe how to perform the UNION of two binomial queues F, and F. First consider the special case n-x-2', in which each priority queue is repre- sented by a single labeled binomial tree, say B. for F. and B/ for F.. The resulting forest B-UNION (B. B') also consists of a single labeled binomial tree with 21*1 = + nodes, defined as At each step of the algorithm a carry is propagated: the initial carry is empty, and the carry into the ith step for i> 0 is either empty or is a labeled binomial tree B, There are three operands at each step of the algorithm which play identical roles, cach operand is either empty or a labeled binomial tree B. One of the operands is the carry, and the other two are the ith components of F. and F. respectively. If all three operands are empty, the ith component of the result UNION (F.F.) is empty, as is the carry propagated to the next step. If exactly one operand is nonempty, it constitutes the ih component of the result, and the carry is empty. If two operands are nonempty, they are coupled according to the procedure described earlier in order to constitute the (+1 )th carry, the ith component of the result is empty. When all three operands are nonempty, one of them arbitrarily consti- tutes the ith component of the result, and the remaining two are coupled in order to form the carry. The proce dure starts at the oth step and stops when either For F, has been exhausted and no carry is propagated any further. The algorithm is pictured with n = 7 and n' = 5 (Figure 5). By considering a single item as constituting an F binomial queue, INSERT can be treated as a special case of UNION. A forest F, is naturally constructed as the Communications April 1978 of Volume 21 the ACM Number 4 B.- if the label of the root of B;' is smaller than the corre- sponding label in B, and B:+1- 311 Fig. 5. (a) Binary addition of 7 and 5. (b) Scheme for UNION (F. Fs). (c) Actual example. 512 900 503 170 509 0 0-0 0-0 154 0-0 0-0 0-0 0-0 426 653 ITO 154 509 CARRY 275 897 908 509 426 900 653 908 170 509 87 512 275 897 908 503 - 653 result of a sequence of N INSERT operations. The number of comparisons required by this construction is equal, on the one hand, to the number of carries propagated in the addition 1 + 1 + ... + 1 (n times), and, on the other hand, to the number of edges in the graph of F, If (n) denotes the number of ones in the binary decomposition of n, this last number is clearly equal to n-on). It follows that F. is constructed in wn) comparisons, root of one of the components of the algorithm is slightly more complex. First, we determine the compo- nent of F, in which m lies, say B. As before, we remove B, thereby forming F, with. -- 2!. We then consider of n, this last number is clearly equal to n-n). It follows that F, is constructed in - wn) comparisons, which is in). As for UNION (n, n'), exactly n) + p') - Mn+ n') comparisons are required, which is O(login +')). In order to find the minimal label of F..we merely have to explore the roots of the binomial trees composing F. and keep the name of a node having minimal label among these. This involves (n) - comparisons, which is of log n). In many applications, DELETE is restricted to extract- ing the item m found by MIN. Let B, be the labeled binomial tree in F, of which m is the root. We first remove B. from F. thus forming a labeled binomial forest Fr, with n =R-2'. Then the root of B, is cut. As we can see from Figure 2, what remains is a "complete" forest F, with n = 21 1. One then calls UNION (FF) in order to restore F. in O(log n) compari- sons again. This procedure is described in the example shown in Figure 6. If the item m to be removed by DELETE is not the B. If mis in B... we start constructing F., = (B) and decompose B by the same technique, otherwise, we further decompose B and let F include B. This continues until m becomes the root of the subtree B, to be decomposed. It is then "out" from B, thus leaving a complete Fy... which is added to the binomial queue F.,- (B-, B-2 ... B) already constructed in order to form a complete F... This forest is then merged with F., by using the UNION procedure in order to construct the resulting F-1. This algorithm is illustrated by an example in Figure 7. As for our last primitive, UPDATE, the obvious way to realize it is to perform DELETE then INSERT in se- quence. This requires Ollogn) operations for cach UP DATE. If we have to service an arbitrary sequence of primitive operations in which min is required less often than UPDATE and DELETE, and UPDATE only causes labels to increase, there is a better way to proceed. The 312 Communications of the ACM April 1978 Volume 21 Number 4 Fig. 6. (a) Labeled Fis (b) Broken up into an F, and an Ft after re- moval of 61. (c) F-UNION (F4, F5) reconstituted. Fig. 7. (a) Labeled F(b) Broken up into an F. and an Faber removal of 170. (c) F-UNION (FF) reconstituted. 170 426 ITO 426 275 154 512 - 503 503 sos 0 procedure UPDATE does not attempt to restore the struc- ture, but merely changes the label and marks the node. The DELETE procedure proceeds in the same way, chang- ing the label to, say, + . The algorithm for MIN then becomes more complicated; it explores all binomial trees in the forest F, until finding unmarked nodes on all paths from the root of the tree to the leaves; this cuts some subtrees and the forest is then reconstructed by merging all these subtrees together with the marked nodes having labels different from + *. If y marked nodes are met, it follows (see [25]) from the properties described in Section 2 that the number of trees cut is a most pelog (n/s). If we consider an arbitrary sequence of INSERT or UNION, M UPDATE OR DELETE, and m MIN, an elementary analysis (see (25) again) shows that such a sequence is treated in at most of nlogn) + Olu) + Olulog (nm/u)) operations, which is better than the naive method for m Su. Yet another way of treating UPDATE, when labels can only decrease, is described in (14). For this purpose, we represent binomial forests as binary trees through the well known "natural corre- spondence" described in [16]: Each node has fields link and rlink such that llink points to the leftmost child of the node and rlink to the node's right sibling. This leaves some freedom for defining a node's right sibling. For the purpose of the UNION procedure, it is crucial to link small trees to larger siblings on the top level, i.e. for nodes having no parent, and to link large trees to smaller siblings on lower levels, as shown in Figure 8. We can now give a formal description of our algo- rithms in an Algol-like language. Following Knuth [16], we represent a binary tree by three arrays INFO, LLINK, and RLINK containing, respectively, the label, Ilink, and rlink of each node. The value o represents an empty pointer We first describe the UNION procedure: proc UNION (RI, NI, R2, N2) - (RI, 13): {This procedure merges the two binomial queues Fland Fyielding F" for result. Each F is represented as a binary tree; R, is a pointer to its rool, and represents the number of elements in The initial carry C is zero, Variable des points to the part of being currently constructed. Location RLINK(0) is used to keep R, and thus should be available upon calling the procedure.) (N3, CRES) (NI + N2.0.0): while (mini Ni, N2) 0) (0) de NEXTBIT (NI, N2) (11/2). [12/2]) od RLINK(RES) --if Ni then Rielse R2f R3 - RLINK [0] endproe UNION Communications April 1978 of Volume 21 4. Implementation of Binomial Forests as Binary Trees Although the above discussion is an adequate pres- entation of the priority queue primitives for a very abstract machine model decision trees for example), it does not indicate how to actually code these algorithms on a digital computer. One still has to solve some prob- lems, the first of which concerns the machine represen- tation of labeled binomial forests. 313 Fig. 8. (a) Binomial queue F. (b) Same Fas a binary tree. (c) Possible machine representation for this binary tree using array memory cells and N contain, respectively, a pointer to the root of the tree and its number of elements. 170 312 426 900 697 ITO 279 512 else (C, R2, RI, LINK(R2). RLINKERI) - (R2, RLINK(R2). RLINKTRIJ, R1, LLINK R2]) endmacro CONSTRUCTCARRY. This completes the description of UNION. We omit the description of the procedure MIN, which is straight- forward. (If very frequent uses of MIN are requested, we can keep the value of the minimal label in a special register.) As for DELETE, we simply treat EXTRACTMIN, where the element having least label is first found then re- moved. (The DELETE procedure, for which we give no formal code, is very similar. A little complication arises from the necessity of keeping and updating upward parent links.) proe EXTRACTMIN RN) - (RN): This procedure extracts from the monempty labeled binomial forest F the element having minimal label. The resulting forest f' is obtained by merging two forests Fland F which we first construct (M. PRED, P, S (R. O, R. RLINK[R]): while S0 do if INFO[S] INFO[M] then (M. PRED)--(SP), (SP) -(RLINK[S], S) od (INFO[M] is the minimal label in F) (RI, NI) -- CONSTRUCTELLINK[M]); N2N-NI-; PRED=0 then R2 RLINK[M] else (R2, RLINK(PRED]) (R. RLINK[M]: (R",N") --UNION RI, MI, R2, 12) endproe EXTRACTMIN. The procedure EXTRACTMIN uses CONSTRUCT, which transforms the binary tree representations of a B, into the binary tree representation of the complete forest Fyr- obtained by removing the root of Bi essentially, this is achieved just by reversing a list. macro CONSTRUCT RAC) + (RN, N). W RAC=0 then (RN) -(0,0) (R, SUCC, RLINK(RAC), P)-(HAC, RLINK(RAC), 0,1% while SUCCO do (R. SUCC, RLINK[SUCC), P) (SUCC, RLINK[SUCC), R. 2 x P) od; N2XP-1 1 endmacro CONSTRUCT. Here NEXTBIT stands for a fragment of program that treats the eight possible cases for the carry and the relevant component of Fland F macro NEXTBIT: BITC - if C =0 then 0 else if case (Ni mod 2, N2 mod 2, arre) 001: (C. RES, RLINK(RES))--(0, C. C) 010: PROPRES(R2) 011: PROPCARRY R2) 100: PROPRES(RI) 101: PROPCARRYIRI) 110: CONSTRUCTCARRY 111: PROPRESCRI): PROPCARRY R2) endense endmacro NEXTBIT. We then have to describe the various macro proce- dures composing NEXTBIT: macro PROPRESRK (The number of bits is odd and one of them, namely R, must be added Received June 1976; revised April 1977 (R. RES, RLINK(ESD)--(RLINK(R). R. R) endmacro PROPRES macro PROPCARRYRK [Bit R must be added to the carry and the carry propagated.) if INFOR]
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


