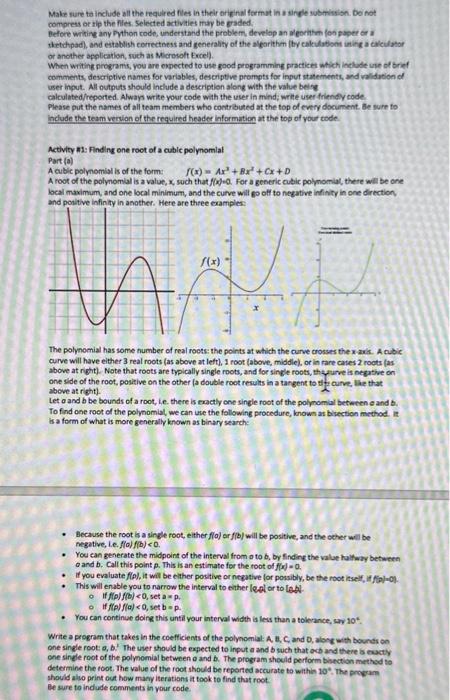
Make sure to include all the required fles in their orieina format in a single subminsion. bo not compress or tip the files, Selected activities may be eraded. Before witing any Fhthon code, understand the problem, develop an aleorhtm fos paper or a sietdpad), and establish correctees and senerality of the algarithen (thy calculationt ining a calcilator or another application, such as scrovolt Eecel). When witing progans, you are expected to use good programming practicet which inelode use of brief comments, descriptive names for variables, deseriptive prompts for input statements, and validution of user input. All outputs should include a deseription along with the value being calculated/reported. Alway write your code with the user in mind; write user friency code. Please put the names of all team members who contrbuted at the top of every document. Be sure to indude the team vesion of the required heades iaformation at the top of your code. Actlvity as: Finding one root of a cuble polynomlal Part (a) A cublic polvemial is of the form: f(x)=Ax3+8x2+Cx+D A root of the polynomal is a value, x, such that f(x)=0. For a generic cubic polmomiat, there will be one bcai maximum, and one local minimum, and the curve will go off to negative infinity in one direction. and positive infinity in another. Here are three eampies: The polynomial has some number of real rocts: the points at which the curve crosses the xav. A nibic curve will have either 3 real roots (as above at left, 1 root (above, middle), or in rare cases 2 roots (as above at right). Note that roots are typically single roots, and for single roots, the yurve is negative on one side of the root, positive on the other fa double root results in a tangent to sf fy curve, lhe that above at right). Let a and b be bounds of a root, ie. there is exactly one single root of the polynombl betwenen e and b; To find one root of the polynomial, we can use the following procedure, known as bisection method. it is a form of what is more generally known as binary searche - Because the root is a single root, either flol or f(b) will be positive, and the ocher will be negative, Le. f(a)f(b)