..................................................Mandatory this code in Solar2D and lua............................

Question - Week#8: App should print relative error for varying numbers of trapezoids between 1 and 10,000 (increasing by powers of 10) for the curves from week#8.

I need these things,

Step 1: Write code

Step 2: Record time, LOC, code in PSP log

Step 3: Gather evidence (screenshots, code files etc.)

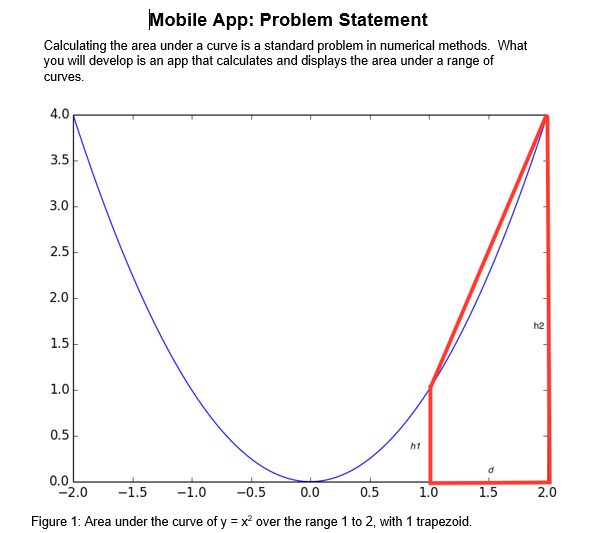
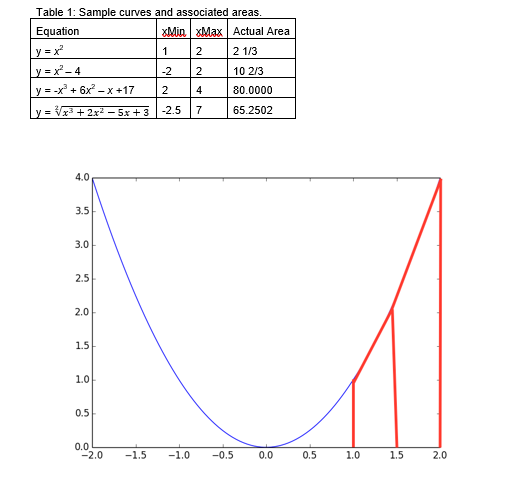
Metrics/Measurement: Software Engineering is about managing process. By managing process, we obtain a product that has consistent quality attributes. Quality thus transfers to the next project. Therefore, software engineers spend time and effort measuring and recording details about the production of software, especially trying to predict future behaviour from past data. Many predictive models for software estimation are of the general form: Person-Months = a* KLOCCb where "a" and "b" are defined constants, "*n and " n are the usual multiplication/exponentiation operators and KLOC means thousands of lines of code (In your model, you would replace person-months with person- hours or minutes and KLOC with LOC as your programs are small). When using this type of model, two questions arise. First, where do these constants come from and second, could this model be used as-is or would it need to be calibrated for each organisation or application domain? The constants come from fitting a curve (the above equation) to known data about projects (their KLOC and PM results). Calibration is essential as every software development firm is different and capabilities differ across project teams. A common method used to fit curves to data is least-squares regression. For a linear model, the equation is often expressed as: y=mx+b, where " m " is the slope of the line and " b " is the point where the line crosses the y-axis (called the y-intercept). Calculate constants for a predictive model, based on your collected data. There should be at I a st eight data points. Use the last seven LOC/time data points for this purpose. Keep the first point aside for validation. The above equation will need to be transformed into a linear form to usethe linear model above. Use: Log Person-hours (or minutes) =loga+b Log LOC (in this case "Log a" represents the "b" parameter in y=mx+b. There are several tools/packages/languages you could use to perform this task (e.g., Excel, R, SPSS, Python). Having created a model that predicts time from LOC, use the actual values for LOC from the first Lua module/function written to predict the time to complete the first Lua task. Is the estimate similar to the actual time taken? Discuss the difference or similarity. Note: As the purpose of this component is to measure aspects of your PSP, the marks for this component of the assessment are given based solely on your supplied PSP data. Mobile App: Problem Statement Calculating the area under a curve is a standard problem in numerical methods. What you will develop is an app that calculates and displays the area under a range of curves. igure 1 : Area under the curve of y=x2 over the range 1 to , with 1 trapezold. The area can be calculated by drawing one or more polygons (trapezoids) that approximate the curve. We start by drawing a trapezoid that encompasses our curve between the given limits and the x-axis, so for equation 1 of table 1 , it looks like figure 1 . We then calculate the area of the trapezoid. Notice that the trapezoid over-estimates the true area. With enough (smaller) trapezoids we can get a very good approximation to the area under the curve (see figure 2). The sum of the area of the smaller trapezoids is the area under the curve. The area of a trapezoid is given by: A=1/2(h1+h2)d Plot graphs of the equations in table 1 for varying (input) total numbers of trapezoids. Compute and display the area between each curve and the x-axis. The number of trapezoids should be a positive integer. Extend your app by allowing the input of varying min and max x limits beyond those in Table 1 , with max>=min Table 1: Sample curves and associated areas. Figure 2: Area under the curve of y=x2 over the range 1 to 2 , with 2 trapezoids. The more trapezoids, the better the approximation approaches the actual area. It is useful to know the error in the calculation. The relative error can be computed by: RE= calculated area actual area actual area %RE= calculated area actual area .100% actual area Extend your app further by plotting \%RE in area values (and the theoretical \%RE line) for a range of trapezoids (1-100,000 in powers of 10 on the x-axis, 0.1-100 in powers of 10 on the y-axis) for each curve in Table 1