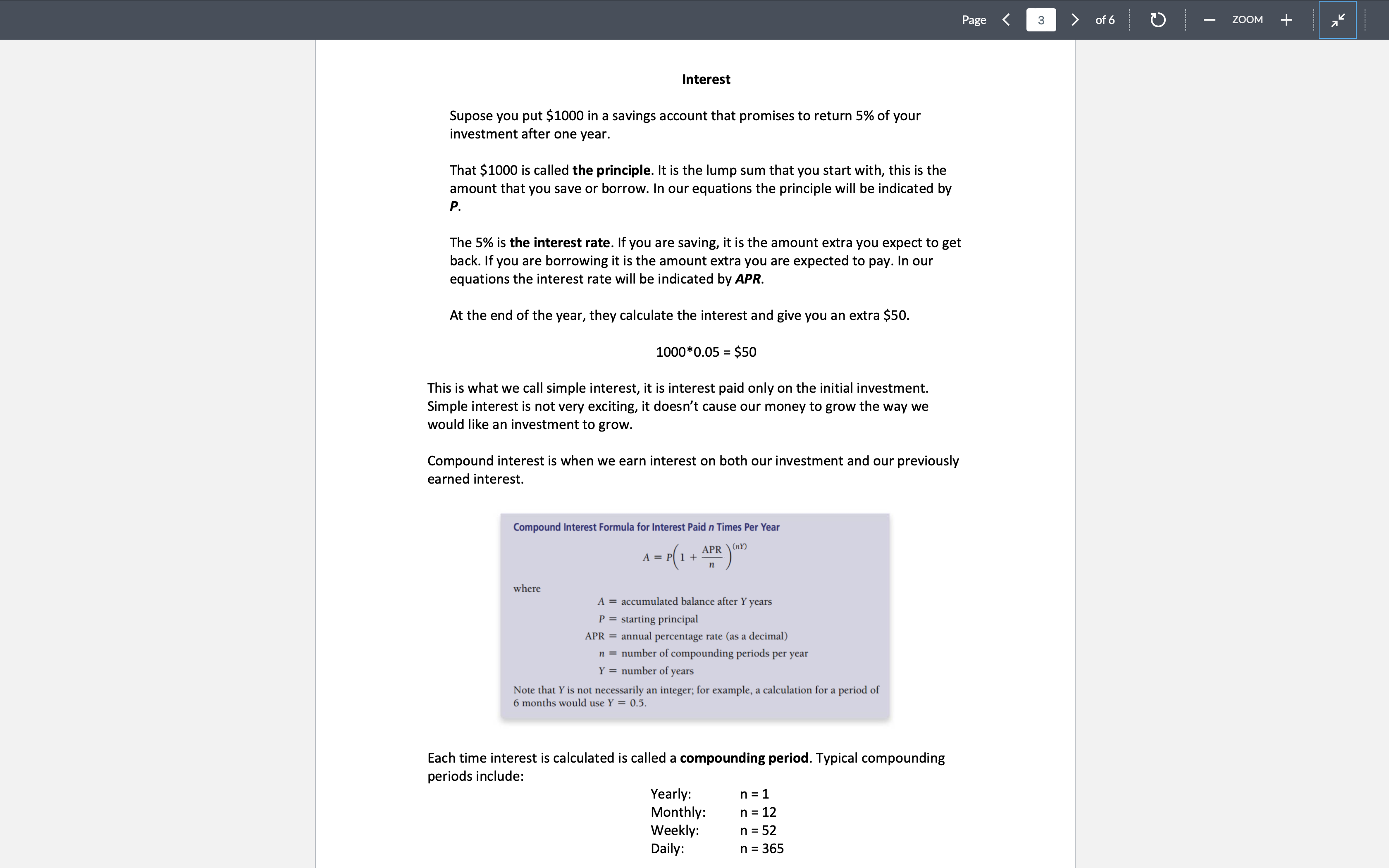
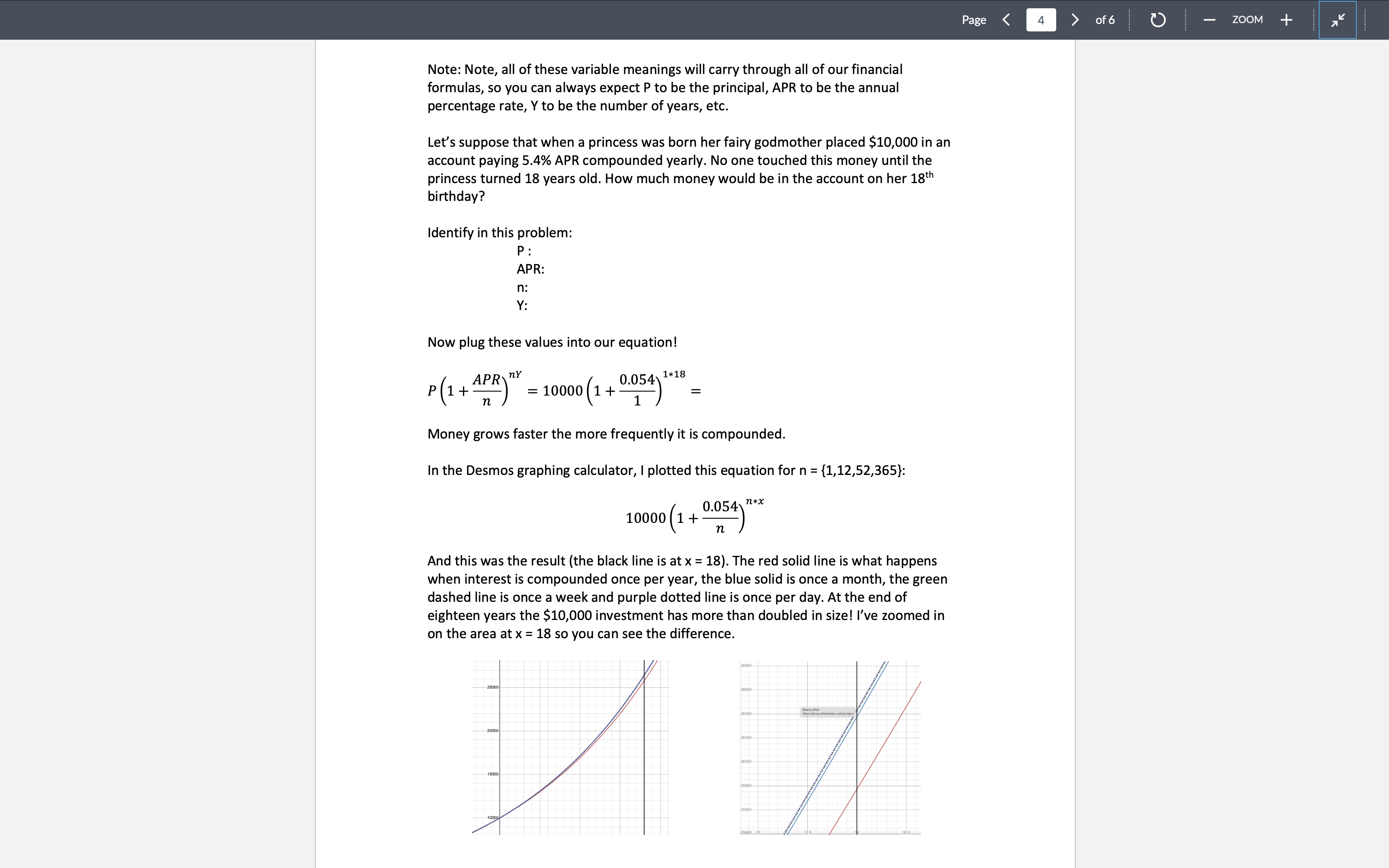
Maria lives with her sister and some friends in a large Arvada apartment. She makes about $750 a week at her job. Her share of the rent is $1000 a month. How much money does she have left over after she pays rent? Assume a month is 4.5 weeks long. Maria spends around $150 a week on groceries. How much money does she have left over after paying rent and buying food? Maria likes to go to the movies twice a month as a treat. She's been going on Friday nights when tickets cost $13.50. How much does that cost her a year? The movie theater wants to encourage more people to buy tickets in the afternoon on Sundays and offers tickets for $8.00 at that time. If Maria switches from Friday nights to Sunday afternoons, how much does she save in a year? Page < 2 of 6 ZOOM Maria switches from seeing movies on Friday nights to Sunday afternoons but decides to keep her budget the same as when she watched movies on Friday nights. How many more movies can she see in a year if she goes to the cheaper show? Budget Problem #2 Your band has been offered a slot to play SXSW! You have 13 months to prepare. You estimate that your band will need to save at least $7500 between now and then. How much money does the band need to set aside each month? The band orders $1500 in special effects for the performance and pay for it by credit card. The annual interest rate is 18.5 %. How much is the interest after the first month (monthly interest is calculated as the loan amount times the annual rate divided by 12)? If you only pay the interest each month and then pay off the balance in full with your SXSW earnings, how much will you end up spending for the effects? Assume that you pay the interest twelve times. + 71 Interest Page < 3 of 6 ZOOM Supose you put $1000 in a savings account that promises to return 5% of your investment after one year. That $1000 is called the principle. It is the lump sum that you start with, this is the amount that you save or borrow. In our equations the principle will be indicated by P. The 5% is the interest rate. If you are saving, it is the amount extra you expect to get back. If you are borrowing it is the amount extra you are expected to pay. In our equations the interest rate will be indicated by APR. At the end of the year, they calculate the interest and give you an extra $50. 1000*0.05 = $50 This is what we call simple interest, it is interest paid only on the initial investment. Simple interest is not very exciting, it doesn't cause our money to grow the way we would like an investment to grow. Compound interest is when we earn interest on both our investment and our previously earned interest. Compound Interest Formula for Interest Paid n Times Per Year where APR \(nY) A = P 1 + n A = accumulated balance after Y years P = starting principal APR = annual percentage rate (as a decimal) n = number of compounding periods per year Y = number of years Note that Y is not necessarily an integer; for example, a calculation for a period of 6 months would use Y = 0.5. Each time interest is calculated is called a compounding period. Typical compounding periods include: Yearly: Monthly: Weekly: Daily: n = 1 n = 12 n = 52 n = 365 + 71 Page < 4 of 6 ZOOM Note: Note, all of these variable meanings will carry through all of our financial formulas, so you can always expect P to be the principal, APR to be the annual percentage rate, Y to be the number of years, etc. Let's suppose that when a princess was born her fairy godmother placed $10,000 in an account paying 5.4% APR compounded yearly. No one touched this money until the princess turned 18 years old. How much money would be in the account on her 18th birthday? Identify in this problem: P: APR: n: Y: Now plug these values into our equation! P1+ (1 APR)" NY = 10000 1+ (1+ 1*18 0.054 1 = Money grows faster the more frequently it is compounded. In the Desmos graphing calculator, I plotted this equation for n = {1,12,52,365}: (1 + 0.054) 10000 1+ n n*x And this was the result (the black line is at x = 18). The red solid line is what happens when interest is compounded once per year, the blue solid is once a month, the green dashed line is once a week and purple dotted line is once per day. At the end of eighteen years the $10,000 investment has more than doubled in size! I've zoomed in on the area at x = 18 so you can see the difference. 25000 20000 26800- 26600 ShareLaTeX 26400- https://www.sharelatex.com/project 26200 15000 10000 26000 25800- 25600- 25400 + 71 This chart shows the value of this investment at different compounding: Compounding Frequency Yearly Monthly Weekly Daily Amount after 18 years $25,771 $26375 $26419 $26430 Page < 5 of 6 ZOOM We can see from the numbers that more frequent compounding is a better investment! You try: You invest $1000 in an account paying 4.8% APR compounded weekly. How much money is in the account at the end of 8 years? Identify in this problem: P: APR: n: Y: Now plug these values into our equation! P(1+ APR) - = If compounding more frequently results in more money, what if we were compounding every moment? We call this continuous compounding and believe it or not, we have an equation for it! Compound Interest Formula for Continuous Compounding where A = PX (APRXY) A = accumulated balance after Y years P = starting principal APR = annual percentage rate (as a decimal) Y = number of years The number e is a special irrational number with a value of e 2.71828. You can compute e to a power with the key on your calculator. Note that this equation uses the number e. This is a special number that appears in a lot of math and science equations (like ) so we gave it a special name (like ). Your calculator has an e function and if you type e into Desmos, it will know what you mean! + 71 Going back to the fairy godmother problem we can see that this equation returns $26432 at the end of 18 years! 10000e (0.054*18) = 26432.2562768 $26432 Page < 6 of 6 ZOOM You try: You invest $1000 in an account paying 4.8% APR compounded continuously. How much money is in the account at the end of 8 years? Identify in this problem: P: APR: Y: Now plug these values into our equation! Pe (APR*Y) = File Preview + 71