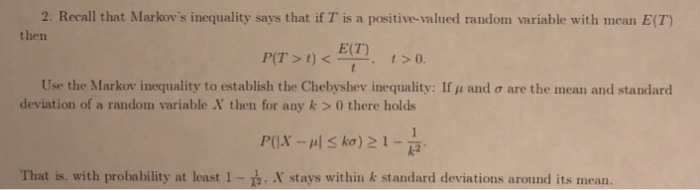Markov inequality

Consider a Markov chain {Xn, n = 0, 1, . ..} on the state space S = {0, 1, 2}. Suppose that the Markov chain has the transition matrix 2 10 10 10 2 P = 3 10 2 4 10 10 1. Show that the Markov chain has a unique stationary mass. 2. Let h denote the stationary mass of the Markov chain. Find h(x) for all x E S. 3. Show that the Markov chain has the steady state mass. 4. Let h* denote the steady state mass of the Markov chain. Find h*(x) for all x E S.4. Consider the Markov chain X" = {X,} with state space S = {0, 1, 2, ...} and transition probabilities 1 ifj=i-1 Puj = 10 otherwise , for i 2 1 and Poo = 0, Poj = for j > 1. (a) Is this Markov chain irreducible? Determine the period for every state. (b) Is the Markov chain recurrent or transient? Explain. (c) Is the Markov chain positive recurrent? If so, compute the sta- tionary probability distribution. (d) For each state i, what is the expected number of steps to return to state i if the Markov chain X starts at state i? 5. Consider a Markov chain X = {X} with state space S = {0, 1, 2, ...} and transition probability matrix 0 1 0 0 P 0 0 P = O p 0 q 0 0 . . . 0 0 P 0 4 0 Here p > 0, q > 0 and p+q =1. Determine when the chain is positive recurrent and compute its stationary distribution.2. Recall that Markov's inequality says that if T' is a positive-valued random variable with mean E(T) then E(T) P(T > 1 ) 0 there holds P(1X - #| Ska) 21 - 1 That is. with probability at least 1 - 2. X stays within & standard deviations around its mean.2. (10 points)(The Weak Law of Large Numbers) In order to estimate 3", the true fraction of smokers in a large population, Alvin selects u. people at random. His estimator Mn is obtained by dividing S", the number of smokers in his sample, by N, i.e., Mn = \"/11. Alvin chooses the sample size n to be the smallest possible number for which the Chebyshev inequality yields a guarantee that PiIMnfl 2 6) 5: where E and 6 are some prespeeied tolerances. Determine how the value of 11 recommended by the Chebyshev inequality changes in the following cases. (a) (5 points] The value of e is reduced to half its original value. (b) (5 points] The value of 5 is reduced to half its original value