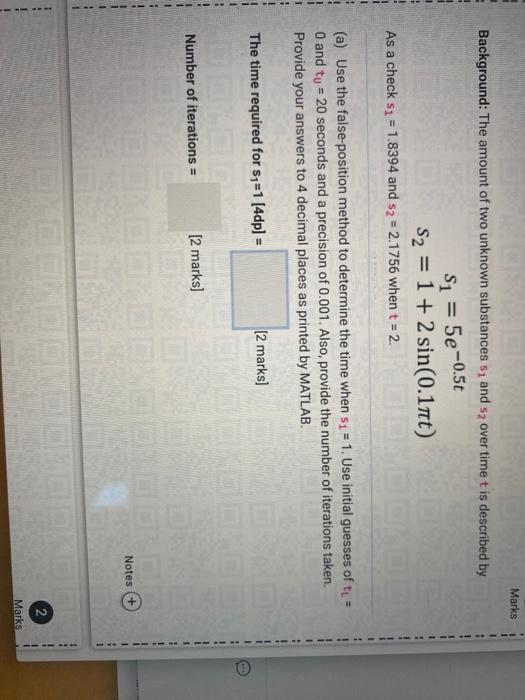
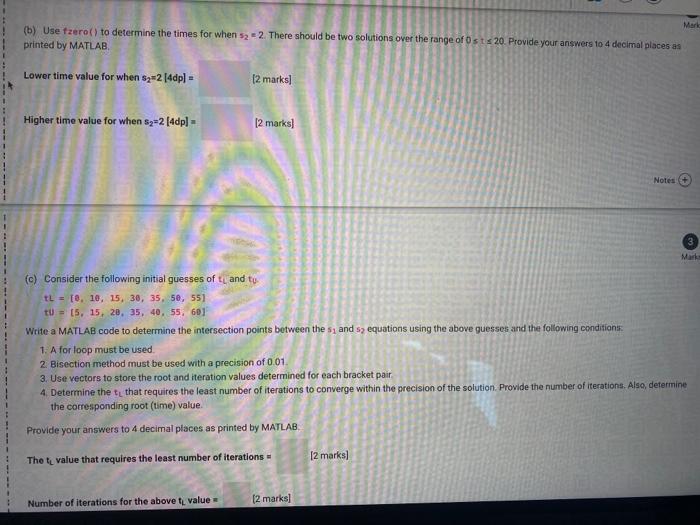
Marks Background: The amount of two unknown substances s and s2 over time t is described by Si = 5e -0.5t S2 = 1 + 2 sin(0.1nt) ) As a check si = 1.8394 and s2 = 2.1756 when t = 2. 1 (a) Use the false-position method to determine the time when s1 = 1. Use initial guesses of tu = O and ty = 20 seconds and a precision of 0.001. Also provide the number of iterations taken Provide your answers to 4 decimal places as printed by MATLAB. 1 The time required for sy=1 [4dp) = [2 marks] Number of iterations = [2 marks] Notes + 2 Marks Mark (b) Use tzero() to determine the times for when 52 = 2. There should be two solutions over the range of Ost $20. Provide your answers to 4 decimal places as printed by MATLAB Lower time value for when sz=2 [4dp] = [2 marks] Higher time value for when sz=240p] = [2 marks] Notes + Marle (c) Consider the following initial guesses of t and tu t1 = te, 10, 15, 30, 35, 50, 551 tu = [5, 15, 20, 35, 40, 55, 601 Write a MATLAB code to determine the intersection points between the 51 and sy equations using the above guesses and the following condition 1. A for loop must be used 2. Bisection method must be used with a precision of 0.01 3. Use vectors to store the root and iteration values determined for each bracket pair 4 Determine the t that requires the least number of iterations to converge within the precision of the solution Provide the number of iterations. Also, determine the corresponding root (time) value Provide your answers to 4 decimal places as printed by MATLAB Thot, value that requires the least number of iterations - [2 marks] Number of iterations for the above t value (2 marks] Number of iterations for the above t value = [2 marks] Corresponding root (time) value [4dp] [2 marks] Copy and paste your MATLAB code into the textbox of the next question. Notes 3 Mu Copy and paste your MATLAB code for part (c) in the previous question in the plain text box below. You can also upload your m-file below (optional). [6 marks] BIU. Maximum size for new files: 2GB, maximum attachments 1 Marks Background: The amount of two unknown substances s and s2 over time t is described by Si = 5e -0.5t S2 = 1 + 2 sin(0.1nt) ) As a check si = 1.8394 and s2 = 2.1756 when t = 2. 1 (a) Use the false-position method to determine the time when s1 = 1. Use initial guesses of tu = O and ty = 20 seconds and a precision of 0.001. Also provide the number of iterations taken Provide your answers to 4 decimal places as printed by MATLAB. 1 The time required for sy=1 [4dp) = [2 marks] Number of iterations = [2 marks] Notes + 2 Marks Mark (b) Use tzero() to determine the times for when 52 = 2. There should be two solutions over the range of Ost $20. Provide your answers to 4 decimal places as printed by MATLAB Lower time value for when sz=2 [4dp] = [2 marks] Higher time value for when sz=240p] = [2 marks] Notes + Marle (c) Consider the following initial guesses of t and tu t1 = te, 10, 15, 30, 35, 50, 551 tu = [5, 15, 20, 35, 40, 55, 601 Write a MATLAB code to determine the intersection points between the 51 and sy equations using the above guesses and the following condition 1. A for loop must be used 2. Bisection method must be used with a precision of 0.01 3. Use vectors to store the root and iteration values determined for each bracket pair 4 Determine the t that requires the least number of iterations to converge within the precision of the solution Provide the number of iterations. Also, determine the corresponding root (time) value Provide your answers to 4 decimal places as printed by MATLAB Thot, value that requires the least number of iterations - [2 marks] Number of iterations for the above t value (2 marks] Number of iterations for the above t value = [2 marks] Corresponding root (time) value [4dp] [2 marks] Copy and paste your MATLAB code into the textbox of the next question. Notes 3 Mu Copy and paste your MATLAB code for part (c) in the previous question in the plain text box below. You can also upload your m-file below (optional). [6 marks] BIU. Maximum size for new files: 2GB, maximum attachments 1