Mastery Problem: CVP Analysis - Constructing a Cost-Volume-Profit Chart

CVP Analysis and the Contribution Margin Income Statement

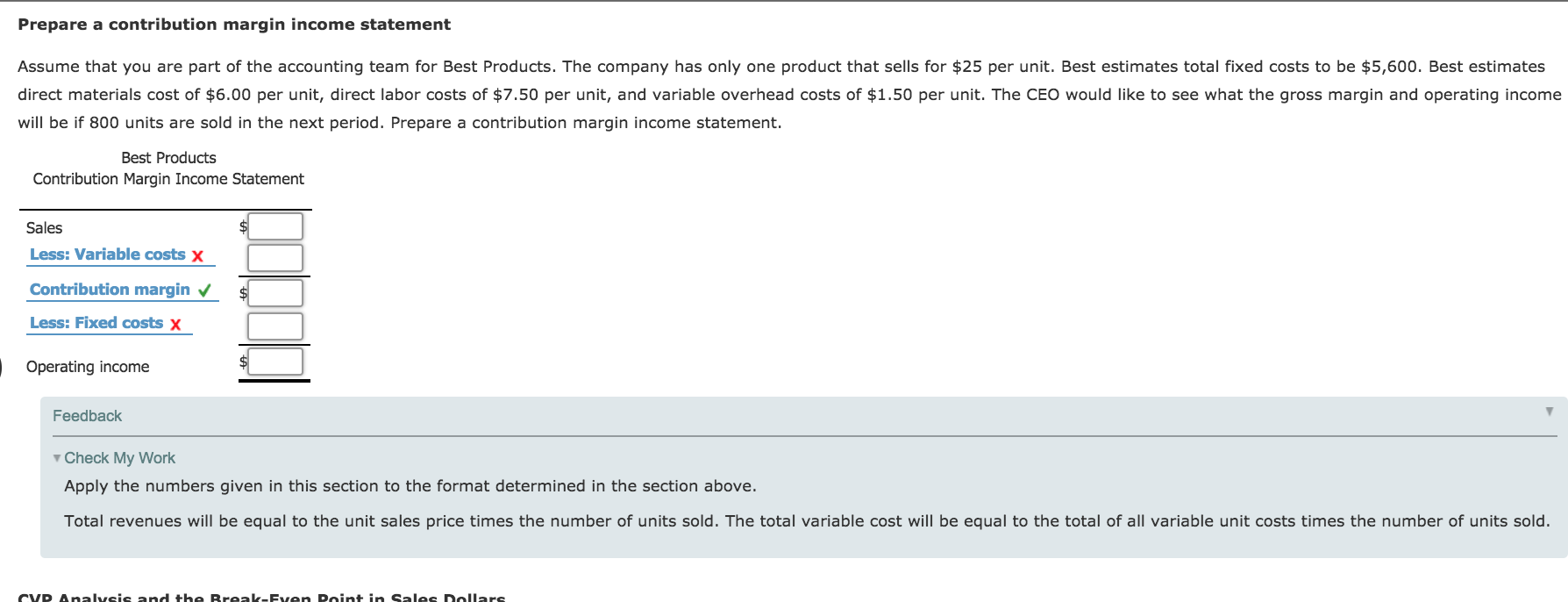
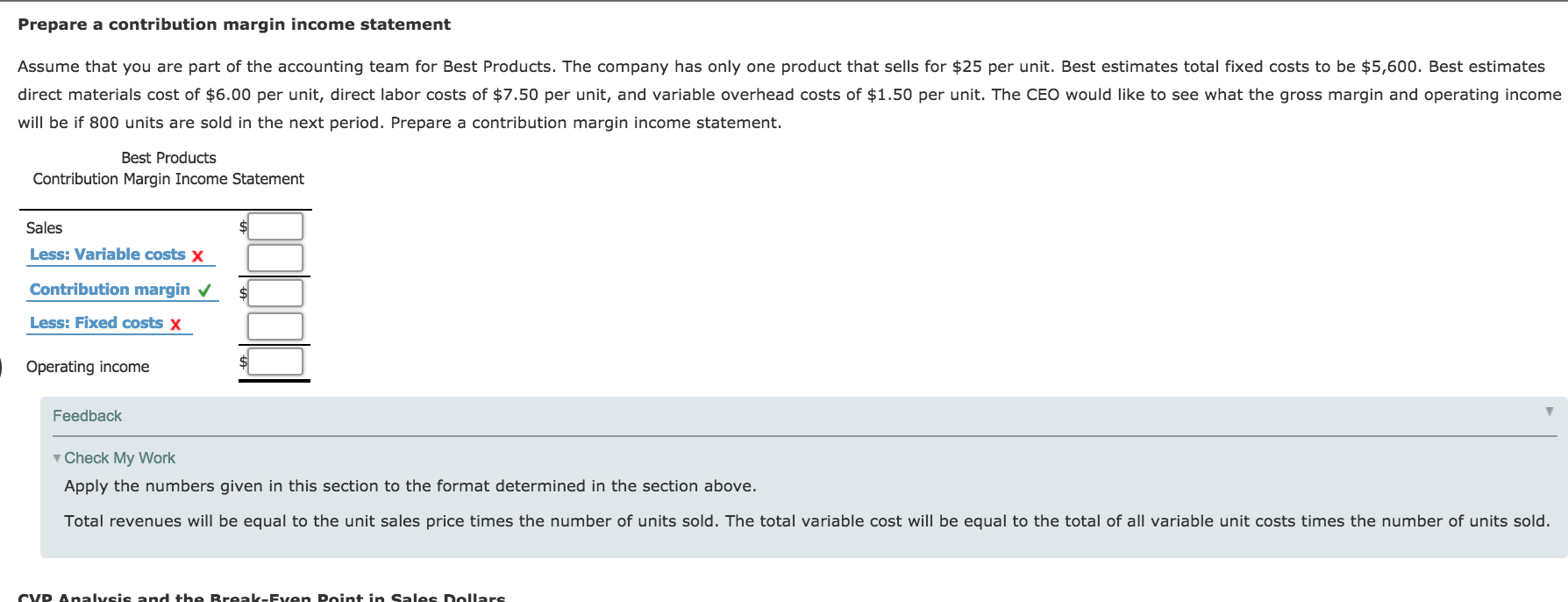
For planning and control purposes, managers have a powerful tool known as cost-volume-profit (CVP) analysis. CVP analysis shows how revenues, expenses, and profits behave as volume changes, which helps identify problems and create solutions. In CVP analysis,costsare classified according to behavior:variableorfixed,rather than by category: product (which includes both variable and fixed) or period (which includes both variable and fixed). When variable costs are subtracted from sales, the contribution margin is obtained, representing the amount of dollars available to cover fixed costs after the costs related to sales are recovered. Fixed costs are deducted from the contribution margin to arrive atoperating income. This format is known as the contribution margin income statement. Complete the following table to illustrate the format.

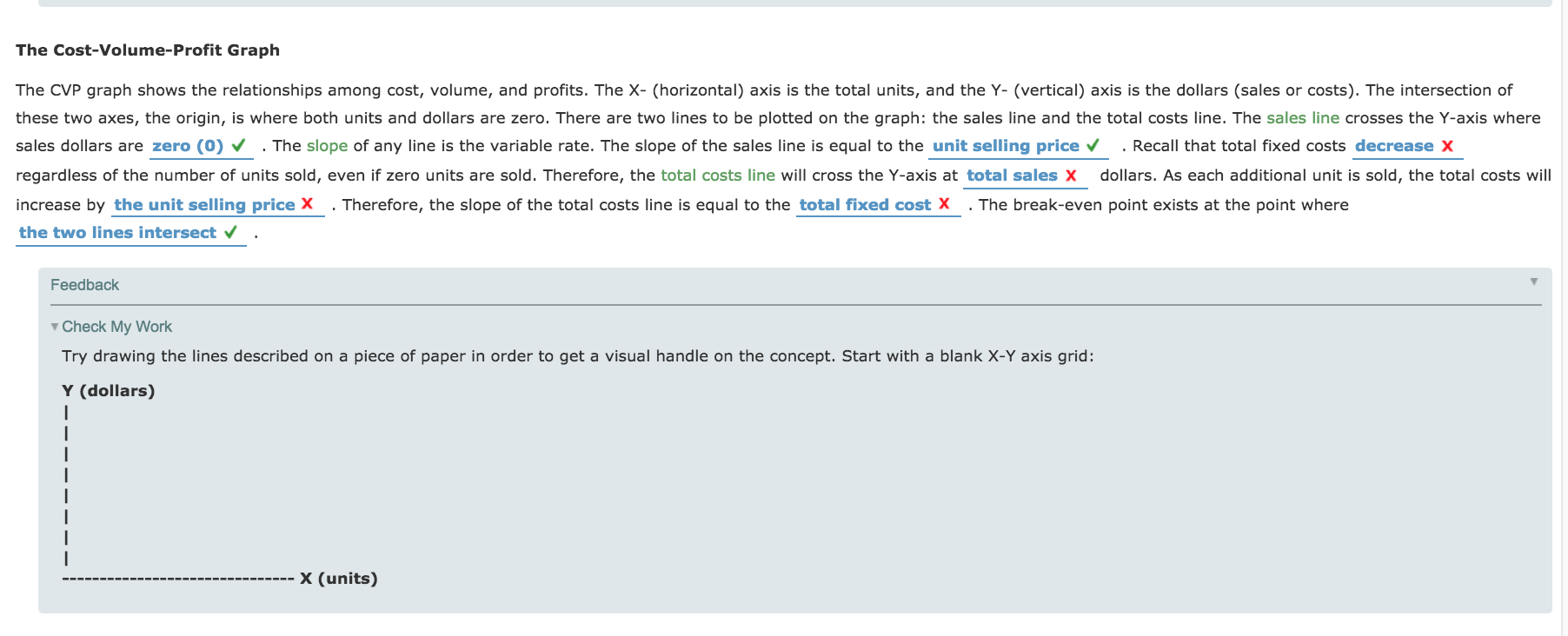
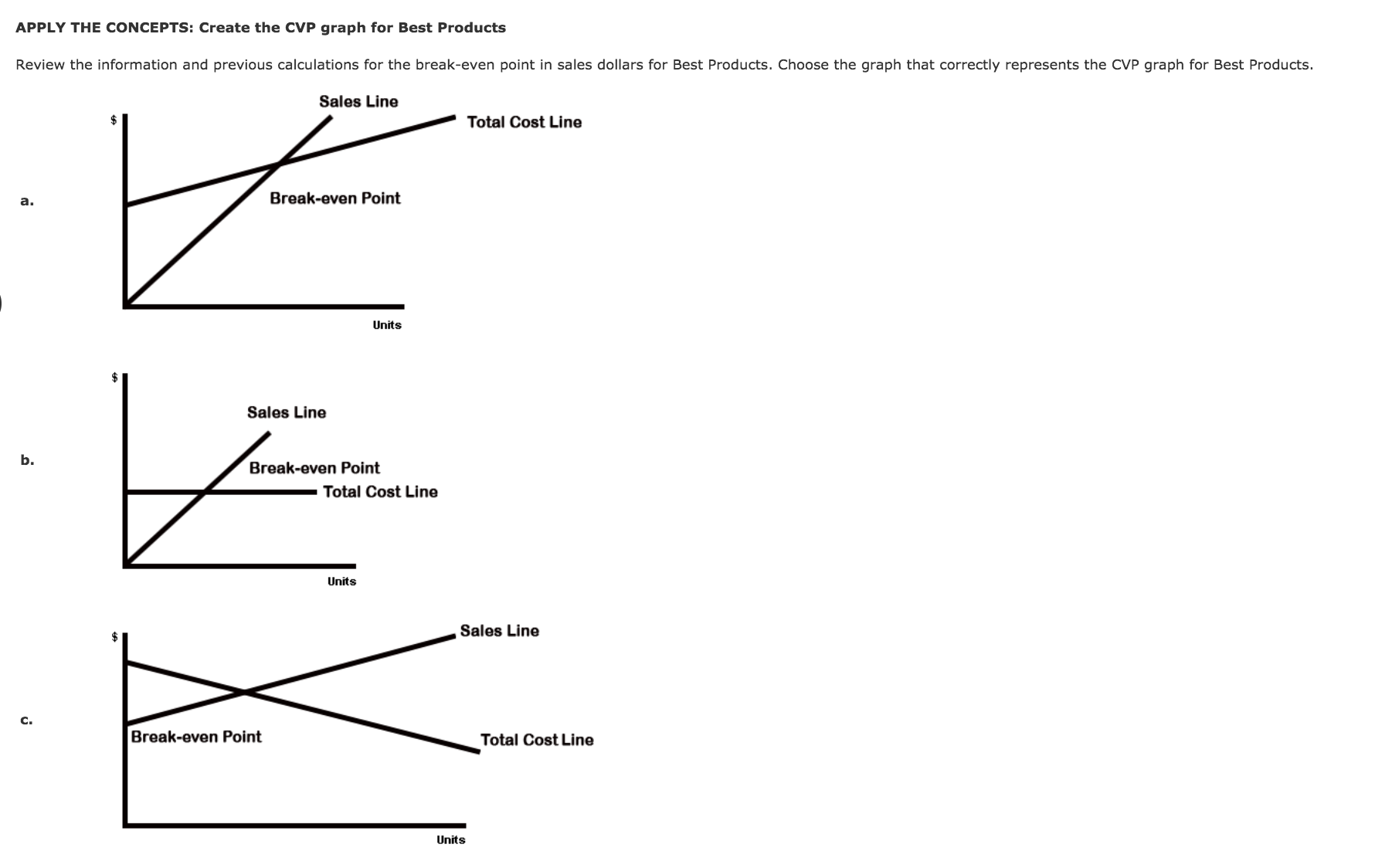
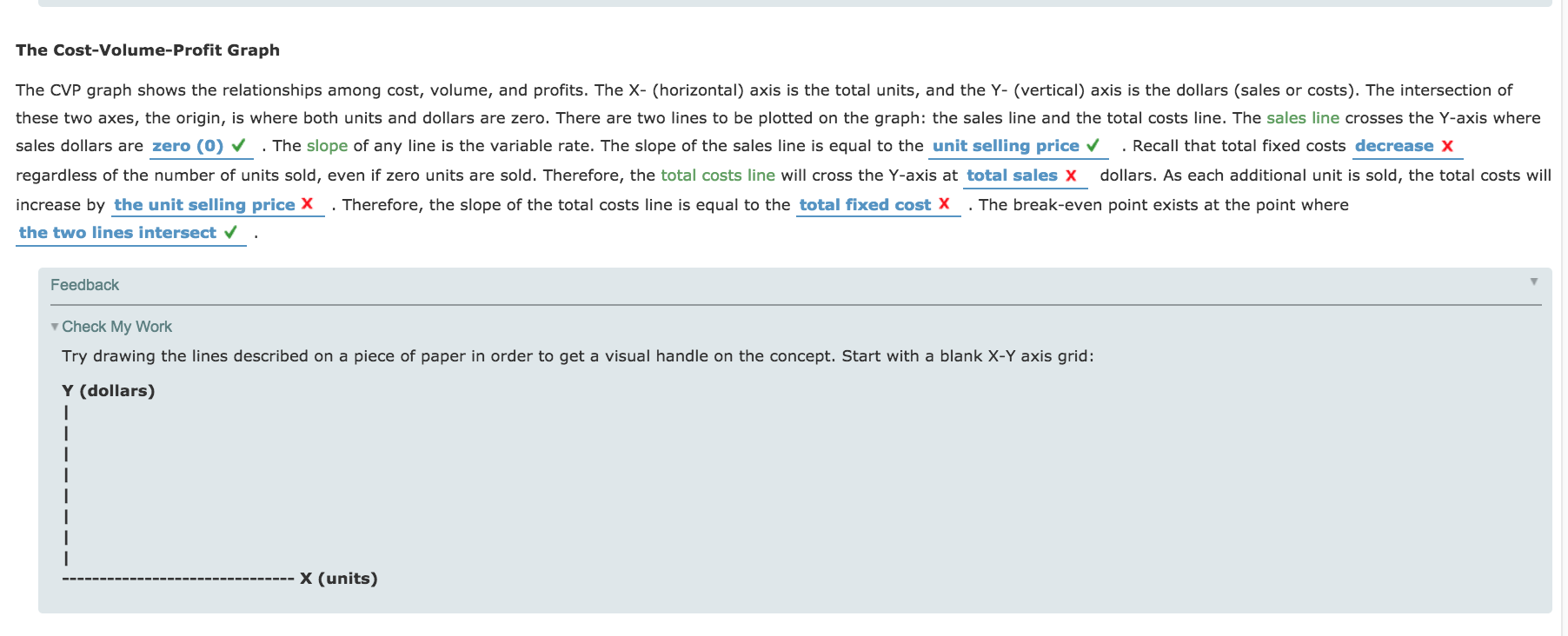
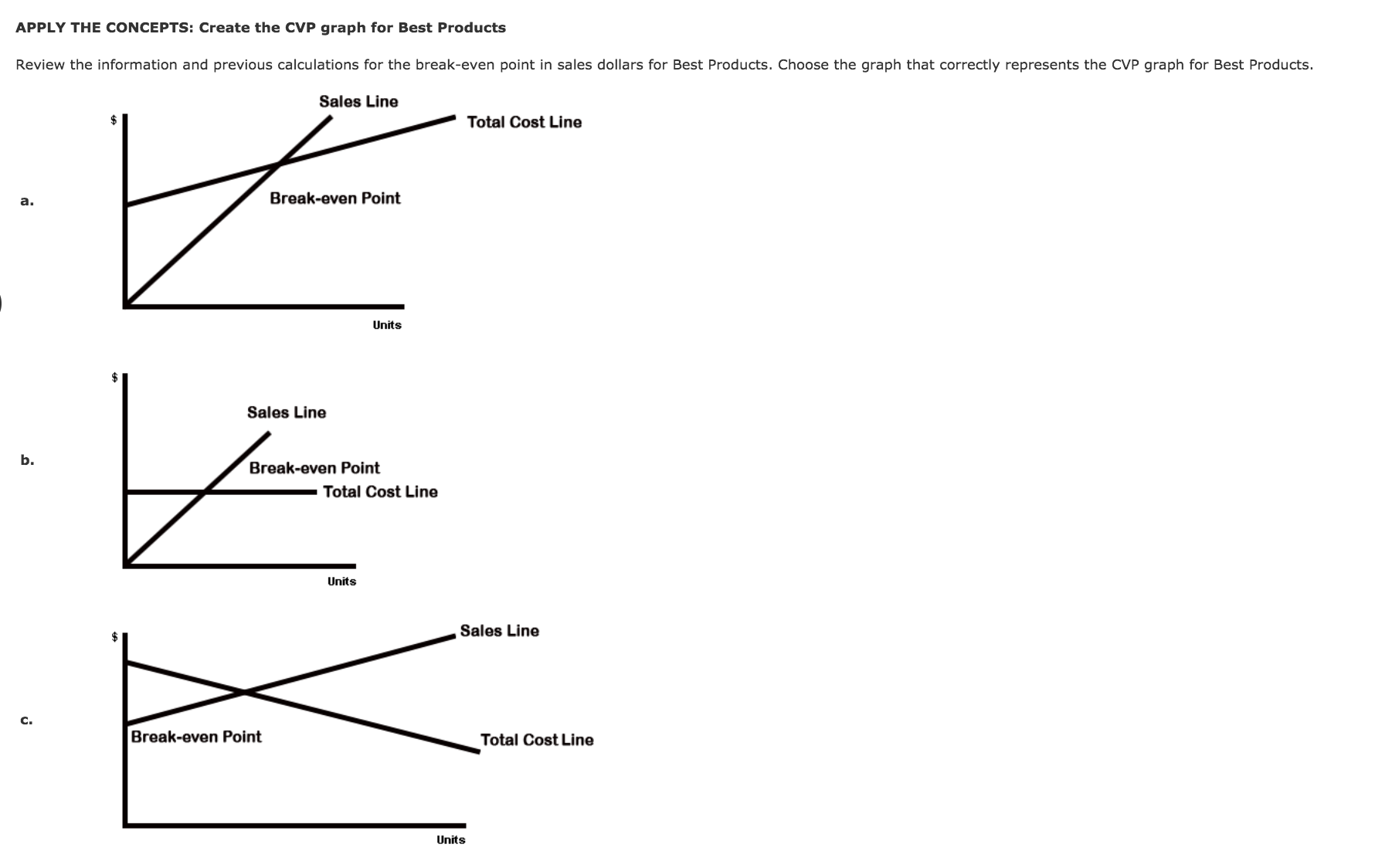
Prepare a contribution margin income statement Assume that you are part of the accounting team for Best Products. The company has only one product that sells for $25 per unit. Best estimates total fixed costs to be $5,600. Best estimates direct materials cost of $6.00 per unit, direct labor costs of $7.50 per unit, and variable overhead costs of $1.50 per unit. The CEO would like to see what the gross margin and operating income will be if 800 units are sold in the next period. Prepare a contribution margin income statement. Best Products Contribution Margin Income Statement Sala $4 L55: Variable cosh x Contribution margin 4 L55: Fixed costs x | Operating inoome # Feed back ' v Check My Work Apply the numbers given in this section to the format determined in the section above. Total revenues will be equal to the unit sales price times the number of units sold. The total variable cost will be equal to the total of all variable unit costs times the number of units sold. rvn Analuai: and u: \"mallluau Ian-lint- 'm Gala: nnllar: APPLY THE CONCEPTS: Calculate the break-even point in sales dollars for Best Products Further analysis of Best Products's fixed costs revealed that the company actually faces annual xed overhead cuss of $5,600 and annual fixed selling and administrative costs of $2,400. Variable cost estimates are correct: direct materials cost, $6.00 per unit; direct labor costs, $7.50 per unit; and variable overhead costs, $1.50 per unit. At this time, the selling price of $25 will not change. Complete the following formulas for the revised xed costs. Enter the ratio as a percentage. Contribution Margin per Unit = $ - $ = 3; Contribution Margin Ratio = $:] = C] % $:l Now complete the formulas for (1) the break-even point in sales dollars and (2) the units sold at the break-even point. To calculate this, divide the break-even point in sales dollars by the unit selling price. Break-Even Point in Sales Dollars = $:] = $:] :1 % Units Sold at Break-Even Point = C] units Assume that the number of units that Best sold exceeded the break-even point by one (1). How much would operating income be? $ What would operating income be if the units sold exceeded the breakeven point by ve (5) units? $ The Cost-Volume-Pro'l'lt Graph The CVP graph shows the relationships among oost, volume, and prots. The X- (horizontal) axis is the total units, and the Y- (vertical) axis is the dollars (sales or costs). The intersection of these two axes, the origin, is where both units and dollars are zero. There are two lines to be plotted on the graph: the sales line and the total costs line. The sales line crosses the Y-axis where sales dollars are zero (0) J , The slope of any line is the variable rate. The slope of the sales line is equal to the unlt oelllng prloe I . Recall that total xed costs decrease X regardless of the number of units sold, even if zero units are sold. Therefore, the total costs line will cross the Y-axis at total lalel 3: dollars. As each additional unit is sold, the total oosts will increase by the unit lelllng prlee X . Therefore, the slope of the total costs line is equal to the total xed out X . The break-even point exists at the point where the two llneo Intersect J . APPLY THE CONCEPTS: Create the CVP graph for Best Products Review the information and previous calculations for the break-even point in sales dollars for Best Products. Choose the graph that correctly represents the CVP graph for Best Products. Sales Line 3 Total Cost Line a. Break-own Point "nib 5 Sales Lino Break-won Point Total GoutLim APPLY THE CONCEPTS: Use the (NP graph to analyze the effecu of changes in price and costs Graph the following on your own paper. At the original position, the break-even point in sales dollars is $24,000 at 500 units. The xed costs are $8,000. Assume the slope of the sales line is equal to the selling price. When the two points of the sales line are at the origin and the break-even point, you see that the slope of the line is $48, which means that the selling price is E . when the two points of the total costs line are at the origin and the break-even point, you see that the slope of the line is $32.00, which means that the variable cost per unit is $:] . Leave the breakeven point (x) at its original position. Use it as a reference point to answer the following questions. Analyze the scenarios by sliding the points on the lines to get the slope desired. Recall that the new break-even point for each scenario exists where the sales and total costs lines intersect. Compare it to the original break-even point (x). (You may want to put the lines back to their original position for each scenario.) Each scenario should be considered independently. 1. The company purchases a fixed asset and increases xed costs by $2,000. Variable costs remain the same, which means that the slope does not change. This will cause the break-even point to move to the left X , which means that break-even point in sales dollars decreases X . 2. A new supplier can provide a product of equal quality at $4.00 per unit less than the current direct materials cost. If the new supplier is used, the slope of the total costs line will be $ , and the break-even point in sales dollars decreases V . 3. Market research shows that a price increase will decrease the number of units sold. A price increase will cause the slope of the sales line to decrease X . But internal analysis shows that this price increase will cause the break-even point in sales to shift to the left 4 , which means that fewer V/ units will need to be sold to break even