mat lab help

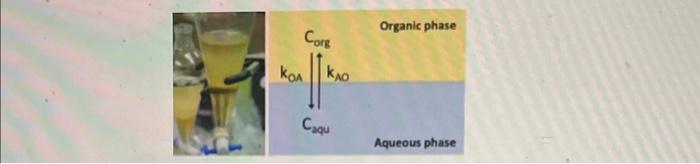
Compute the concentrations of the solute in the two phases after the first 20 time steps using both matrix multiplication and eigenvalue/vector form and generate a plot to compare. Write code that answers the following questions based on your finite difference model and ode45: What fraction of the solute will remain in each phase as time approaches infinity And the extraction is complete when the concentrations in the two phases reaches 99% of the equilibrium value. At what time is the extraction complete? Generate a plot comparing the concentrations of the solute in the two phases over time based based on eigenvalue/vector form and ode45. Represent the ode45 solution as a solid line, while the linear difference solution should be represented as points on the koA=0.1,kAo=0.9,dt=1 and using initial conditions corg, 0=0, and caqu, 0=10 derive the linear difference equations in matrix form for the concentration profiles of the solute in both phases and then transfer them into eigenvaule/vector form We can model the partitioning of the solute between the two phases based on a simple chemical equilibrium using the following differential equations: dtdCm=k01Cas+kn0CapdtdCst=kanCaxk40Ckp In these equations, Ci and Csp are the concentrations of the solute in the organic and aqueous phases. respectively, while kon is the rate of transferring from the organic phase to the aquecus phase and kno is the reverse. Here we will use the following finite diference approximation to find an approximate solution to the system of ODEs: Organic phase Aqueous phase We can model the partitioning of the solute between the two phases based on a simple chemical equilibrium using the following differential equations: dtdCorg=kOACorg+kAOCaqudtdCCaqu=kOACorgkAOCaqu In these equations, Corg and Caqu are the concentrations of the solute in the organic and aqueous phases, respectively, while kOA is the rate of transferring from the organic phase to the aqueous phase and kAO is the reverse. Here we will use the following finite difference approximation to find an approximate solution to the system of ODEs: 1 y(t)tyn+1yn Compute the concentrations of the solute in the two phases after the first 20 time steps using both matrix multiplication and eigenvalue/vector form and generate a plot to compare. Write code that answers the following questions based on your finite difference model and ode45: What fraction of the solute will remain in each phase as time approaches infinity And the extraction is complete when the concentrations in the two phases reaches 99% of the equilibrium value. At what time is the extraction complete? Generate a plot comparing the concentrations of the solute in the two phases over time based based on eigenvalue/vector form and ode45. Represent the ode45 solution as a solid line, while the linear difference solution should be represented as points on the koA=0.1,kAo=0.9,dt=1 and using initial conditions corg, 0=0, and caqu, 0=10 derive the linear difference equations in matrix form for the concentration profiles of the solute in both phases and then transfer them into eigenvaule/vector form We can model the partitioning of the solute between the two phases based on a simple chemical equilibrium using the following differential equations: dtdCm=k01Cas+kn0CapdtdCst=kanCaxk40Ckp In these equations, Ci and Csp are the concentrations of the solute in the organic and aqueous phases. respectively, while kon is the rate of transferring from the organic phase to the aquecus phase and kno is the reverse. Here we will use the following finite diference approximation to find an approximate solution to the system of ODEs: Organic phase Aqueous phase We can model the partitioning of the solute between the two phases based on a simple chemical equilibrium using the following differential equations: dtdCorg=kOACorg+kAOCaqudtdCCaqu=kOACorgkAOCaqu In these equations, Corg and Caqu are the concentrations of the solute in the organic and aqueous phases, respectively, while kOA is the rate of transferring from the organic phase to the aqueous phase and kAO is the reverse. Here we will use the following finite difference approximation to find an approximate solution to the system of ODEs: 1 y(t)tyn+1yn