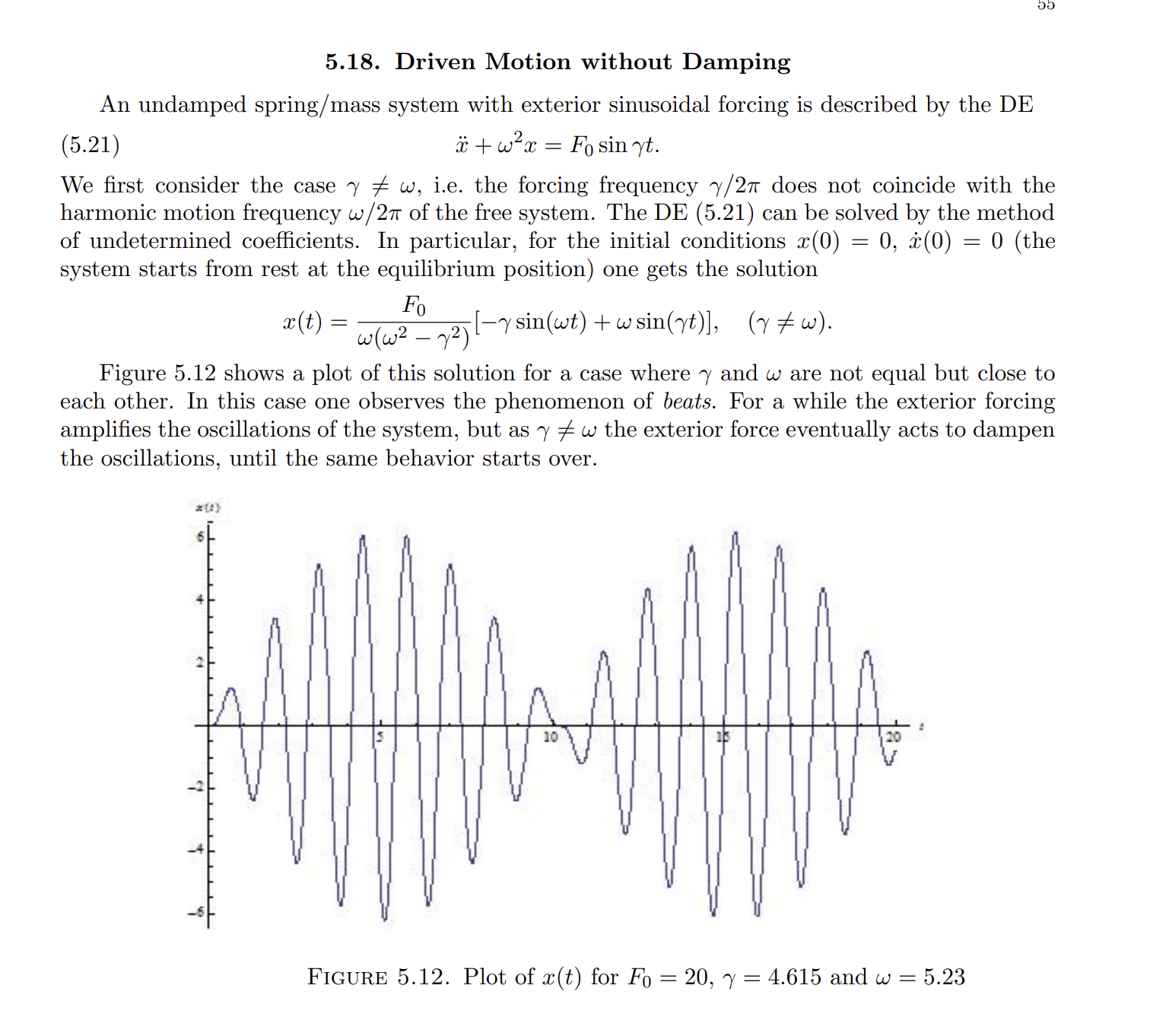
Problem 3: Assume that the length of the concrete sections is L = 19 meters long, that the mass of the car is 1250 kg and the mass of the driver 80 kg. (a) Find Verit for this car and driver. (b) At what velocity does a series of speed bumps at 4 meter spacings get the car into resonance, still assuming broken hydraulic units and the same masses and spring constant as above? Comment on what is achieved by putting speed bumps in a residential neighborhood. (c) Plot the solution curve for x(t) where L, m, k and v = Verit are as in part (a). Use a 2 cm, i.e. the street level varies by 4 cm within 19 meters. (d) Assume that the bottom of the car is 10 inches above the ground when the car is at rest. If you drive at resonance speed, how long does it take for the bottom of the car to hit the road? Problem 4: Suppose you drive at a speed v which is 5% lower than the resonance speed from Problem 3(a). Plot the solution of the initial value problem (0) 0, (0) = 0 for the DE found in Problem 1 for this v. Comment! How would this ride end? = (5.5) 5.4. Solution of the DE for Free Undamped Motion From Section 3.17 we know that the general solution of (5.4) is given by x(t) = C coswt + C2 sin wt. This describes oscillations of time period T = 2T 2/w and frequency f = 1/T = 2 (i.e. the number of oscillations per unit time interval, typically per second or Hz Hertz). 44 5.5. Example 1 on Free Undamped Motion A 20-kg mass stretches a spring by 40 cm. The mass is released from rest to a point 20 cm below the equilibrium position. Using mks-units, find the equation of motion. Solution: We have m = 20 kg and s = 0.4 m. Thus, by Hooke's law, mg k S 20.9.8 0.4 = 490. (Note that we don't have to include units as long as we consistently use the proper units from the mks-system in our calculations.) We also have w = k/m = = 490/20 = 7/2. From the equation of free harmonic motion we find wx = x + x= = 0. Its general solution is (5.6) 49 x(t) = = c1 cos(wt) + C2 sin(wt). = The constants C1 and C2 are found from the initial conditions x(0) +0.2 (recall that we choose the x-axis to be pointing downwards) and x(0) = 0 (this is what it means to start from rest). Inserting t = 0, x = 0.2 into (5.6) gives 0.2 = c2. To make use of the other initial condition, we have to take the derivative of (5.6), (t) = c1w sin(wt) + cw cos(wt). Inserting t = 0, x = 0 gives 0: = cw or C2 = = 0. Thus the equation of motion is x(t) = 0.2 cos 7 () t meters. 55 5.18. Driven Motion without Damping An undamped spring/mass system with exterior sinusoidal forcing is described by the DE (5.21) +wx = Fo sin yt. We first consider the case y + w, i.e. the forcing frequency Y/2T does not coincide with the harmonic motion frequency w/2 of the free system. The DE (5.21) can be solved by the method of undetermined coefficients. In particular, for the initial conditions x(0) system starts from rest at the equilibrium position) one gets the solution x(t) Fo w(w - y) -y sin(wt) + w sin(yt)], (vw). = 0,(0) = 0 (the Figure 5.12 shows a plot of this solution for a case where y and w are not equal but close to each other. In this case one observes the phenomenon of beats. For a while the exterior forcing amplifies the oscillations of the system, but as y + w the exterior force eventually acts to dampen the oscillations, until the same behavior starts over. 2 FIGURE 5.12. Plot of x(t) for Fo = 20, y = 4.615 and w = 5.23 5.19. Pure Resonance Solving the DE (5.21) with initial values x(0) = 0, x(0) = solution Fo Fo x(t) = sin(wt). - -t cos(wt). 2w2 2w 0 for the case y = w yields the The frequency Y/2 of the driving force is equal to the frequency w/2 of free oscillations. As a result the oscillations become larger and larger in time, see Figure 5.13. A real system in this state of pure resonance would necessarily fail once the spring is stretched beyond its elastic limit. Including an additional damping term of the form 2x in (5.21) would prevent the resonance from happening.