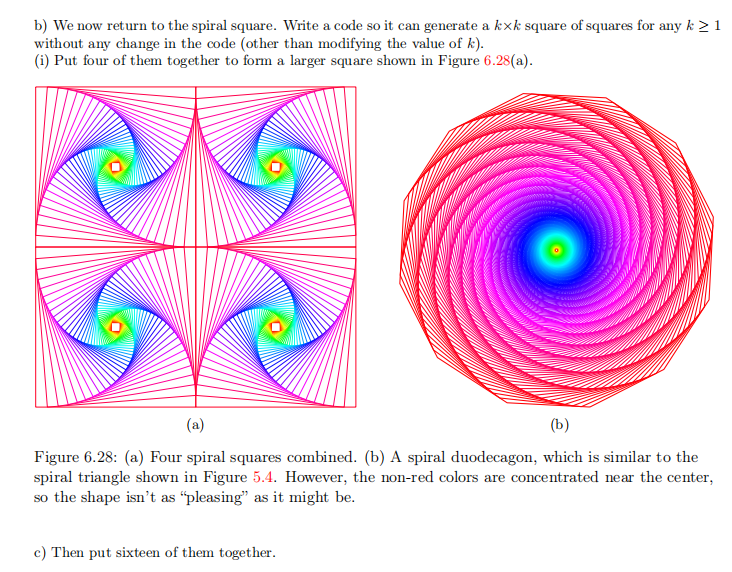
matlab

35) In Problem 5.9-7 you are to generalize the spiral triangle script file spiral_triangle to a regular polygon with m sides for any m > 3 by modifying the script file "slightly". a) Convert this script file to the function fspiralgon whose input arguments are m, n, d_angle, rotate, and shift, so take out statements (1,2). The fourth input argument rotates the initial polygon, i.e., the inner one, by an additional rotate degrees, and the fifth argument shift shifts the center of all these polygons to the point (shift(1), shift(2)). (i) Plot a spiral square for n = 41 and d angle = 2.25, then for n = 21 and d_angle = 4.5, and finally for for n = 11 and d_angle = 9. However, it should look like a square and not a diamond, i.e., the sides should start end end perfectly horizontal and vertical. (ii) Repeat the above images, but the square should rotate 180 by "doubling" n. (iii) Plot a spiral pentagon which rotates a total of 180. Use "pleasing" values of n and d_angle. (iv) Plot a spiral octagon which rotates a total of 360. Use "pleasing" values of n and d_angle. b) We now return to the spiral square. Write a code so it can generate a kxk square of squares for any k > 1 without any change in the code (other than modifying the value of k). (i) Put four of them together to form a larger square shown in Figure 6.28(a). (a) (b) Figure 6.28: (a) Four spiral squares combined. (b) A spiral duodecagon, which is similar to the spiral triangle shown in Figure 5.4. However, the non-red colors are concentrated near the center, so the shape isn't as "pleasing" as it might be. c) Then put sixteen of them together. 35) In Problem 5.9-7 you are to generalize the spiral triangle script file spiral_triangle to a regular polygon with m sides for any m > 3 by modifying the script file "slightly". a) Convert this script file to the function fspiralgon whose input arguments are m, n, d_angle, rotate, and shift, so take out statements (1,2). The fourth input argument rotates the initial polygon, i.e., the inner one, by an additional rotate degrees, and the fifth argument shift shifts the center of all these polygons to the point (shift(1), shift(2)). (i) Plot a spiral square for n = 41 and d angle = 2.25, then for n = 21 and d_angle = 4.5, and finally for for n = 11 and d_angle = 9. However, it should look like a square and not a diamond, i.e., the sides should start end end perfectly horizontal and vertical. (ii) Repeat the above images, but the square should rotate 180 by "doubling" n. (iii) Plot a spiral pentagon which rotates a total of 180. Use "pleasing" values of n and d_angle. (iv) Plot a spiral octagon which rotates a total of 360. Use "pleasing" values of n and d_angle. b) We now return to the spiral square. Write a code so it can generate a kxk square of squares for any k > 1 without any change in the code (other than modifying the value of k). (i) Put four of them together to form a larger square shown in Figure 6.28(a). (a) (b) Figure 6.28: (a) Four spiral squares combined. (b) A spiral duodecagon, which is similar to the spiral triangle shown in Figure 5.4. However, the non-red colors are concentrated near the center, so the shape isn't as "pleasing" as it might be. c) Then put sixteen of them together