(matlab code only)(matlab code only)(matlab code only)(matlab code only)(matlab code only)

Perform the same computation as in Sec. 12.2, but for the truss depicted below.

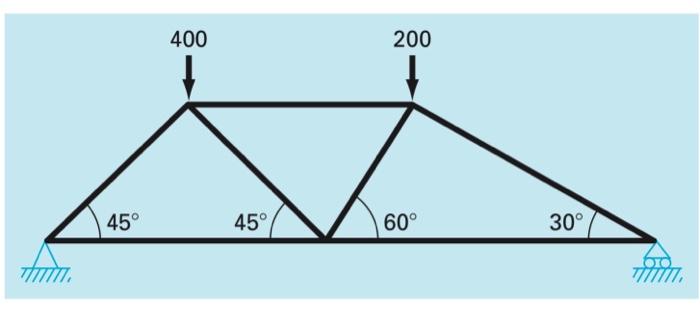
pls write the code for the truss depicted below, the code above is sample code from another truss

% Case Study 12.2: Statically determinate truss A = (-cosd (30) O cosd (60) 0 0 0; sind(30) O sind (60) 0 0 0; cosd(30) 10100; sind(30) 0 0 0 1 0; 01 cosd(60) O O 0; 00 sind (60) 0 0 1]; b = [0 -1000 O O O O]'; $ the easy way... 8 X =A\b; & forward elimination step n = 6; & dimension of A for k=1:n-1 % partial pivot (swap row k with the row that has max value) [value, index] = max(abs (A(:n,k))); $max function returns index too swap - k+index-1; % row index to swap with k temp = A(swap, :); $ need a temporary variable to store row A(swap, :) = A(k, :); A(K,:) = temp; $ also swap elements of b temp = b(swap); b(swap) = b(k); b(k) = temp; for i=k+1:n factor = A(1,k)/A(k, k); Ali, :) = Ali,:) - factor*A(k, :); b(i) = b(i) - factor+b(k); end end $check: is A upper triangular now? disp(A); & back substitution x = zeros(n,1); x(n) b(n)/ A(n,n); for i=n-1:-1:1 x(i) = (b(i) - A(i,i+1:n)*x(i+1:n)) / Ali, i); end disp(x); $ the answer! (we hope.) 400 200 45 45 60 30 % Case Study 12.2: Statically determinate truss A = (-cosd (30) O cosd (60) 0 0 0; sind(30) O sind (60) 0 0 0; cosd(30) 10100; sind(30) 0 0 0 1 0; 01 cosd(60) O O 0; 00 sind (60) 0 0 1]; b = [0 -1000 O O O O]'; $ the easy way... 8 X =A\b; & forward elimination step n = 6; & dimension of A for k=1:n-1 % partial pivot (swap row k with the row that has max value) [value, index] = max(abs (A(:n,k))); $max function returns index too swap - k+index-1; % row index to swap with k temp = A(swap, :); $ need a temporary variable to store row A(swap, :) = A(k, :); A(K,:) = temp; $ also swap elements of b temp = b(swap); b(swap) = b(k); b(k) = temp; for i=k+1:n factor = A(1,k)/A(k, k); Ali, :) = Ali,:) - factor*A(k, :); b(i) = b(i) - factor+b(k); end end $check: is A upper triangular now? disp(A); & back substitution x = zeros(n,1); x(n) b(n)/ A(n,n); for i=n-1:-1:1 x(i) = (b(i) - A(i,i+1:n)*x(i+1:n)) / Ali, i); end disp(x); $ the answer! (we hope.) 400 200 45 45 60 30