MATLAB CODING:

The Maclaurin series expansion for the sine function is:

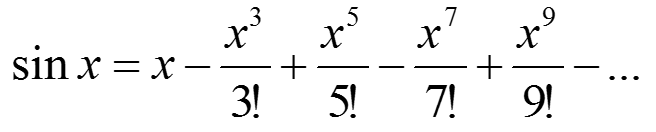
where x is in radians. This function can be used to approximate the sine of x with increasing accuracy as terms are added to the summation. Write a function that accepts two scalar inputs (in order):

1. A value for x (in radians).
2. The number of series sums, N , to use in the series approximation of sin(x).

Your function should generate the following three outputs (in order):

1. A column vector of the first N series summations. Consider the first summation to be x-x^3/3!.
2. A column vector of the magnitude (i.e. absolute value) of the approximate relative error values associated with the first N series summations. Note the "previous approximation" for the first value in this vector will be x.
3. A column vector of the true relative error values associated with the first N series summations. Use MATLAB's built-in sine function to compute the true value for this error calculation.

Note: The first two test cases test the results for the first and second series sums respectively to aid in your debugging process.

Please help edit my code for the required process above, thank you!

CODE:

function [series_sums, approx_rel_error, true_rel_error] = student_solution(x, number_of_sums) true_value = sin(x); series_sums_loop = linspace(0,0,number_of_sums); approx_rel_error_loop = linspace(0,0,number_of_sums); true_rel_error_loop = linspace(0,0,number_of_sums); num_time = 1; for ndx = 1:number_of_sums current_approx = (x^num_time/(factorial(num_time))); prev_approx = (x^(num_time-2)/(factorial(num_time-2))); series_sums_loop(ndx) = current_approx; approx_rel_error_loop(ndx) = (current_approx-prev_approx)/current_approx; true_rel_error_loop(ndx) = (true_value-current_approx)/true_value; num_time = num_time + 2; end series_sums = series_sums_loop approx_rel_error = approx_rel_error_loop true_rel_error = true_rel_error_loop end

sin x = x 3! 9! 7! 5