MATLAB MATLAB MATLAB

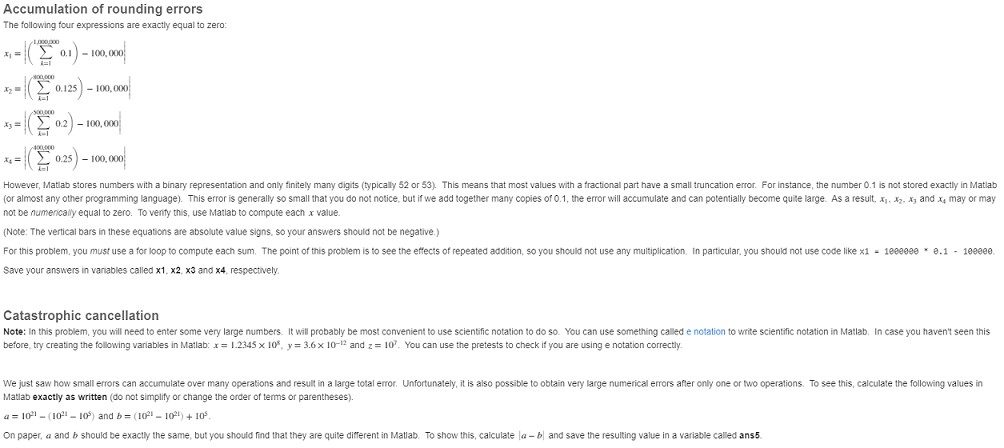
Accumulation of rounding errors The following four expressions are exactly equal to zero x = (10.1) - 10.00 - 0.125) 100.0 5,= ( *02) - 10,00 x = ( *025) - 100.0 However, Matlab stores numbers with a binary representation and only finitely many digits (typically 52 or 53). This means that most values with a fractional part have a small truncation error. For instance, the number 0.1 is not stored exactly in Matlab (or almost any other programming language). This error is generally so small that you do not notice, but if we add together many copies of 0.1, the error will accumulate and can potentially become quite large. As a result, xy 12, A, and may or may not be numerically equal to zero. To venty this, use Matlab to compute each x value. (Note: The vertical bars in these equations are absolute value signs, so your answers should not be negative) For this problem, you must use a for loop to compute each sum. The point of this problem is to see the effects of repeated addition, so you should not use any multiplication in particular, you should not use code like x1 - 1eeeeee * 0.1 - 1eeeee Save your answers in vanables called x1, x2, x3 and x4, respectively Catastrophic cancellation Note: In this problem, you will need to enter some very large numbers. It will probably be most convenient to use scientific notation to do so. You can use something called e notation to write scientific notation in Matlab. In case you haven't seen this before try creating the following variables in Matlab: x = 1.2345 x 10%, y = 3.6 x 10-12 and 2 = 10'. You can use the pretests to check if you are using e notation correctly We just saw how small errors can accumulate over many operations and result in a large total error. Unfortunately, it is also possible to obtain very large numerical errors after only one or two operations. To see this, calculate the following values in Matlab exactly as written (do not simplify or change the order of terms or parentheses). a = 10% - 10%-10%) and b = (10%-10%) + 10% On paper, a and b should be exactly the same, but you should find that they are quite different in Matlab. To show this, calculate - bl and save the resulting value in a variable called ans5