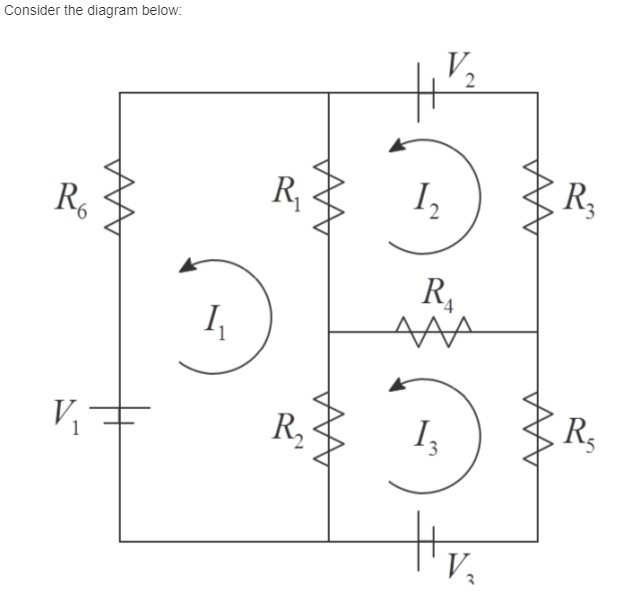
MATLAB MATLAB MATLAB

Consider the diagram below V R$ Here, each V represents a change in voltage (in volts) at a battery, each R represents a resistance in ohms) at a resistor and each I represents a current (in amps) through a wire. These quantities obey two simple laws: 1. Ohm's law: The voltage drop across a resistor is V = IR. 2. Kirchhoff's second law: The sum of all the voltage changes in a closed loop is zero. Using these two laws, we can construct the following system of equations: RI+R, 6-1) + R21-13) = V1 R3/2+R 12-13) +R, 12-1) = V2. R513 + R. (13-1) + R213-1) = Vz. Suppose that the resistances are given by R = 15, R2 = 20, R3 = 6, R. = 18, Rs = 25 and Ro = 30 (all in ohms) and that we are trying to calculate the currents 11, 12 and 13. 1. Write these equations in the matrix form Ax=b, where x is a 3 x 1 vector of unknown currents. You need to do this by hand, not in Matlab. (Note that the equations above are not fully simplified. You can use the pretest to make sure you simplified correctly. Using the lu command in Matlab, find the matrices L, U and P such that LU = PA. Calculate the product UPL and save the resulting matrix in a variable named ans1. (There is no mathematical reason to calculate this matrix - I just want to check that you found all three matrices.) Notice that I haven't told you the voltages yet. Do you need them? 2. We will now fix everything except V3 and see how the current changes with voltage: Let V = 60 and V2 = 50. For every value of V3 from 1 to 100 (in increments of 1) calculate 1, 12 and 13 using the LU decomposition from above. Save your answers in a 3 x 100 matrix named ans2. The ith column of this matrix should contain the vector 1,12,131" that you solved for using V3 = i. 3. Next, we will fix all of the voltages and change one of the resistances. Let Vi = 60, V2 = 50 and V3 = 40 and keep all of the resistances above the same except for R. For every value of R, from 1 to 100 (in increments of 1) calculate 11, 12 and 13 using the backslash command directly. Save your answers in a 3 x 100 matrix named ans3. The ith column of this matrix should contain the vector 1,12,13 that you solved for using R =i. Note that changing R changes more than one entry in A. Also notice that if you reuse the variable name A you will no longer pass the pretest from part 1. This is ok, since the pretest is not worth any points