Answered step by step
Verified Expert Solution
Question
1 Approved Answer
matlab pendulumPlot.m 2 Ordinary differential equations 2.1 Projectile with drag Recall the motion of a projectile calculated in Lab2 2 which corresponds to the (uncoupled
matlab 
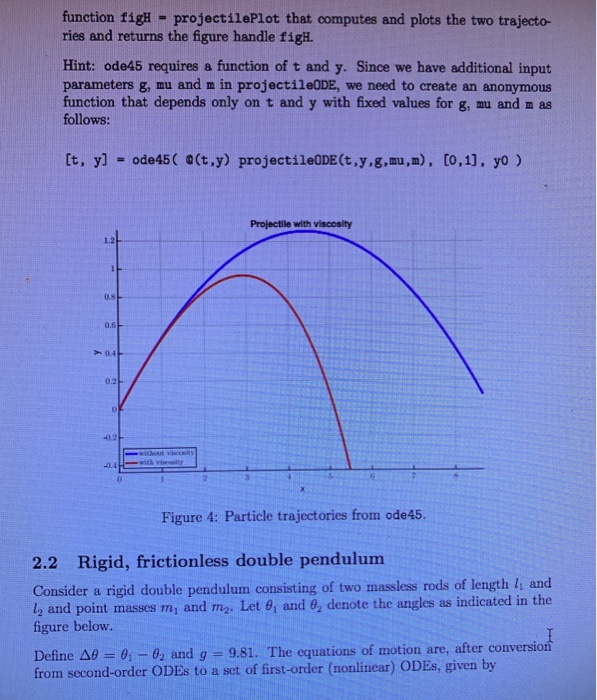
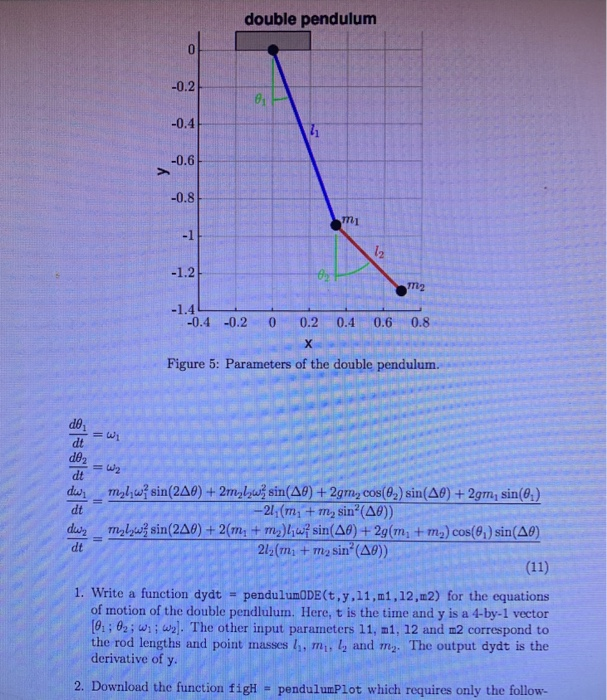
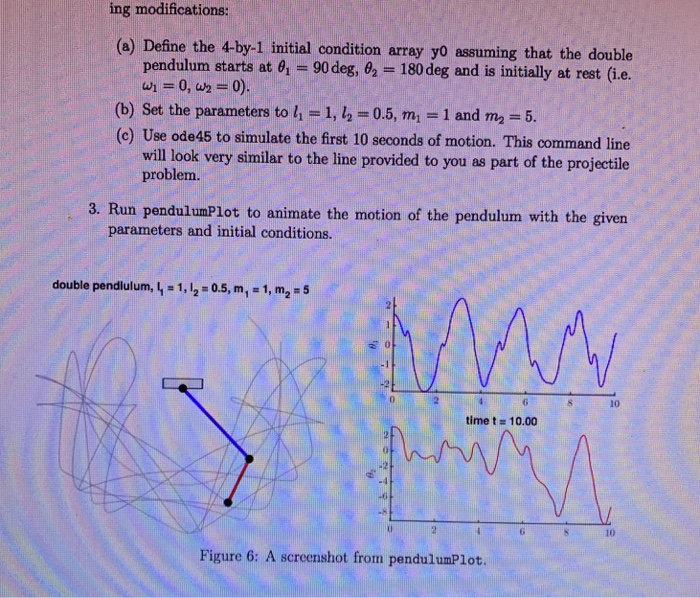
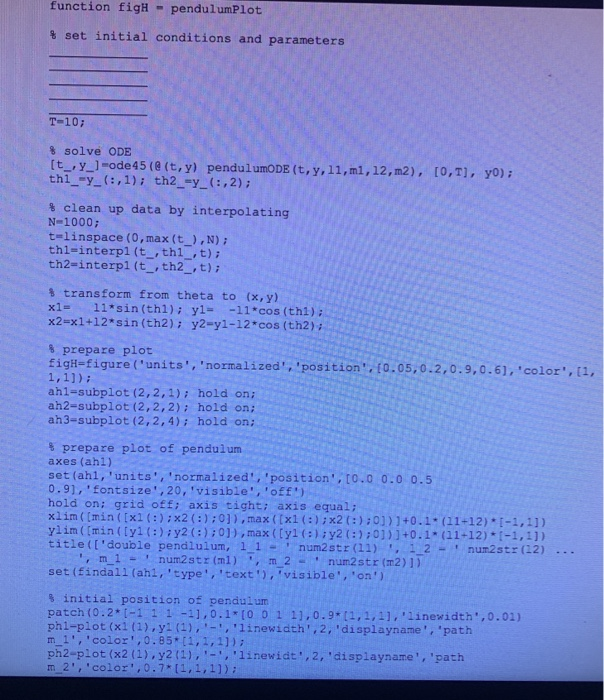
2 Ordinary differential equations 2.1 Projectile with drag Recall the motion of a projectile calculated in Lab2 2 which corresponds to the (uncoupled set of) differential equations d2r du dt2 dt dt2 dt Now let's instead consider the case of a projectile moving through a viscous medium. If the flow around the projectile is laminar the viscous drag Fo is approximately proportional to the velocity with viscosity . The equations of motion are now dz dt dy dt dvz dt duy dt Trt with initial conditions 1. Write a function dydt - projectiledDE(t,y,g,mu,m) for the equations of motion of the projectile. Here, t is the time, y is a 4-by-1 vector ri yi vgi vy and g, au and m correspond to the parameters g, and m. The output dydt is the derivative of y 2. Define the 4-by-1 initial condition array yo assuming that the projectile starts at 0,-: 0 and the initial velocity is vo-10 at an angle -30 deg. 3. Solve the differential equation using ode45 for the first sccond of flight. Con- sider the following two scenarios: In the first, use g-9.81 ms-2, 0 (no viscosity) and m = 1 kg. In the second case, use -1Nsm-1. write a 2 Ordinary differential equations 2.1 Projectile with drag Recall the motion of a projectile calculated in Lab2 2 which corresponds to the (uncoupled set of) differential equations d2r du dt2 dt dt2 dt Now let's instead consider the case of a projectile moving through a viscous medium. If the flow around the projectile is laminar the viscous drag Fo is approximately proportional to the velocity with viscosity . The equations of motion are now dz dt dy dt dvz dt duy dt Trt with initial conditions 1. Write a function dydt - projectiledDE(t,y,g,mu,m) for the equations of motion of the projectile. Here, t is the time, y is a 4-by-1 vector ri yi vgi vy and g, au and m correspond to the parameters g, and m. The output dydt is the derivative of y 2. Define the 4-by-1 initial condition array yo assuming that the projectile starts at 0,-: 0 and the initial velocity is vo-10 at an angle -30 deg. 3. Solve the differential equation using ode45 for the first sccond of flight. Con- sider the following two scenarios: In the first, use g-9.81 ms-2, 0 (no viscosity) and m = 1 kg. In the second case, use -1Nsm-1. write a 



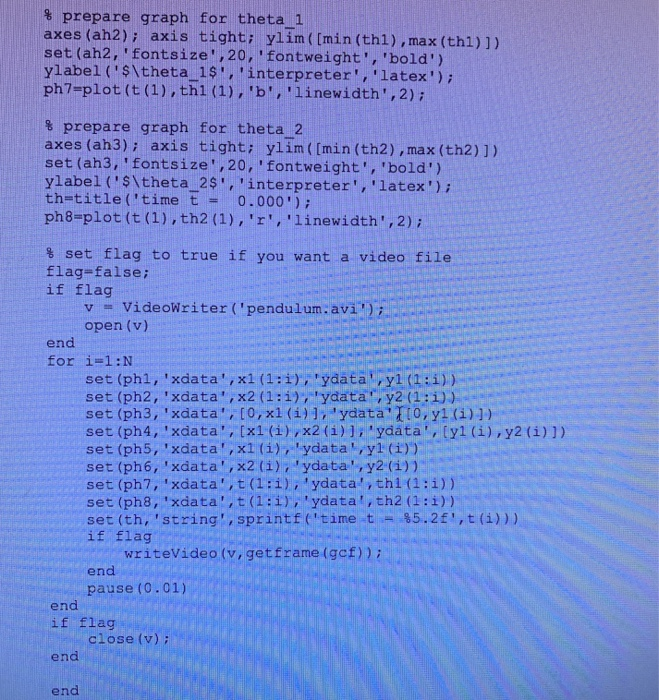
pendulumPlot.m


Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


