matlab

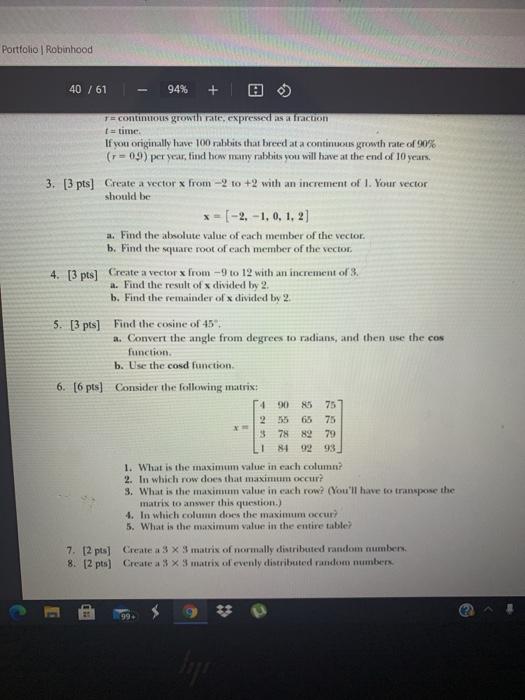
Portfolio | Robinhood 40 / 61 94% + HW 4 (25 pts) 1. [4 pts] MATLAB contains functions to calculate the natural logarithm (10g), the logarithin to the base 10 (log10), and the logarithm to the base 2 (1992). However, if you want to find a logarithm to another base--for example, base byou'll have to do the math yourself with the formula log.(x) log.( x) log. (6) What is the log of 10 when bis defined from 1 to 10 in increments of 1? 2. [2 pts) Populations tend to expand exponentially, that is where P. current population P-original population continuous growth rate, expressed as a as a fraction If you originally howe 100 rabbits that breed at a continuous growth rate of (r= 0.9) per year. Find how many rabbits you will have at the end of 10 years, 3. [3 pts) Create a vector from - to +2 with an increment of 1. Your vector should be *- (-2-1, 0.1.2] a. Find the absolute value of each member of the vector b. Find the square root of each member of the vector 4. (3 pts) Create a vector from 9 to 12 with an increment of 3. a. Find the result of s divided by 2. b. Find the remainder of divided by 2 5. [3 pts) Find the cosine of 45 3. Convert the angle from degrees to radians, and then use the cos function b. Use the cond function. 6. [6 pts) Consider the following matris Portfolio | Robinhood 40 / 61 94% + T= continuous growth rate, expressed as a fraction t=time. If you originally have 100 rabbits that breed at a continuous growth rate of 90% (r=09) per year, tind how many rabbits you will have at the end of 10 years. 3. [3 pts) Create a vector from 2 10 +2 with an increment of I. Your vector should be * = [-2. -1, 0, 1, 2) .. Find the absolute value of each member of the vector b. Find the square root of each member of the vector 4. [3 pts] Create a vector x from -9 to 12 with an increment of a. Find the result of x divided by 2. b. Find the remainder of divided by 2. 5. [3 pts) Find the cosine of 45 a. Convert the angle from degrees to radians, and then use the cos function b. Use the cosd function 6. [6 pts] Consider the following matris: 400 75 23565 75 378 89 79 84 92 93 1. What is the maximum value in each column? 2. In which row does that maximum occur? 3. What is the maximum value in each row? (You'll have to transpose the matrix to answer this question.) 4. In which column does the maximum occur 5. What is the maximum value in the entire table? 7. 12 pts] Create a 3 x 3 matrix of normally distributed random numbers 8. 12 pts) Create a 3 x 3 matrix of evenly distributed random numbers