Matlab question, I will add the runge kutta function to this post. I'm just not sure how to implement with three equations that rely on each other, rather than just one F(t,y).

Problem 2: The goal of this problem is to explore the concept of stability in the solution of a stiff system of ODEs. The following system is a classic example of a stiff system of ODEs that commonly occur in the simulation of chemical reaction kinetics:

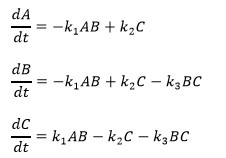
Where A, B and C represent the concentrations of three chemical species and the k constants are the reaction rates for the reactions involved in the chemical mechanism. Solve these equations from t = 0 to 12 using the following methods. Use initial conditions of A(0) = 1, B(0) = 2.2 and C(0) = 0 and rate constants of k1 = 0.15, k2 = 0.1, and k3 = 120. For each of the 5 solutions, save your solution in a 3 column matrix with the first column the concentration of A, the second column the concentration of B, and the third column the concentration of C.

a) Use 4th Order Runge-Kutta (odeRK4sys.m) with h = 0.02. You should notice this solution goes unstable and blows up relatively quickly as the solution steps forward in time.

b) Use 4th Order Runge-Kutta (odeRK4sys.m) with h = 0.015. You should notice this solution goes unstable but recovers as the solution steps forward in time. The instability leads to wildly inaccurate results for C but recovers to stable behavior going forward in time. But is it accurate?

c) Use 4th Order Runge-Kutta (odeRK4sys.m) with h = 0.01. You should get a stable solution. How does the accuracy compare to the solution for part (g)? How would you classify the stability of RK4 applied to this system of odes?

d) Use ode45 with AbsTol and RelTol both set to 10-6. Let MATLAB choose the step size using the adaptive time stepping built in to ode45.

e) Use ode23s with AbsTol and RelTol both set to 10-6. Let MATLAB choose the step size using the adaptive time stepping built in to ode23s.

f) Use the diff and mean functions together to calculate the average step sizes taken by ode45 and ode23s in parts d and e respectively. Save these results in a two-element row vector.

odeRK4sys.m

function [t,y] = odeRK4sys(dydt,tspan,y0,h,varargin) % fourth-order Runge-Kutta for a system of ODEs % [t,y] = oderk4sys(dydt,tspan,y0,h,p1,p2,...): integrates a % system of ODEs with classical fourth-order Runge-Kutta % inputs % dydt = name of the function that evaluates the ODEs % tspan = [ti, tf]; initial and final times with output % generated at interval of h, or % y0 = initial values of dependent variables (row vector) % h = step size % p1,p2,... = additional parameters used by dydt % outputs % % t = vector of independent variable % y = vector of solution for dependent variables

if nargin dA dt dB dt dc dt Ki4