May you explain all , how was these equations derived and how to tackle these kind of questions,, or I cant vote, thanks , and especially the diagram!;;

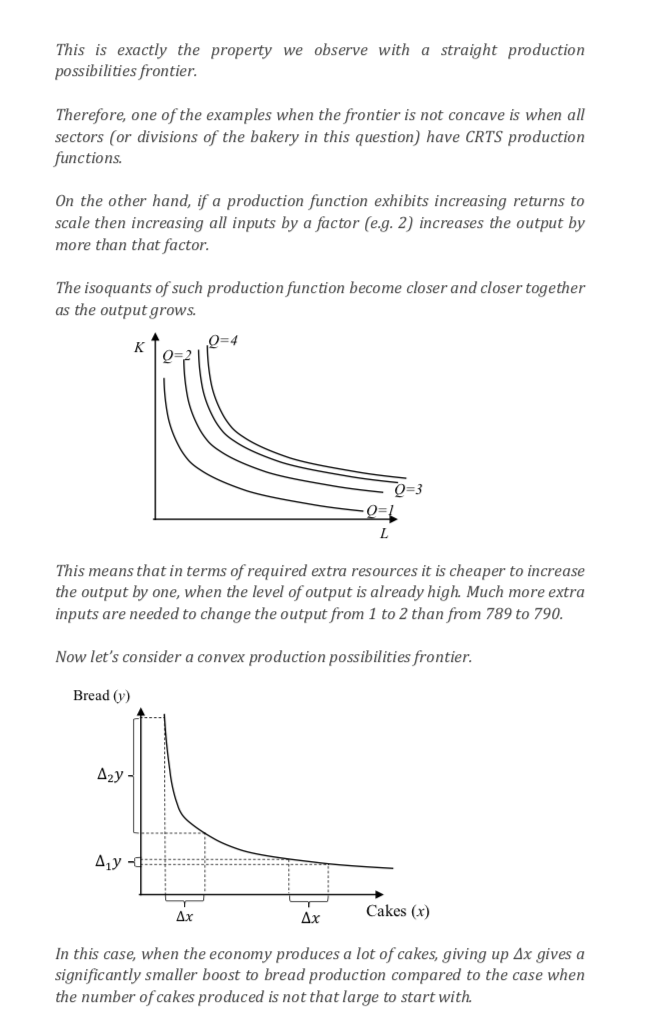
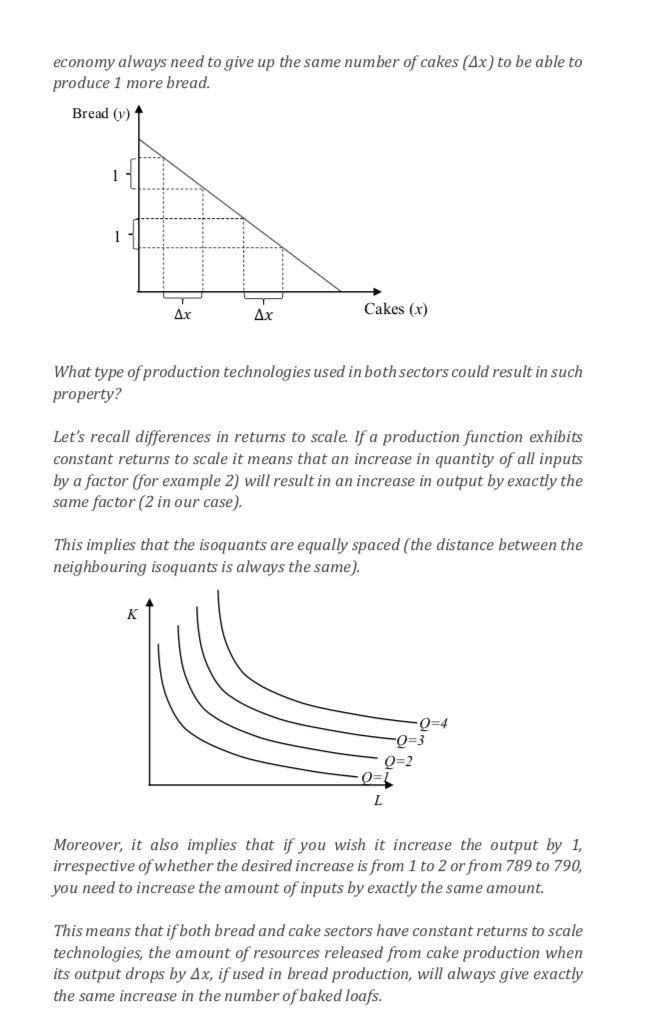
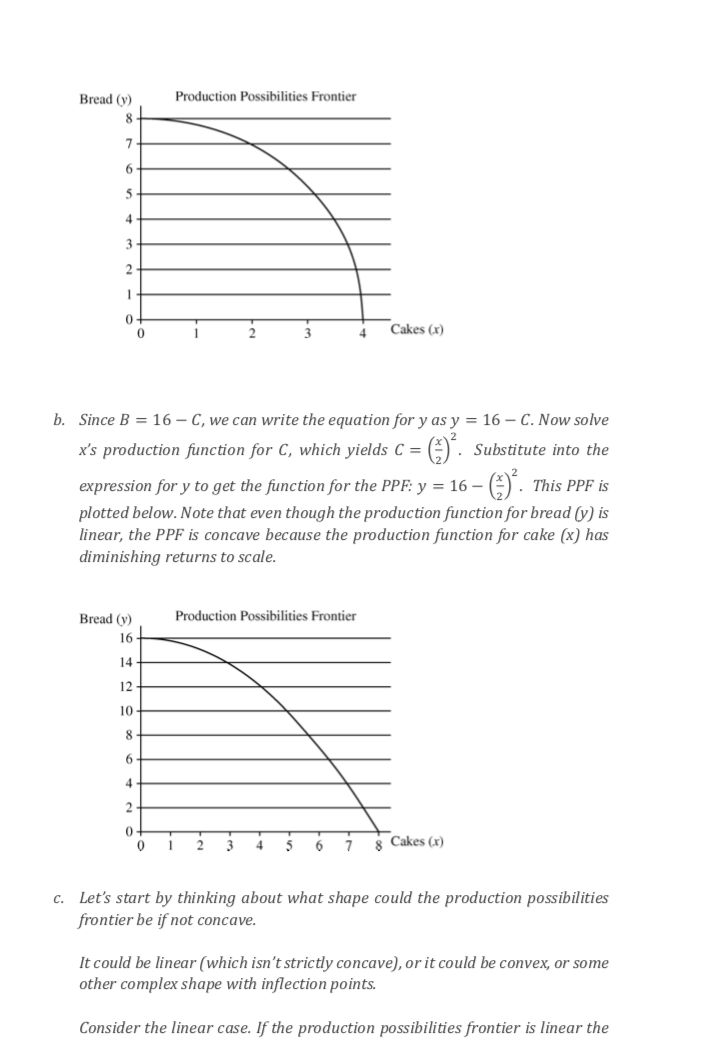
This is consistent with the production in both sectors exhibiting increasing returns to scale. Assume that both cakes and bread are made using IRTS technology. When many cakes are made, the reduction of their production by Ax does not release large amount of inputs. This is because very few extra inputs were required in the first place to make those Ax cakes. The released inputs, nevertheless, do allow to make A, y more bread. However, when very few cakes are made, a reduction in their productions releases relatively large amounts of resources. And this allows to increase bread production by a significantly larger amount 4 2y. Thus, the case when both sectors use IRTS production is another example of a non-concave production possibilities frontier. You can apply the same logic to come up with more examples e.g. one sector with IRTS and the other one with CRTS or even DRTS.This is exactly the property we observe with a straight production possibilities frontier. Therefore, one of the examples when the frontier is not concave is when all sectors (or divisions of the bakery in this question) have CRTS production functions. On the other hand, if a production function exhibits increasing returns to scale then increasing all inputs by a factor (e.g. 2) increases the output by more than that factor. The isoquants of such production function become closer and closer together as the output grows. K 0=4 L This means that in terms of required extra resources it is cheaper to increase the output by one, when the level of output is already high. Much more extra inputs are needed to change the output from 1 to 2 than from 789 to 790. Now let's consider a convex production possibilities frontier. Bread (y) Azy - Ax Ax Cakes (x) In this case, when the economy produces a lot of cakes, giving up Ax gives a significantly smaller boost to bread production compared to the case when the number of cakes produced is not that large to start with.economy always need to give up the same number of cakes (4x) to be able to produce 1 more bread. Bread (v) + Ax Ax Cakes (x) What type of production technologies used in both sectors could result in such property? Let's recall differences in returns to scale. If a production function exhibits constant returns to scale it means that an increase in quantity of all inputs by a factor (for example 2) will result in an increase in output by exactly the same factor (2 in our case). This implies that the isoquants are equally spaced (the distance between the neighbouring isoquants is always the same). K 0=4 0=3 0=2 L Moreover, it also implies that if you wish it increase the output by 1, irrespective of whether the desired increase is from 1 to 2 or from 789 to 790, you need to increase the amount of inputs by exactly the same amount. This means that if both bread and cake sectors have constant returns to scale technologies, the amount of resources released from cake production when its output drops by Ax, if used in bread production, will always give exactly the same increase in the number of baked loafs.Bread (y) Production Possibilities Frontier 5 4 3 Cakes (x) b. Since B = 16 - C, we can write the equation for y as y = 16 - C. Now solve x's production function for C, which yields C = (C) . Substitute into the expression for y to get the function for the PPF: y = 16 - (@) . This PPF is plotted below. Note that even though the production function for bread (y) is linear, the PPF is concave because the production function for cake (x) has diminishing returns to scale. Bread (y) Production Possibilities Frontier 16- 14 12 - 10 8 g Cakes (x) c. Let's start by thinking about what shape could the production possibilities frontier be if not concave. It could be linear (which isn't strictly concave), or it could be convex, or some other complex shape with inflection points. Consider the linear case. If the production possibilities frontier is linear theSuppose a bakery has 16 employees to be designated as bread bakers (B) and cake bakers (C), so that B + C = 16. Draw the production possibilities frontier for bread [y] and cakes [x] for the following production functions: a. y = 23'5 andx = C"'5 b. y = B andx = 2C"-5 c. Give an example of conditions when the production possibilities frontier might not be concave. ANSWER: a. Since B = 16 C, we can write y = 2(16 C)'5. And since 2: = Cc"5 it follows that C = x2. Substituting for C in the expression for y, we get y = 2(16 x2)'5, which can also be written as y2 + 4x2 = 64. This is the equation for the PPF. The shape is an ellipse. Calculate intersection with axes: y = 0 (it x = 4. x = 0 (it y = 8. The plot of the PPF is given in the diagram below. it has the usual concave shape