MBA: Coroporate finace

Textbook: Brigham, E. F., & Ehrhardt, M. C. (2020). Financial management: Theory and practice (16th ed.). Thomson South-Western. ISBN-13: 978-1-337-90260-1.

Chapter 4, problem 35 (Build a Model: the time Value of Money)

Answer the following questions, using the spreadsheet model to do the calculations. a. Find the FV of $1,000 invested to earn 10% annually 5 years from now. Answer this question first by using a math formula and then by using the Excel function wizard. b. Now create a table that shows the FV at 0%, 5%, and 20% for 0, 1, 2, 3, 4, and 5 years. Then create a graph with years on the horizontal axis and FV on the vertical axis to display your results. c. Find the PV of $1,000 due in 5 years if the discount rate is 10% per year. Again, first work the problem with a formula and then by using the function wizard. d. A security has a cost of $1,000 and will return $2,000 after 5 years. What rate of return does the security provide? e. Suppose Californias population is 30 million people and its population is expected to grow by 2% per year. How long would it take for the population to double? f. Find the PV of an ordinary annuity that pays $1,000 at the end of each of the next 5 years if the interest rate is 15%. Then find the FV of that same annuity. g. How would the PV and FV of the above annuity change if it were an annuity due rather than an ordinary annuity? h. What would the FV and PV for parts a and c be if the interest rate were 10% with semiannual compounding rather than 10% with annual compounding? i. Find the PV and FV of an investment that makes the following end-of-year pay- ments. The interest rate is 8%. Year Payment 1 $100 2 200 3 400 j. Suppose you bought a house and took out a mortgage for $50,000. The interest rate is 8%, and you must amortize the loan over 10 years with equal end-of-year pay- ments. Set up an amortization schedule that shows the annual payments and the amount of each payment that repays the principal and the amount that constitutes interest expense to the borrower and interest income to the lender. (1) Create a graph that shows how the payments are divided between interest and principal repayment over time. (2) Suppose the loan called for 10 years of monthly payments, 120 payments in all, with the same original amount and the same nominal interest rate. What would the amortization schedule show now?

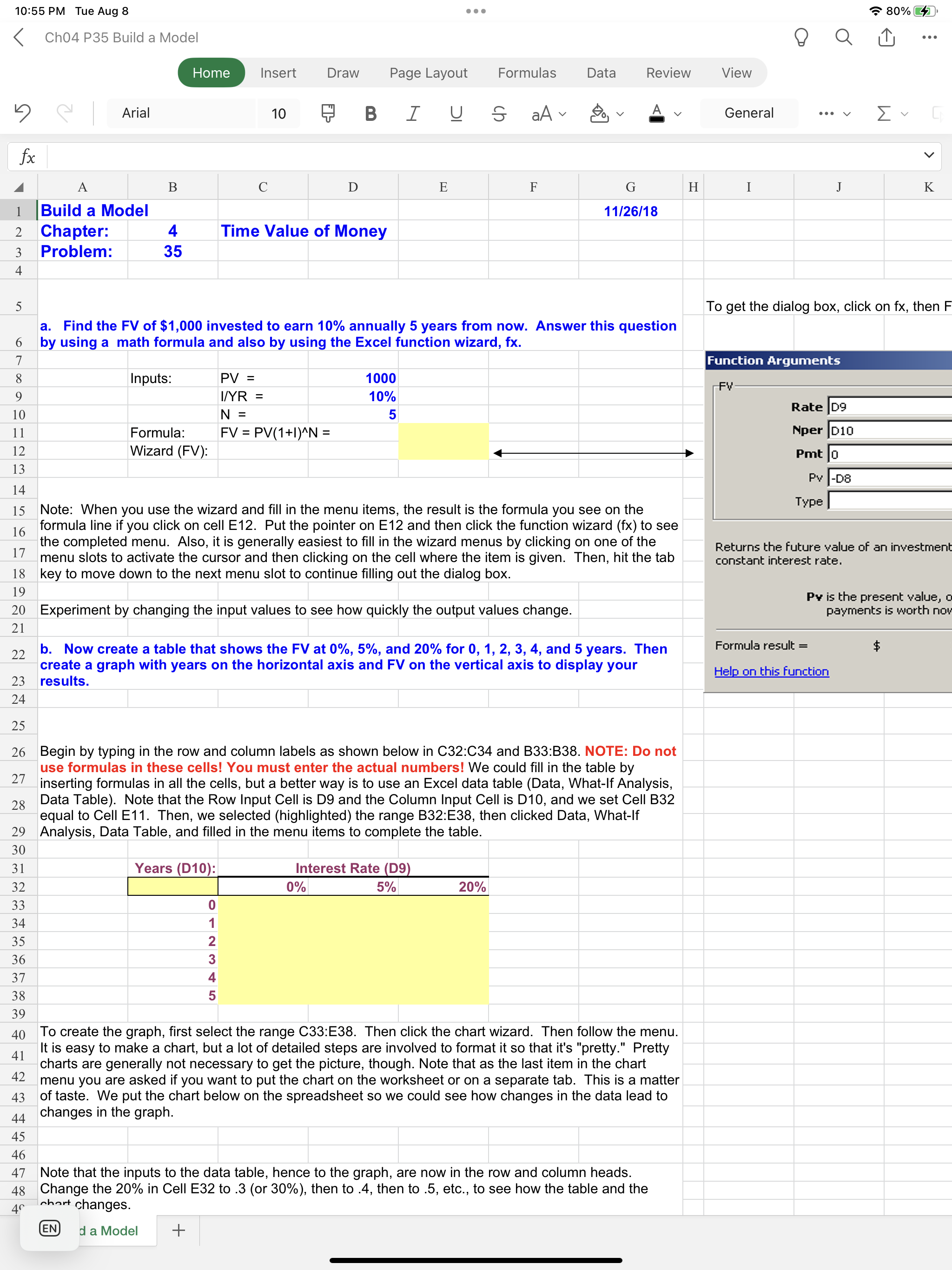
8

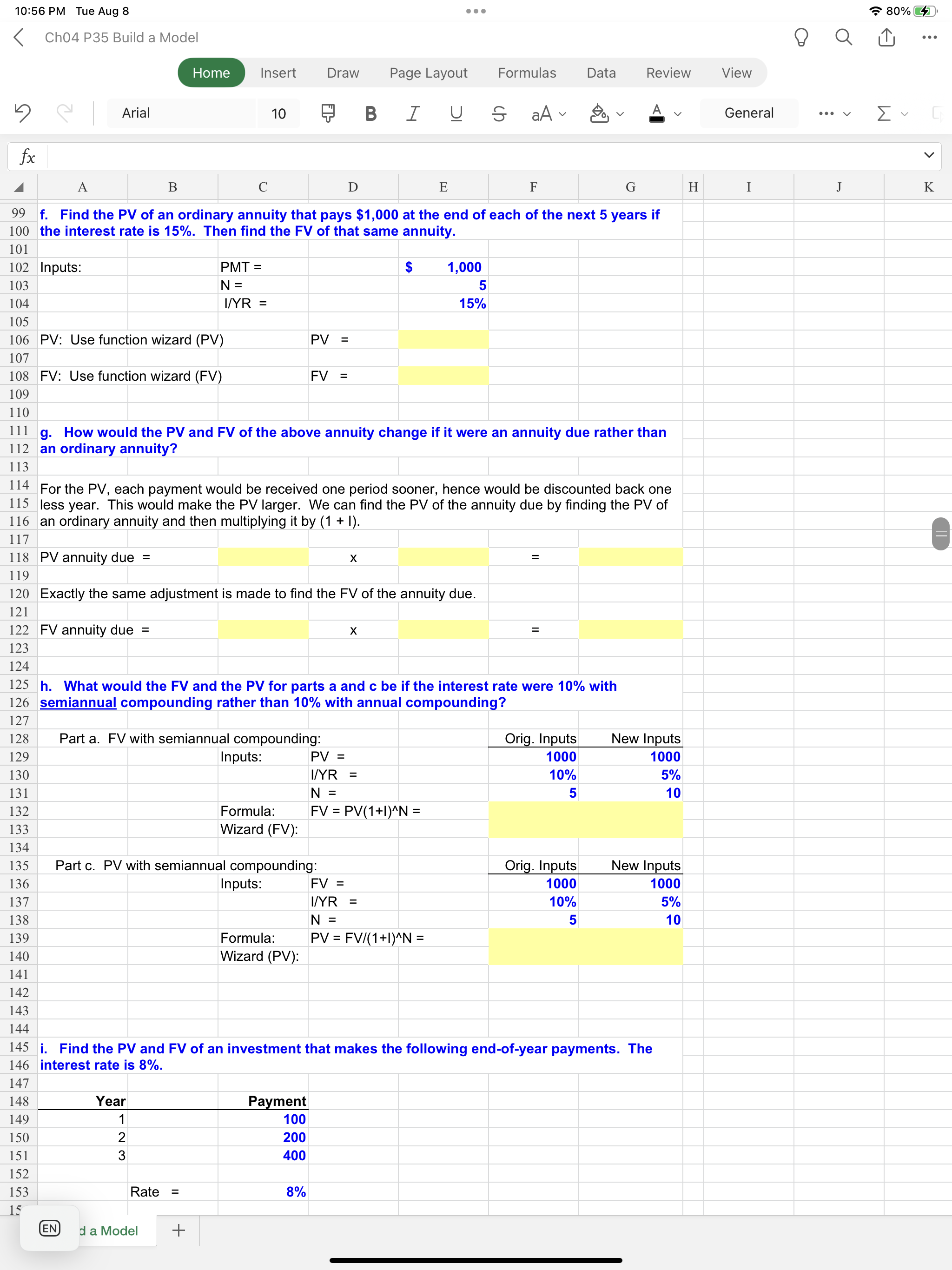
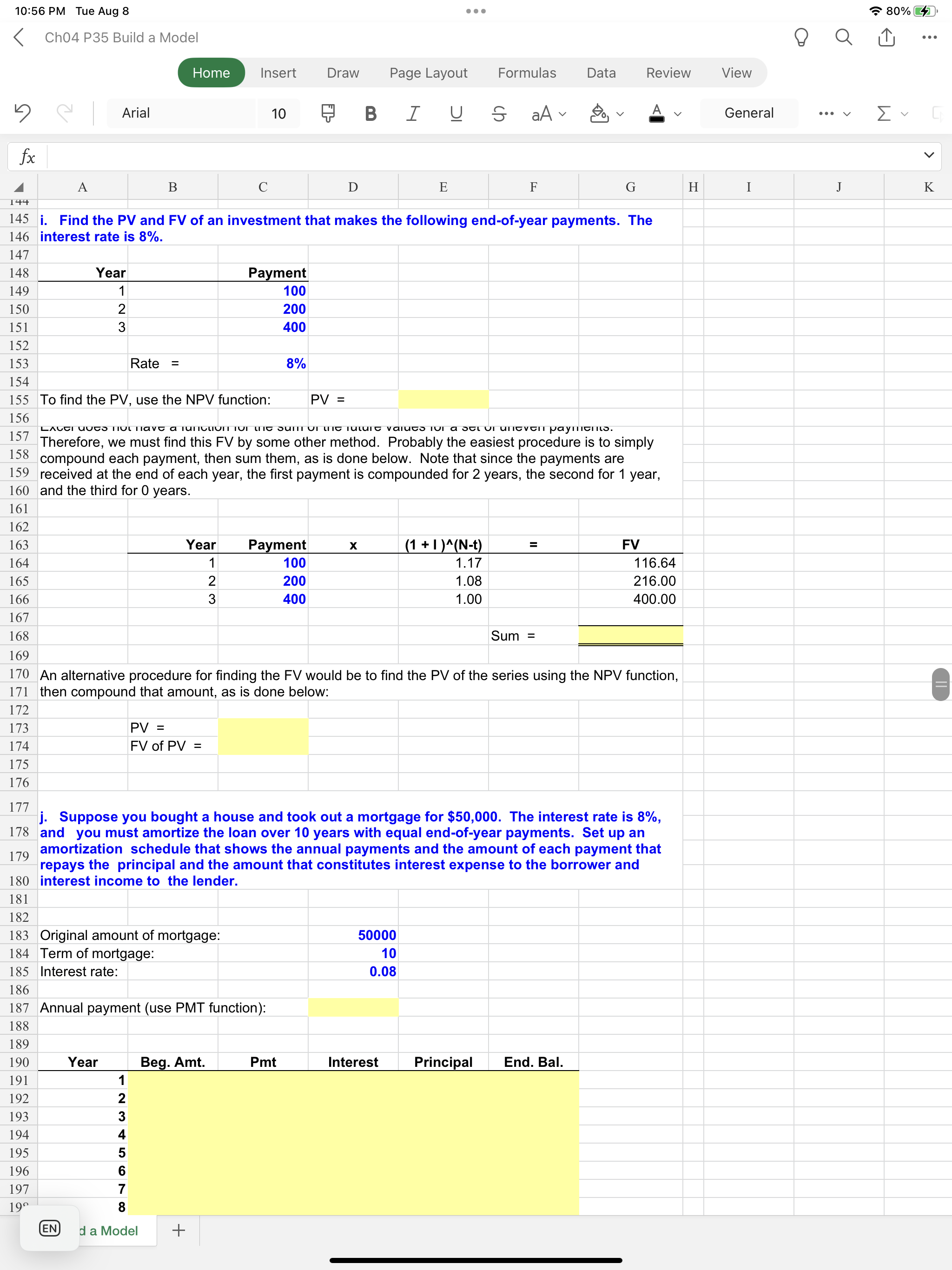
10:57 PM Tue Aug 8 \\( 8, and you must amortize the loan over 10 years with equal end-of-year payments. Set up an amortization schedule that shows the annual payments and the amount of each payment that repays the principal and the amount that constitutes interest expense to the borrower and interest income to the lender. 10:56 PM Tue Aug 8 Ch04 P35 Build a Model Home Insert Page Layout Formulas Data Review View \u0E56 \\( \\quad \\) Arial 10 \u091C B I \\( \\underline{\\cup} \\subseteq a \\mathrm{aA} \\sim \\otimes_{0} \\vee \\) General 10:55 PM Tue Aug 8 Ch04 P35 Build a Model Home Insert Draw Page Layout Formulas Data Review View \u0E53 Arial 10 B I \\( \\mathrm{aA} \\vee \\otimes_{0} \\vee \\) A General \\( f x \\) 14 15 Note: When you use the wizard and fill in the menu items, the result is the formula you see on the formula line if you click on cell E12. Put the pointer on E12 and then click the function wizard (fx) to see the completed menu. Also, it is generally easiest to fill in the wizard menus by clicking on one of the menu slots to activate the cursor and then clicking on the cell where the item is given. Then, hit the tab key to move down to the next menu slot to continue filling out the dialog box. Experiment by changing the input values to see how quickly the output values change. b. Now create a table that shows the FV at \0, and \20 for \\( 0,1,2,3,4 \\), and 5 years. Then create a graph with years on the horizontal axis and FV on the vertical axis to display your results. To get the dialog box, click on fx, then F Function Arguments Returns the future value of an investment constant interest rate. Py is the present value, o payments is worth nov Formula result \\( = \\) Help on this function Begin by typing in the row and column labels as shown below in C32:C34 and B33:B38. NOTE: Do not use formulas in these cells! You must enter the actual numbers! We could fill in the table by inserting formulas in all the cells, but a better way is to use an Excel data table (Data, What-If Analysis, Data Table). Note that the Row Input Cell is D9 and the Column Input Cell is D10, and we set Cell B32 equal to Cell E11. Then, we selected (highlighted) the range B32:E38, then clicked Data, What-If Analysis, Data Table, and filled in the menu items to complete the table. 30 31 To create the graph, first select the range C33:E38. Then click the chart wizard. Then follow the menu. It is easy to make a chart, but a lot of detailed steps are involved to format it so that it's \"pretty.\" Pretty charts are generally not necessary to get the picture, though. Note that as the last item in the chart menu you are asked if you want to put the chart on the worksheet or on a separate tab. This is a matter of taste. We put the chart below on the spreadsheet so we could see how changes in the data lead to changes in the graph. Note that the inputs to the data table, hence to the graph, are now in the row and column heads. Change the \20 in Cell E32 to 3 (or \30 ), then to .4, then to .5 , etc., to see how the table and the nhart changes. EN \\( d \\) a Model \\( + \\) 10:56 PM Tue Aug 8 Ch04 P35 Build a Model Home Insert Draw Page Layout Formulas Data Review View \u308A Arial 10 B \\( \\quad I \\quad \\underline{U} \\quad \\mathcal{S} \\) \\( \\mathrm{aA} \\vee \\otimes_{0} v \\) A General \\( f x \\) A B C D E G H I J K 99 f. Find the PV of an ordinary annuity that pays \\( \\$ 1,000 \\) at the end of each of the next 5 years if 100 the interest rate is \15. Then find the \\( F V \\) of that same annuity. 101 102 Inputs: \\( \\mathrm{PMT}= \\) \\( \\mathrm{N}= \\) \\( \\mathrm{I} / \\mathrm{YR}= \\) PV: Use function wizard (PV) \\( \\mathrm{PV}= \\) FV: Use function wizard (FV) \\( \\mathrm{FV}= \\) g. How would the PV and FV of the above annuity change if it were an annuity due rather than an ordinary annuity? For the PV, each payment would be received one period sooner, hence would be discounted back one less year. This would make the PV larger. We can find the PV of the annuity due by finding the PV of an ordinary annuity and then multiplying it by \\( (1+I) \\). 117 118 PV annuity due = \\( \\mathrm{x} \\) 120 Exactly the same adjustment is made to find the FV of the annuity due. 121 122 FV annuity due = \\( \\mathrm{x} \\) 123 124 125 h. What would the FV and the PV for parts a and \\( \\mathrm{c} \\) be if the interest rate were \10 with 126 semiannual compounding rather than \10 with annual compounding? 127 128 Part a. FV with semiannual compounding: 129 130 Inputs: \\( \\mathrm{PV}= \\) \\( \\mathrm{I} / \\mathrm{YR}= \\) \\( \\mathrm{N}= \\) Formula: \\( \\quad \\mathrm{FV}=\\mathrm{PV}(1+\\mathrm{I})^{\\wedge} \\mathrm{N}= \\) Wizard (FV): Part c. PV with semiannual compounding: Inputs: \\( \\mathrm{FV}= \\) \\( \\mathrm{I} / \\mathrm{YR}= \\) \\( \\mathrm{N}= \\) Formula: \\( \\quad \\mathrm{PV}=\\mathrm{FV} /(1+\\mathrm{I})^{\\wedge} \\mathrm{N}= \\) Wizard (PV): \\begin{tabular}{|r|r|} \\hline Orig. Inputs & New Inputs \\\\ \\hline 1000 & 1000 \\\\ \10 & \5 \\\\ 5 & 10 \\end{tabular} \\begin{tabular}{|r|r|} \\hline Orig. Inputs & New Inputs \\\\ \\hline 1000 & 1000 \\\\ \10 & \5 \\\\ \\hline 5 & 10 \\end{tabular} i. Find the PV and FV of an investment that makes the following end-of-year payments. The interest rate is \8. \\begin{tabular}{|r|r|r|} \\hline 147 & & \\\\ \\hline 148 & Year & Payment \\\\ \\cline { 2 - 3 } & 149 & \\( \\mathbf{1 0 0} \\) \\\\ \\hline 150 & 2 & \\( \\mathbf{2 0 0} \\) \\\\ \\hline 151 & 3 & \\( \\mathbf{4 0 0} \\) \\\\ \\hline 152 & & \\\\ \\hline 153 & Rate \\( = \\) & \\( \\mathbf{8 \\%} \\) \\\\ \\hline 15 & & \\end{tabular} EN \\( d \\) a Model + 10:57 PM Tue Aug 8 \\( 8, and you must amortize the loan over 10 years with equal end-of-year payments. Set up an amortization schedule that shows the annual payments and the amount of each payment that repays the principal and the amount that constitutes interest expense to the borrower and interest income to the lender. 10:56 PM Tue Aug 8 Ch04 P35 Build a Model Home Insert Page Layout Formulas Data Review View \u0E56 \\( \\quad \\) Arial 10 \u091C B I \\( \\underline{\\cup} \\subseteq a \\mathrm{aA} \\sim \\otimes_{0} \\vee \\) General 10:55 PM Tue Aug 8 Ch04 P35 Build a Model Home Insert Draw Page Layout Formulas Data Review View \u0E53 Arial 10 B I \\( \\mathrm{aA} \\vee \\otimes_{0} \\vee \\) A General \\( f x \\) 14 15 Note: When you use the wizard and fill in the menu items, the result is the formula you see on the formula line if you click on cell E12. Put the pointer on E12 and then click the function wizard (fx) to see the completed menu. Also, it is generally easiest to fill in the wizard menus by clicking on one of the menu slots to activate the cursor and then clicking on the cell where the item is given. Then, hit the tab key to move down to the next menu slot to continue filling out the dialog box. Experiment by changing the input values to see how quickly the output values change. b. Now create a table that shows the FV at \0, and \20 for \\( 0,1,2,3,4 \\), and 5 years. Then create a graph with years on the horizontal axis and FV on the vertical axis to display your results. To get the dialog box, click on fx, then F Function Arguments Returns the future value of an investment constant interest rate. Py is the present value, o payments is worth nov Formula result \\( = \\) Help on this function Begin by typing in the row and column labels as shown below in C32:C34 and B33:B38. NOTE: Do not use formulas in these cells! You must enter the actual numbers! We could fill in the table by inserting formulas in all the cells, but a better way is to use an Excel data table (Data, What-If Analysis, Data Table). Note that the Row Input Cell is D9 and the Column Input Cell is D10, and we set Cell B32 equal to Cell E11. Then, we selected (highlighted) the range B32:E38, then clicked Data, What-If Analysis, Data Table, and filled in the menu items to complete the table. 30 31 To create the graph, first select the range C33:E38. Then click the chart wizard. Then follow the menu. It is easy to make a chart, but a lot of detailed steps are involved to format it so that it's \"pretty.\" Pretty charts are generally not necessary to get the picture, though. Note that as the last item in the chart menu you are asked if you want to put the chart on the worksheet or on a separate tab. This is a matter of taste. We put the chart below on the spreadsheet so we could see how changes in the data lead to changes in the graph. Note that the inputs to the data table, hence to the graph, are now in the row and column heads. Change the \20 in Cell E32 to 3 (or \30 ), then to .4, then to .5 , etc., to see how the table and the nhart changes. EN \\( d \\) a Model \\( + \\) 10:56 PM Tue Aug 8 Ch04 P35 Build a Model Home Insert Draw Page Layout Formulas Data Review View \u308A Arial 10 B \\( \\quad I \\quad \\underline{U} \\quad \\mathcal{S} \\) \\( \\mathrm{aA} \\vee \\otimes_{0} v \\) A General \\( f x \\) A B C D E G H I J K 99 f. Find the PV of an ordinary annuity that pays \\( \\$ 1,000 \\) at the end of each of the next 5 years if 100 the interest rate is \15. Then find the \\( F V \\) of that same annuity. 101 102 Inputs: \\( \\mathrm{PMT}= \\) \\( \\mathrm{N}= \\) \\( \\mathrm{I} / \\mathrm{YR}= \\) PV: Use function wizard (PV) \\( \\mathrm{PV}= \\) FV: Use function wizard (FV) \\( \\mathrm{FV}= \\) g. How would the PV and FV of the above annuity change if it were an annuity due rather than an ordinary annuity? For the PV, each payment would be received one period sooner, hence would be discounted back one less year. This would make the PV larger. We can find the PV of the annuity due by finding the PV of an ordinary annuity and then multiplying it by \\( (1+I) \\). 117 118 PV annuity due = \\( \\mathrm{x} \\) 120 Exactly the same adjustment is made to find the FV of the annuity due. 121 122 FV annuity due = \\( \\mathrm{x} \\) 123 124 125 h. What would the FV and the PV for parts a and \\( \\mathrm{c} \\) be if the interest rate were \10 with 126 semiannual compounding rather than \10 with annual compounding? 127 128 Part a. FV with semiannual compounding: 129 130 Inputs: \\( \\mathrm{PV}= \\) \\( \\mathrm{I} / \\mathrm{YR}= \\) \\( \\mathrm{N}= \\) Formula: \\( \\quad \\mathrm{FV}=\\mathrm{PV}(1+\\mathrm{I})^{\\wedge} \\mathrm{N}= \\) Wizard (FV): Part c. PV with semiannual compounding: Inputs: \\( \\mathrm{FV}= \\) \\( \\mathrm{I} / \\mathrm{YR}= \\) \\( \\mathrm{N}= \\) Formula: \\( \\quad \\mathrm{PV}=\\mathrm{FV} /(1+\\mathrm{I})^{\\wedge} \\mathrm{N}= \\) Wizard (PV): \\begin{tabular}{|r|r|} \\hline Orig. Inputs & New Inputs \\\\ \\hline 1000 & 1000 \\\\ \10 & \5 \\\\ 5 & 10 \\end{tabular} \\begin{tabular}{|r|r|} \\hline Orig. Inputs & New Inputs \\\\ \\hline 1000 & 1000 \\\\ \10 & \5 \\\\ \\hline 5 & 10 \\end{tabular} i. Find the PV and FV of an investment that makes the following end-of-year payments. The interest rate is \8. \\begin{tabular}{|r|r|r|} \\hline 147 & & \\\\ \\hline 148 & Year & Payment \\\\ \\cline { 2 - 3 } & 149 & \\( \\mathbf{1 0 0} \\) \\\\ \\hline 150 & 2 & \\( \\mathbf{2 0 0} \\) \\\\ \\hline 151 & 3 & \\( \\mathbf{4 0 0} \\) \\\\ \\hline 152 & & \\\\ \\hline 153 & Rate \\( = \\) & \\( \\mathbf{8 \\%} \\) \\\\ \\hline 15 & & \\end{tabular} EN \\( d \\) a Model +