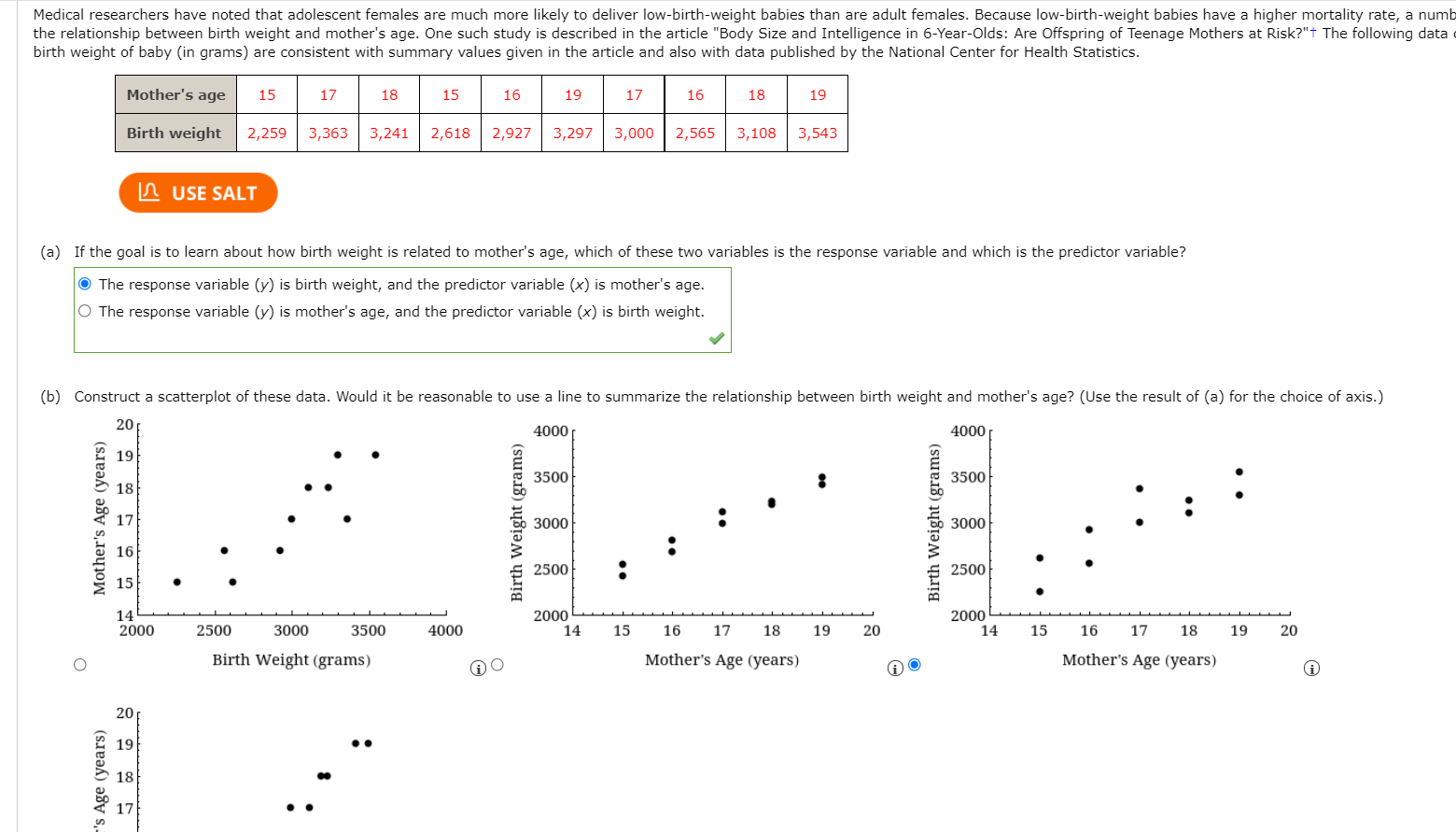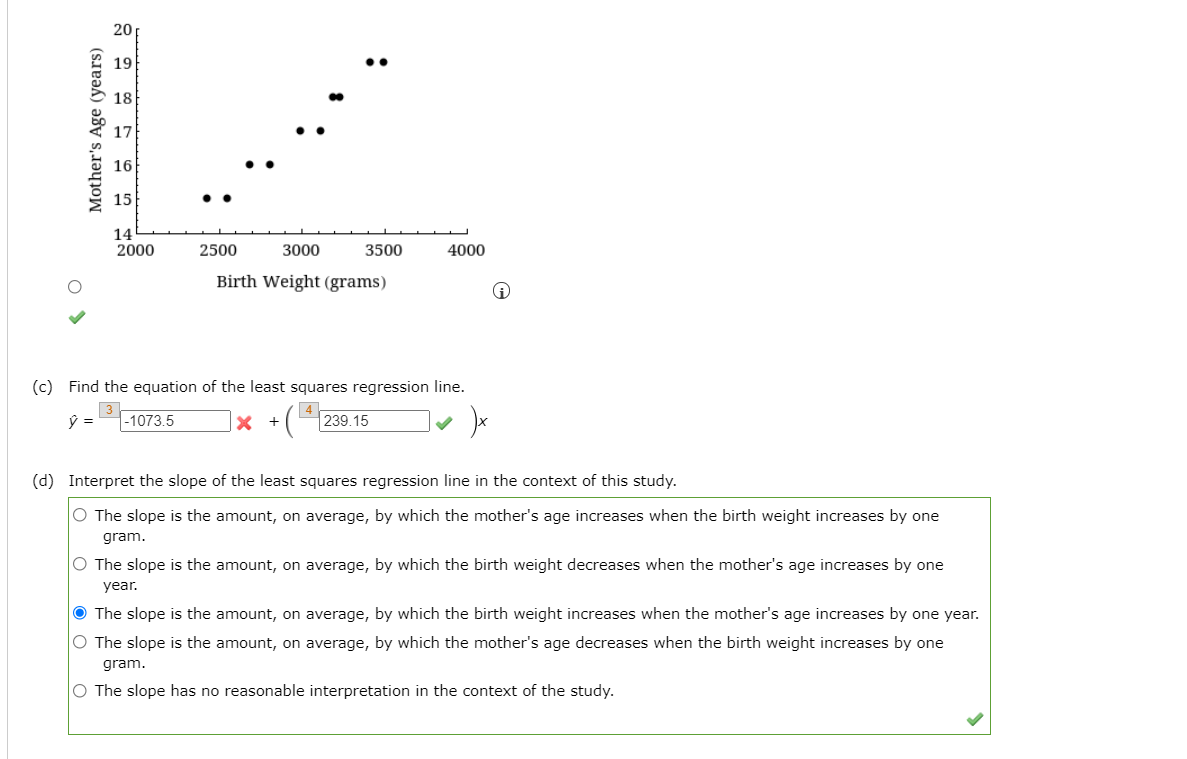
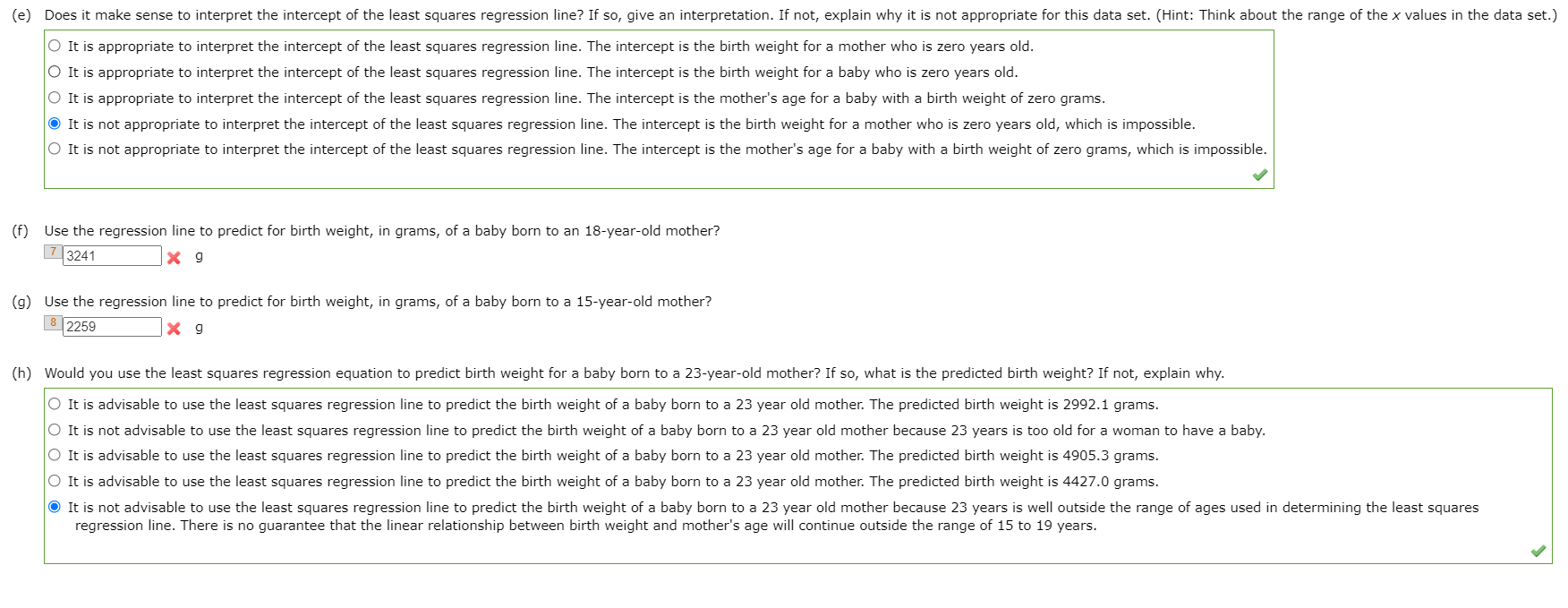
Medical researchers have noted that adolescent females are much more likely to deliver lowebirtheweight babies than are adult females. Because lowebirtheweight babies have a higher mortality rate, a numb the relationship between birth weight and mother's age. One such study is described in the article "Body Size and Intelligenoe in 67Year70|ds: Are Offspring of Teenage Mothers at Risk?\" The following data r birth weight of baby (in grams) are consistent with summary values given in the article and also with data published by the National Center for Health Statistics. Hodler's age 15 17 18 15 16 19 17 16 18 19 2,618 2,927 3,297 3,000 2,565 3,100 3,543 Birlhweight 2,259 3,363 3,241 I0 use SALT (a) If the goal is to learn about how birth weight is related to mother's age, which of these two variables is the response variable and which is the predictor variable? The response variable (y) is birth weight, and the predictor variable (x) is mother's age. 0 The response variable (y) is mother's age, and the predictor variable (x) is birth weight. I (b) Construct a scatterplot of these data. Would it be reasonable to use a line to summarize the relationship between birth weight and mother's age? (Use the result of (a) for the choice of axis.) 2" 4000 4000 Q ._ . 5 19 0 ' E E . 513 o. 53:\" ' 535m 0 ' . I' E i E 3? 1'? ' ' 3000 : 3000 o ' 1': "J t 'I: ' 3 16 I D 3 t 3 . 5 15 . . E 2500 : g 2500 ' 2 ' ' o :n :n 14 2000 2000 2000 2500 3000 3500 4000 14 15 16 17 18 19 20 14 15 16 17 18 19 20 0 Birth Weight (grams) 0 Mother's Age (yeals) CD @ Mother's Age (yeals) 20 E 19 o o I! ll 5 13 u- I] f? 1'? o o '5\" N O O. H W I-'I-'I-l Gin-103 . I a 0 Mother's Age (years) H u: o . 14 2000 2500 3000 3500 4000 Birth Weight (grams) CD 0 (c) Find the equation of the least squares regression line. 3 4 9: .10?3.5 x +( 239.15 .1 )x (d) Interpret the slope of the least squares regression line in the context of this study. O The slope is the amount, on average, by which the mother's age increases when the birth weight increases by one gram. 0 The slope is the amount, on average, by which the birth weight decreases when the mother's age increases by one year. (Q The slope is the amount, on average, by which the birth weight increases when the mother's age increases by one year. 0 The slope is the amount, on average, by which the mother's age decreases when the birth weight increases by one gram. 0 The slope has no reasonable interpretation in the context of the study. (e) Does it make sense to interpret the interoept of the least squares regression line? If so, give an interpretation. If not, explain why it is not appropriate for this data set. (Hint: Think about the range of the x values in the data set.) 0 It is appropriate to interpret the intercept of the least squares regression line. The Intercept is the birth weight for a mother who is zero years old. 0 It is appropriate to interpret the intercept of the least squares regression line. The intercept is the birth weight for a baby who is zero years old. 0 It is appropriate to interpret the intercept of the least squares regression line. The intercept is the mother's age for a baby with a birth weight of zero grams. Q It is not appropriate to interpret the intercept of the least squares regression line. The intercept is the birth weight for a mother who is zero years old, which is impossible. 0 It is not appropriate to interpret the intercept of the least squares regression line. The intercept is the mother's age for a baby with a birth weight of zero grams, which is impossible. I (f) Use the regression line to predict for birth weight, in grams, of a baby born to an 187yeareold mother? 7 2241 x s (9) Use the regression line to predict for birth weight, in grams, of a baby born to a 15-year-old mother? 3 2259 x g (h) Would you use the least squares regression equation to predict birth weight for a baby born to a 23*yeareold mother? If so, what is the predicted birth weight? If not, explain why. 0 It is advisable to use the least squares regression line to predict the birth weight of a baby born to a 23 year old mother. The predicted birth weight is 2992.1 grams. 0 It is not advisable to use the least squares regression line to predict the birth weight of a baby born to a 23 year old mother because 23 years is too old for a woman to have a baby. 0 It is advisable to use the least squares regression line to predict the birth weight of a baby born to a 23 year old mother. The predicted birth weight is 4905.3 grams. 0 It is advisable to use the least squares regression line to predict the birth weight of a baby born to a 23 year old mother. The predicted birth weight is 4427.0 grams. @ It is not advisable to use the least squares regression line to predict the birth weight of a baby born to a 23 year old mother because 23 years is well outside the range of ages used in determining the least squares regression line. There is no guarantee that the linear relationship between birth weight and mother's age will continue outside the range of 15 to 19 years