Merge sort

The merge-sort algorithm can be described as follows: The algorithm divides the array into two halves and applies a merge sort on each half recursively. After the two halves are sorted, the algorithm then merges them.

 

Merge sort algorithm

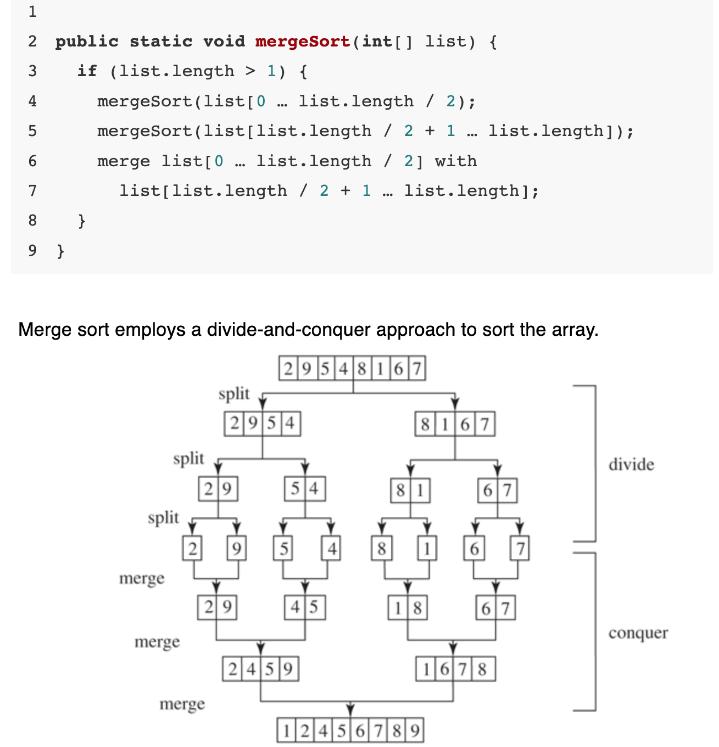
The above figure illustrates a merge sort of an array of eight elements (2 9 5 4 8 1 6 7). The original array is split into (2 9 5 4) and (8 1 6 7). Apply a merge sort on these two subarrays recursively to split (2 9 5 4) into (2 9) and (5 4) and (8 1 6 7) into (8 1) and (6 7). This process continues until the subarray contains only one element. For example, array ( 2 9) is split into the subarrays (2) and (9). Since array (2) contains a single element, it cannot be further split. Now merge (2) with (9) into a new sorted array (2 9) and (5) with (4) into a new sorted array (4 5). Merge (2 9) with (4 5) into a new sorted array (2 4 5 9) and finally merge (2 4 5 9) with (1 6 7 8) into a new sorted array (1 2 4 5 6 7 8 9).

 

Assignment

• Explain how merge sort works. What is the time complexity for a merge sort? Discuss the best-case and worst-case scenario.
• Compose a merge sort code in Java. Take few user integer inputs and apply a merge sort algorithm. Explain the code in detail.

I think I know some of the questions but I would like further explanation specifically with the code. I don't know if my answers are correct. Please help.

Explain how merge sort works: The algorithm divides the array into two halves and applies a merge sort on each half recursively. After the two halves are sorted, the algorithm then merges them.

What is the time complexity for a merge sort? Time complexity can be expressed as following recurrence relation. T(n) = 2T(n/2) + O(n). The solution of the above recurrence is O(nLogn)

Discuss the best-case and worst-case scenario: The time complexity of MergeSort is O(n*Log n) in all the 3 cases (worst, average and best) as the merge sort always divides the array into two halves and takes linear time to merge two halves.

Java code: 

public class MergeSort {
 /** The method for sorting the numbers */
 public static void mergeSort(int[] list) {
   if (list.length > 1) {
     // Merge sort the first half
     int[] firstHalf = new int[list.length / 2];
     System.arraycopy(list, 0, firstHalf, 0, list.length / 2);
     mergeSort(firstHalf);

     // Merge sort the second half
     int secondHalfLength = list.length - list.length / 2;
     int[] secondHalf = new int[secondHalfLength];
     System.arraycopy(list, list.length / 2,
       secondHalf, 0, secondHalfLength);
     mergeSort(secondHalf);

     // Merge firstHalf with secondHalf into list
     merge(firstHalf, secondHalf, list);
   }
 }

 /** Merge two sorted lists */
 public static void merge(int[] list1, int[] list2, int[] temp) {
   int current1 = 0; // Current index in list1
   int current2 = 0; // Current index in list2
   int current3 = 0; // Current index in temp

   while (current1 < list1.length && current2 < list2.length) {
     if (list1[current1] < list2[current2])
       temp[current3++] = list1[current1++];
     else
       temp[current3++] = list2[current2++];
   }

   while (current1 < list1.length)
     temp[current3++] = list1[current1++];

   while (current2 < list2.length)
     temp[current3++] = list2[current2++];
 }

 /** A test method */
 public static void main(String[] args) {
   int[] list = {2, 3, 2, 5, 6, 1, -2, 3, 14, 12};
   mergeSort(list);
   for (int i = 0; i < list.length; i++)
     System.out.print(list[i] + " ");
 }
}
 

1 2 public static void mergeSort (int[] list) { 3 if (list.length > 1) { 4 5 6 7 mergeSort (list [0 list. length / 2); mergeSort (list [list.length / 2 + 1 ... list.length]); merge list [0... list.length / 2] with list [list.length / 2 + 1 ... list.length]; 8 } 9 } Merge sort employs a divide-and-conquer approach to sort the array. 29548167 split 2954 8167 split divide 29 54 81 67 split 8 merge 29 45 18 67 conquer merge 2459 1678 merge 12456789