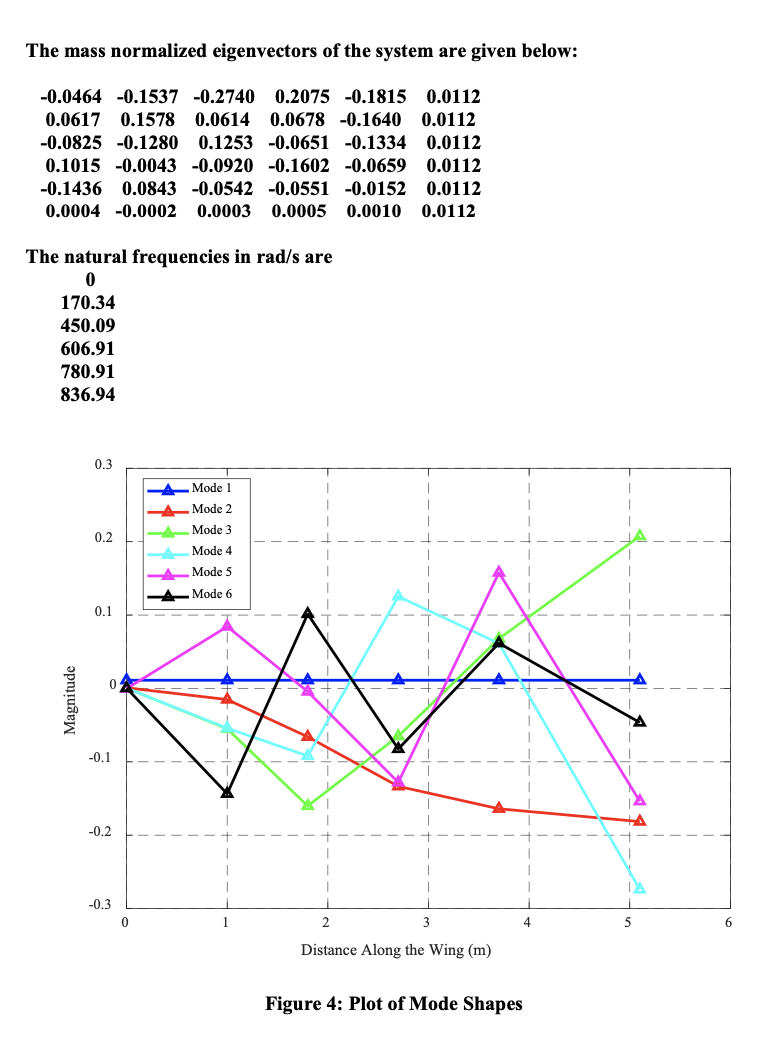
%m-file to calculate eigenvalues and eigenvectors % inertia values in kg-m^2 J1=5.65; J2=15.6; J3=16.38; J4=20.45; J5=29.38; J6 .5*15818; % stiffness values in N-m/rad K1=1.7e06; K2 3.4e06; K3=2.48e06; K4 4.07e06; K5=13.6e06; % form mass and stiffness matrices mass-diag([J1 J2 J3 J4 J5 J6]); stiff=[K1-K1 0 0 0 0; -K1 K1+K2 -K2 000;0-K2 K2+K3 -K3 0 0; ... 00-K3 K3+K4 -K4 0;000 -K4 K4+K5 -K5;0000 -K5 K5]; % find eigenvectors and eigenvalues (natural frequencies) [eigvectl eig] =eig (inv (mass) * stiff); % mass normalize eigenvectors a=eigvect1'*mass*eigvectl; for i=1:6 end for j=1:6 end eigvect (j, i) =eigvectl(j, i)/sqrt(a(i,i)); natfreq=sort (real (diag(sqrt (eig)))); distance=[0 1 1.8 2.7 3.7 5.1]; fontsize=14; fontsize=14; figure ('Name', 'Mode Shape Plots') plot (distance, flipud (eigvect (1:6,6)),'b^-', 'Linewidth', 2); hold on; plot (distance, flipud (eigvect (1:6,5)), 'r^-', 'Linewidth', 2); hold on; plot (distance, flipud (eigvect (1:6,4)),'g^-', 'Linewidth', 2); hold on; plot (distance, flipud (eigvect (1:6,3)), 'c^-', 'Linewidth', 2); hold on; plot (distance, flipud (eigvect (1:6,2)), 'm^-', 'Linewidth', 2); hold on; plot (distance, flipud (eigvect (1:6,1)), 'k^', 'Linewidth', 2); hold on; xlabel('Distance Along the Wing (m)', 'FontName', 'Times', 'FontSize', fontsize); ylabel('Magnitude', 'FontName', 'Times', 'FontSize', fontsize); legend ('Mode 1', 'Mode 2', 'Mode 3', 'Mode 4', 'Mode 5', 'Mode 6'); set (gca, 'FontName', 'Times', 'FontSize', fontsize); grid; set (gca, 'gridalpha',.8, 'gridlinestyle', '--') The mass normalized eigenvectors of the system are given below: -0.0464 -0.1537 -0.2740 0.2075 -0.1815 0.0112 0.0617 0.1578 0.0614 0.0678 -0.1640 0.0112 -0.0825 -0.1280 0.1253 -0.0651 -0.1334 0.0112 0.1015 -0.0043 -0.0920 -0.1602 -0.0659 0.0112 -0.1436 0.0843 -0.0542 -0.0551 -0.0152 0.0112 0.0004 -0.0002 0.0003 0.0005 0.0010 0.0112 The natural frequencies in rad/s are Magnitude 0 170.34 450.09 606.91 780.91 836.94 -0.1 -0.2 0.3 Mode 1 Mode 2 Mode 3 0.2 Mode 4 Mode 5 0.1 Mode 6 -0.3 2 3 Distance Along the Wing (m) Figure 4: Plot of Mode Shapes 5 6