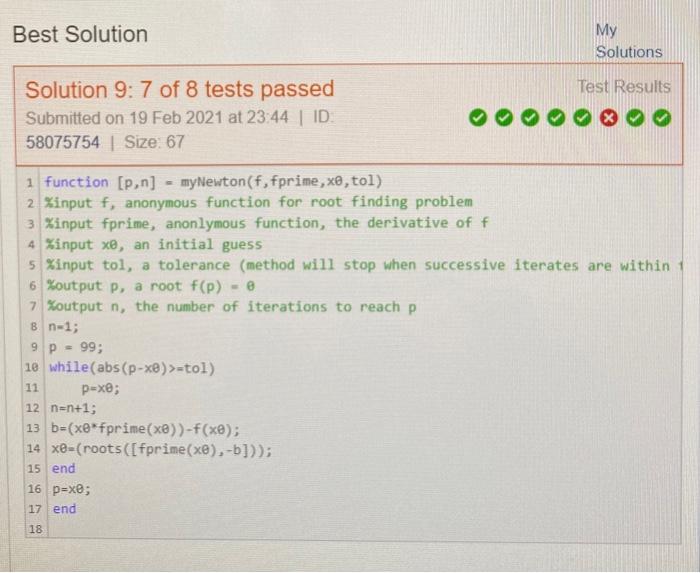
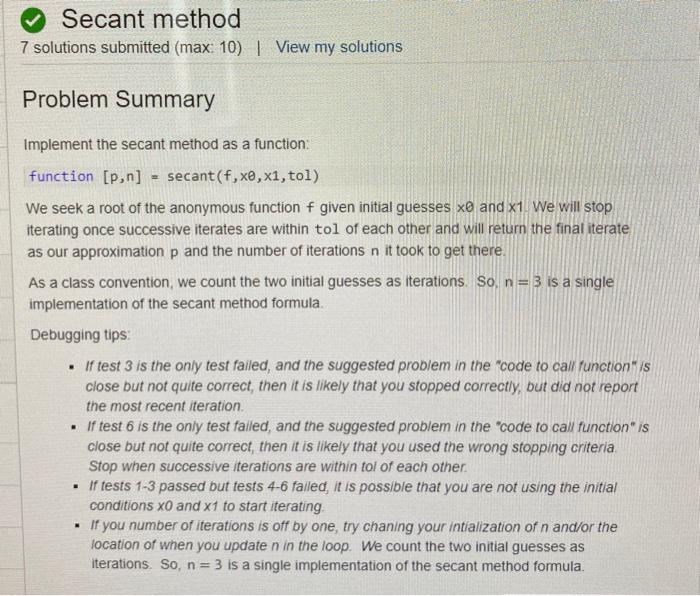
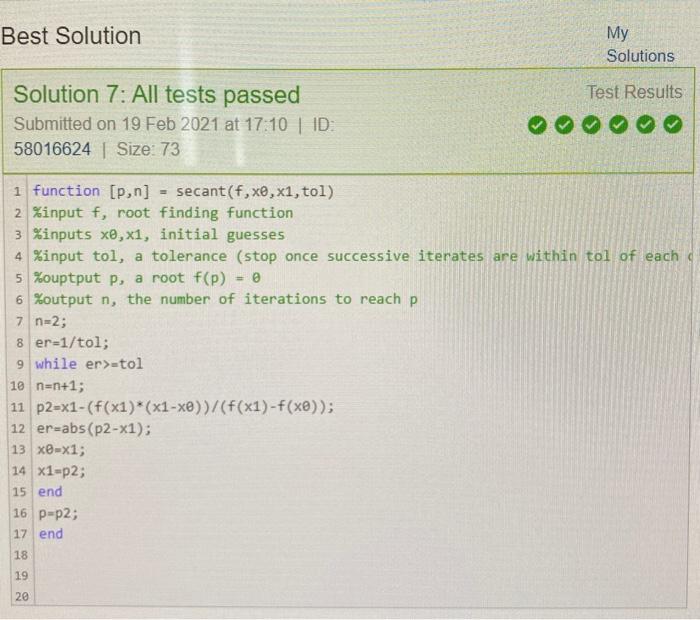
MGHW5 for info;
Bisection Method:
Newton's Method:
Secant method:
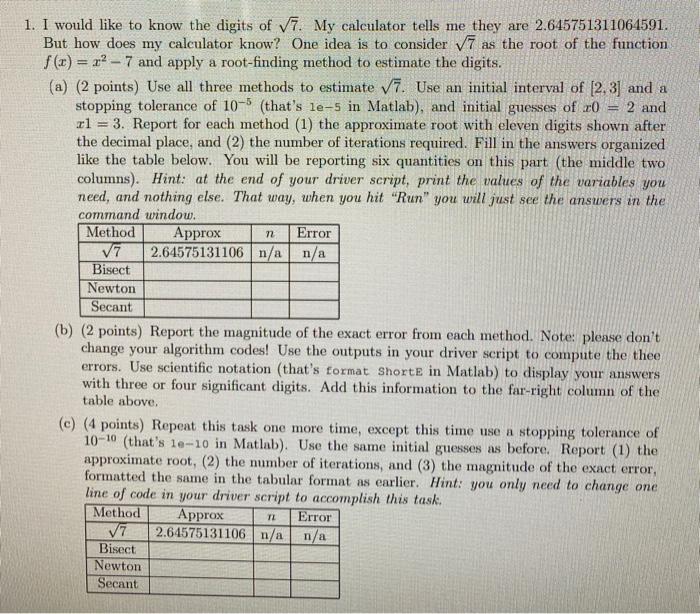
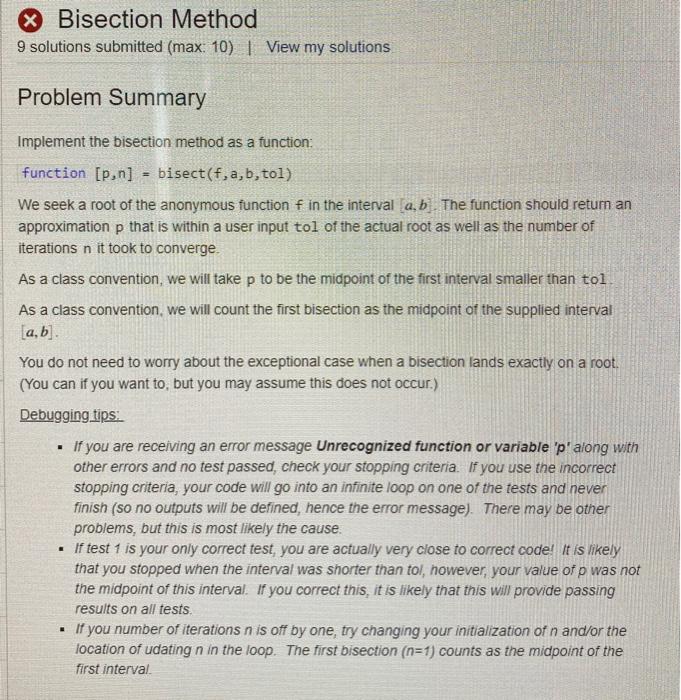
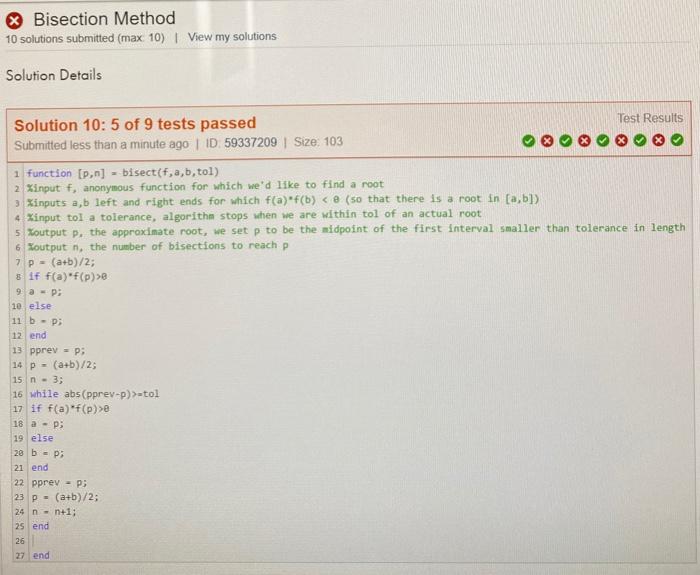
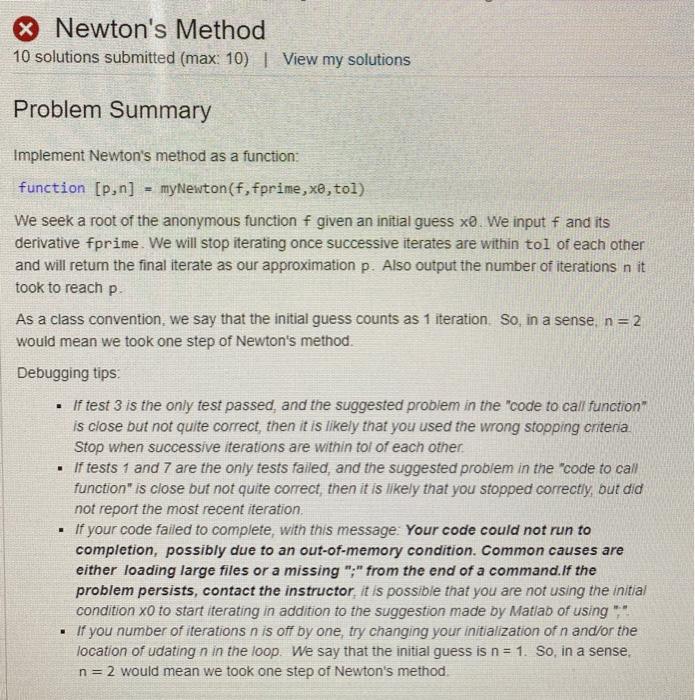
This assignment deals with root-finding algorithms and should be done using the code from MGHW5. It is recommended that you take the following steps: Download your complete and correct algorithms (bisect.m, myNewton.m, and secant.m) from MGHW5 and save it to your own computer in a folder called Root Finding. Do not change the code in any of these three files! Open a new (driver) script .m-file to complete the problems on this homework assignment. Call the functions you wrote. If you need to compute something like error (which is not an output of the algorithms), don't change the algorithms. Get the outputs and then manipulate them in your driver script. In conjunction with your driver script, refer to your handwritten notes about the algorithms to answer the "math" parts of the questions. n 1. I would like to know the digits of V7. My calculator tells me they are 2.645751311061591. But how does my calculator know? One idea is to consider V7 as the root of the function f (x)= 22 - 7 and apply a root-finding method to estimate the digits. (a) (2 points) Use all three methods to estimate Vi. Use an initial interval of (2.3) and a stopping tolerance of 10-5 (that's le-s in Matlab), and initial guesses of x0 = 2 and rl = 3. Report for each method (1) the approximate root with eleven digits shown after the decimal place, and (2) the number of iterations required. Fill in the answers organized like the table below. You will be reporting six quantities on this part (the middle two columns). Hint: at the end of your driver script, print the values of the variables you need, and nothing else. That way, when you hit "Run" you will just see the answers in the command window. Method Approx Error 77 2.64575131106 n/a n/a Bisect Newton Secant (b) (2 points) Report the magnitude of the exact error from each method. Note: please don't change your algorithm codes! Use the outputs in your driver script to compute the thee errors. Use scientific notation (that's format shorte in Matlab) to display your answers with three or four significant digits. Add this information to the far-right column of the table above (c) (4 points) Repeat this task one more time, except this time use a stopping tolerance of 10-10 (that's le-10 in Matlab). Use the same initial guesses as before. Report (1) the approximate root, (2) the number of iterations, and (3) the magnitude of the exact error, formatted the same in the tabular format as earlier. Hint: you only need to change one line of code in your driver script to accomplish this task. Method Approx Error 77 2.64575131106 n/a n/a Bisect Newton Secant TL (d) (2 points) Try this again with a stopping tolerance of 10-16. What happened? Do you have any ideas why this happened? (You will be able to fully explain what's happening after class on Wednesday 2/24, but for this problem, any reasonable conjecture will earn points. You do not need to wait for class on 2/24; in fact, it is preferred if you try to answer this before class that day!) (e) Make comments about the following observations. i. (2 points) Based on the number of iterations, rank the methods in order from fastest to slowest on this particular problem. Explain how this is consistent with our discussion about convergence rates. ii. (3 points) Comment about the stopping criteria compared to the actual error. (1) Which is larger? Do you think this will always be the case? (2) What happened to the error when we decrease the stopping criteria in parts (b) to (e)? Do you think this will always be the case? X Bisection Method 9 solutions submitted (max: 10) | View my solutions Problem Summary Implement the bisection method as a function: function [p, n] = bisect(f, a, b, tol) We seek a root of the anonymous function f in the interval a. b. The function should retum an approximation p that is within a user input tol of the actual root as well as the number of iterations n it took to converge. As a class convention, we will take p to be the midpoint of the first interval smaller than tol As a class convention, we will count the first bisection as the midpoint of the supplied interval [a,b] You do not need to worry about the exceptional case when a bisection lands exactly on a root. (You can if you want to, but you may assume this does not occur.) Debugging tips: If you are receiving an error message Unrecognized function or variable 'p' along with other errors and no test passed, check your stopping criteria. If you use the incorrect stopping criteria, your code will go into an infinite loop on one of the tests and never finish (so no outputs will be defined, hence the error message). There may be other problems, but this is most likely the cause. If test 1 is your only correct test, you are actually very close to correct code! It is likely that you stopped when the interval was shorter than tol, however, your value of p was not the midpoint of this interval. If you correct this, it is likely that this will provide passing results on all tests. If you number of iterations n is off by one, try changing your initialization of n and/or the location of udating n in the loop. The first bisection (n=1) counts as the midpoint of the first interval . X Bisection Method 10 solutions submitted (max 10) | View my solutions Solution Details Test Results Solution 10: 5 of 9 tests passed Submitted less than a minute ago ID 59337209 Size: 103 1 function (p.n] - bisect(f, a, b, tol) 2. Xinput f, anonymous function for which we'd like to find a root 3 Xinputs a,b left and right ends for which f(a) f(b) stol 17 if f(a) f(p) 18 a- 19 else 20 b = p; 21 end 22 pprev - Pi 23 - (a+b)/2; 24 n - n+1; 25 end 26 27 end X Newton's Method 10 solutions submitted (max: 10) | View my solutions Problem Summary . Implement Newton's method as a function: function [p,n] myNewton(f, fprime, x8, tol) We seek a root of the anonymous function f given an initial guess xo. We input f and its derivative fprime. We will stop iterating once successive iterates are within tol of each other and will retum the final iterate as our approximation p. Also output the number of iterations n it took to reach p As a class convention, we say that the initial guess counts as 1 iteration So, in a sense, n=2 would mean we took one step of Newton's method. Debugging tips: if test 3 is the only test passed, and the suggested problem in the "code to call function is close but not quite correct, then it is likely that you used the wrong stopping criteria. Stop when successive iterations are within tol of each other. if tests 1 and 7 are the only tests failed, and the suggested problem in the "code to call function" is close but not quite correct, then it is likely that you stopped correctly, but did not report the most recent iteration If your code failed to complete with this message. Your code could not run to completion, possibly due to an out-of-memory condition. Common causes are either loading large files or a missing ";" from the end of a command.If the problem persists, contact the instructor, it is possible that you are not using the initial condition XO to start iterating in addition to the suggestion made by Matiad of using " . If you number of iterations n is off by one, try changing your initialization of n and/or the location of udating n in the loop. We say that the initial guess is n = 1. So, in a sense n=2 would mean we took one step of Newton's method . Best Solution My Solutions Test Results Solution 9: 7 of 8 tests passed Submitted on 19 Feb 2021 at 23:44 | ID. 58075754 Size: 67 1 function [P,n] = myNewton(f,fprime ,xe,tol) 2 Sinput f, anonymous function for root finding problem 3 Xinput fprime, anonlymous function, the derivative of f 4 Xinput xe, an initial guess 5 %input tol, a tolerance (method will stop when successive iterates are within 1 6 Zoutput p, a root f(p) = 0 7 Koutput n, the number of iterations to reach p 8 n-1; 9 P = 99; 10 while(abs (P-XB)>-tol) pexe; 12 n=n+1; 13 b=(x@*fprime(x))-f(x); 14 x-(roots([fprime(x),-b])); 15 end 16 p=xe; 17 end 11 18 Secant method 7 solutions submitted (max 10) | View my solutions Problem Summary Implement the secant method as a function function [2,n] secant(f,x0, x1, tol) We seek a root of the anonymous function f given initial guesses x and x1 We will stop iterating once successive iterates are within tol of each other and will return the final iterate as our approximation p and the number of iterations n it took to get there, As a class convention, we count the two initial guesses as iterations. So, n=3 is a single implementation of the secant method formula Debugging tips: if test 3 is the only test failed, and the suggested problem in the "code to call function is close but not quite correct, then it is likely that you stopped correctly, but did not report the most recent iteration . If test 6 is the only test falled, and the suggested problem in the "code to call function" is close but not quite correct, then it is likely that you used the wrong stopping criteria Stop when successive iterations are within tol of each other If tests 1-3 passed but tests 4-6 failed, it is possible that you are not using the initial conditions x0 and x1 to start iterating If you number of iterations is off by one, try chaning your intialization of n and/or the location of when you update n in the loop. We count the two initial guesses as iterations. So, n= 3 is a single implementation of the secant method formula. Best Solution My Solutions Test Results Solution 7: All tests passed Submitted on 19 Feb 2021 at 17:10 | ID: 58016624 | Size: 73 1 function [2,n] secant(f,xe, x1, tol) 2 %input f, root finding function 3 %inputs x0, x1, initial guesses 4 %input tol, a tolerance (stop once successive iterates are within tol of each 5 %ouptput p, a root f(p) = 0 6 %output n, the number of iterations to reach p 7 n=2; 8 er=1/tol; 9 while er>=tol 10 n=n+1; 11 p2=x1-(f(x1)*(x1-x2))/(f(x1)-f(x0)); 12 er-abs (p2-x1); 13 xemx1; 14 x1=p2; 15 end 16 p=p2; 17 end 18 19 2e This assignment deals with root-finding algorithms and should be done using the code from MGHW5. It is recommended that you take the following steps: Download your complete and correct algorithms (bisect.m, myNewton.m, and secant.m) from MGHW5 and save it to your own computer in a folder called Root Finding. Do not change the code in any of these three files! Open a new (driver) script .m-file to complete the problems on this homework assignment. Call the functions you wrote. If you need to compute something like error (which is not an output of the algorithms), don't change the algorithms. Get the outputs and then manipulate them in your driver script. In conjunction with your driver script, refer to your handwritten notes about the algorithms to answer the "math" parts of the questions. n 1. I would like to know the digits of V7. My calculator tells me they are 2.645751311061591. But how does my calculator know? One idea is to consider V7 as the root of the function f (x)= 22 - 7 and apply a root-finding method to estimate the digits. (a) (2 points) Use all three methods to estimate Vi. Use an initial interval of (2.3) and a stopping tolerance of 10-5 (that's le-s in Matlab), and initial guesses of x0 = 2 and rl = 3. Report for each method (1) the approximate root with eleven digits shown after the decimal place, and (2) the number of iterations required. Fill in the answers organized like the table below. You will be reporting six quantities on this part (the middle two columns). Hint: at the end of your driver script, print the values of the variables you need, and nothing else. That way, when you hit "Run" you will just see the answers in the command window. Method Approx Error 77 2.64575131106 n/a n/a Bisect Newton Secant (b) (2 points) Report the magnitude of the exact error from each method. Note: please don't change your algorithm codes! Use the outputs in your driver script to compute the thee errors. Use scientific notation (that's format shorte in Matlab) to display your answers with three or four significant digits. Add this information to the far-right column of the table above (c) (4 points) Repeat this task one more time, except this time use a stopping tolerance of 10-10 (that's le-10 in Matlab). Use the same initial guesses as before. Report (1) the approximate root, (2) the number of iterations, and (3) the magnitude of the exact error, formatted the same in the tabular format as earlier. Hint: you only need to change one line of code in your driver script to accomplish this task. Method Approx Error 77 2.64575131106 n/a n/a Bisect Newton Secant TL (d) (2 points) Try this again with a stopping tolerance of 10-16. What happened? Do you have any ideas why this happened? (You will be able to fully explain what's happening after class on Wednesday 2/24, but for this problem, any reasonable conjecture will earn points. You do not need to wait for class on 2/24; in fact, it is preferred if you try to answer this before class that day!) (e) Make comments about the following observations. i. (2 points) Based on the number of iterations, rank the methods in order from fastest to slowest on this particular problem. Explain how this is consistent with our discussion about convergence rates. ii. (3 points) Comment about the stopping criteria compared to the actual error. (1) Which is larger? Do you think this will always be the case? (2) What happened to the error when we decrease the stopping criteria in parts (b) to (e)? Do you think this will always be the case? X Bisection Method 9 solutions submitted (max: 10) | View my solutions Problem Summary Implement the bisection method as a function: function [p, n] = bisect(f, a, b, tol) We seek a root of the anonymous function f in the interval a. b. The function should retum an approximation p that is within a user input tol of the actual root as well as the number of iterations n it took to converge. As a class convention, we will take p to be the midpoint of the first interval smaller than tol As a class convention, we will count the first bisection as the midpoint of the supplied interval [a,b] You do not need to worry about the exceptional case when a bisection lands exactly on a root. (You can if you want to, but you may assume this does not occur.) Debugging tips: If you are receiving an error message Unrecognized function or variable 'p' along with other errors and no test passed, check your stopping criteria. If you use the incorrect stopping criteria, your code will go into an infinite loop on one of the tests and never finish (so no outputs will be defined, hence the error message). There may be other problems, but this is most likely the cause. If test 1 is your only correct test, you are actually very close to correct code! It is likely that you stopped when the interval was shorter than tol, however, your value of p was not the midpoint of this interval. If you correct this, it is likely that this will provide passing results on all tests. If you number of iterations n is off by one, try changing your initialization of n and/or the location of udating n in the loop. The first bisection (n=1) counts as the midpoint of the first interval . X Bisection Method 10 solutions submitted (max 10) | View my solutions Solution Details Test Results Solution 10: 5 of 9 tests passed Submitted less than a minute ago ID 59337209 Size: 103 1 function (p.n] - bisect(f, a, b, tol) 2. Xinput f, anonymous function for which we'd like to find a root 3 Xinputs a,b left and right ends for which f(a) f(b) stol 17 if f(a) f(p) 18 a- 19 else 20 b = p; 21 end 22 pprev - Pi 23 - (a+b)/2; 24 n - n+1; 25 end 26 27 end X Newton's Method 10 solutions submitted (max: 10) | View my solutions Problem Summary . Implement Newton's method as a function: function [p,n] myNewton(f, fprime, x8, tol) We seek a root of the anonymous function f given an initial guess xo. We input f and its derivative fprime. We will stop iterating once successive iterates are within tol of each other and will retum the final iterate as our approximation p. Also output the number of iterations n it took to reach p As a class convention, we say that the initial guess counts as 1 iteration So, in a sense, n=2 would mean we took one step of Newton's method. Debugging tips: if test 3 is the only test passed, and the suggested problem in the "code to call function is close but not quite correct, then it is likely that you used the wrong stopping criteria. Stop when successive iterations are within tol of each other. if tests 1 and 7 are the only tests failed, and the suggested problem in the "code to call function" is close but not quite correct, then it is likely that you stopped correctly, but did not report the most recent iteration If your code failed to complete with this message. Your code could not run to completion, possibly due to an out-of-memory condition. Common causes are either loading large files or a missing ";" from the end of a command.If the problem persists, contact the instructor, it is possible that you are not using the initial condition XO to start iterating in addition to the suggestion made by Matiad of using " . If you number of iterations n is off by one, try changing your initialization of n and/or the location of udating n in the loop. We say that the initial guess is n = 1. So, in a sense n=2 would mean we took one step of Newton's method . Best Solution My Solutions Test Results Solution 9: 7 of 8 tests passed Submitted on 19 Feb 2021 at 23:44 | ID. 58075754 Size: 67 1 function [P,n] = myNewton(f,fprime ,xe,tol) 2 Sinput f, anonymous function for root finding problem 3 Xinput fprime, anonlymous function, the derivative of f 4 Xinput xe, an initial guess 5 %input tol, a tolerance (method will stop when successive iterates are within 1 6 Zoutput p, a root f(p) = 0 7 Koutput n, the number of iterations to reach p 8 n-1; 9 P = 99; 10 while(abs (P-XB)>-tol) pexe; 12 n=n+1; 13 b=(x@*fprime(x))-f(x); 14 x-(roots([fprime(x),-b])); 15 end 16 p=xe; 17 end 11 18 Secant method 7 solutions submitted (max 10) | View my solutions Problem Summary Implement the secant method as a function function [2,n] secant(f,x0, x1, tol) We seek a root of the anonymous function f given initial guesses x and x1 We will stop iterating once successive iterates are within tol of each other and will return the final iterate as our approximation p and the number of iterations n it took to get there, As a class convention, we count the two initial guesses as iterations. So, n=3 is a single implementation of the secant method formula Debugging tips: if test 3 is the only test failed, and the suggested problem in the "code to call function is close but not quite correct, then it is likely that you stopped correctly, but did not report the most recent iteration . If test 6 is the only test falled, and the suggested problem in the "code to call function" is close but not quite correct, then it is likely that you used the wrong stopping criteria Stop when successive iterations are within tol of each other If tests 1-3 passed but tests 4-6 failed, it is possible that you are not using the initial conditions x0 and x1 to start iterating If you number of iterations is off by one, try chaning your intialization of n and/or the location of when you update n in the loop. We count the two initial guesses as iterations. So, n= 3 is a single implementation of the secant method formula. Best Solution My Solutions Test Results Solution 7: All tests passed Submitted on 19 Feb 2021 at 17:10 | ID: 58016624 | Size: 73 1 function [2,n] secant(f,xe, x1, tol) 2 %input f, root finding function 3 %inputs x0, x1, initial guesses 4 %input tol, a tolerance (stop once successive iterates are within tol of each 5 %ouptput p, a root f(p) = 0 6 %output n, the number of iterations to reach p 7 n=2; 8 er=1/tol; 9 while er>=tol 10 n=n+1; 11 p2=x1-(f(x1)*(x1-x2))/(f(x1)-f(x0)); 12 er-abs (p2-x1); 13 xemx1; 14 x1=p2; 15 end 16 p=p2; 17 end 18 19 2e