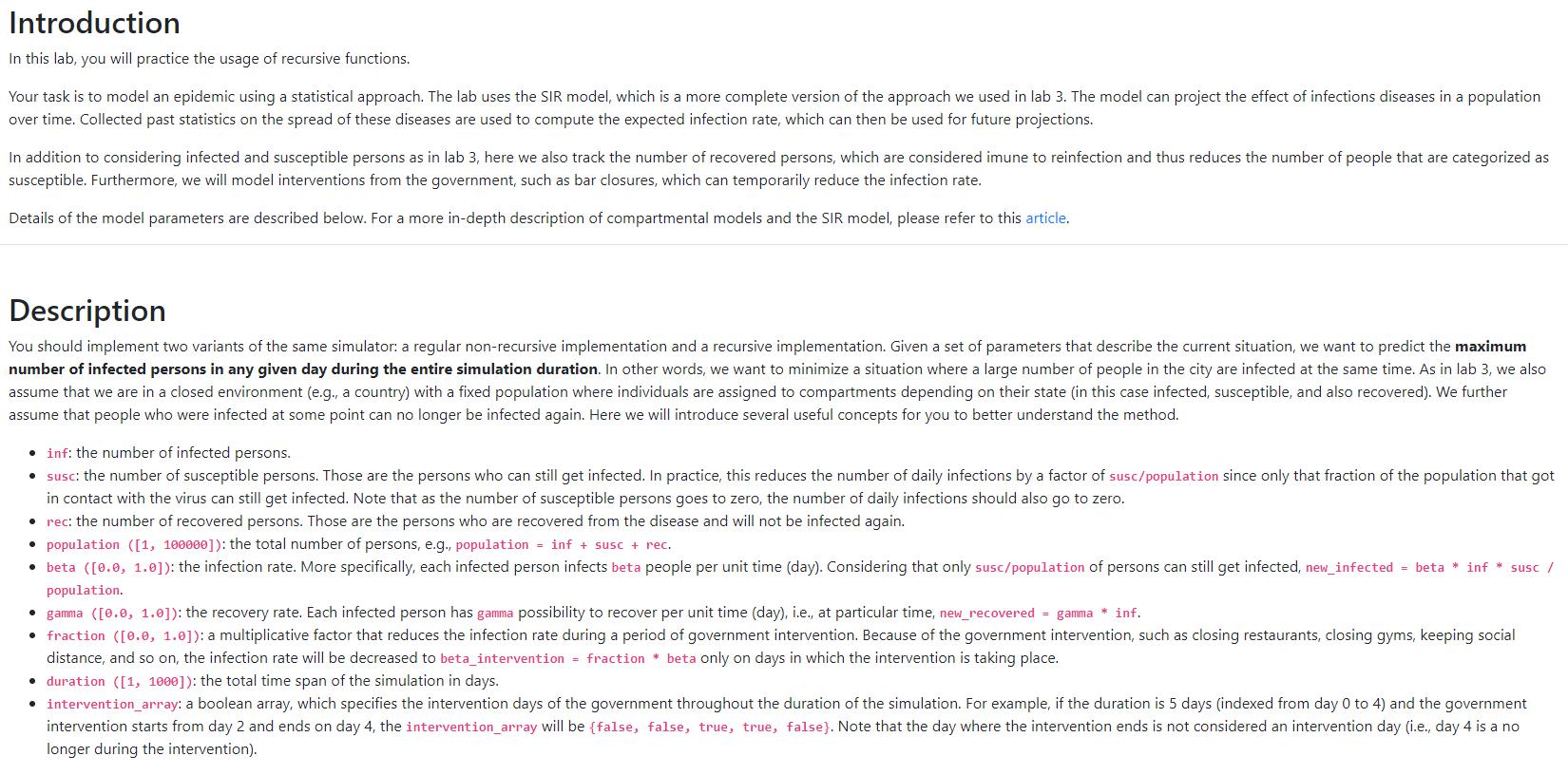
Model an epidemic using a statistical approach (recursive functions) The Skeleton code is as follows:

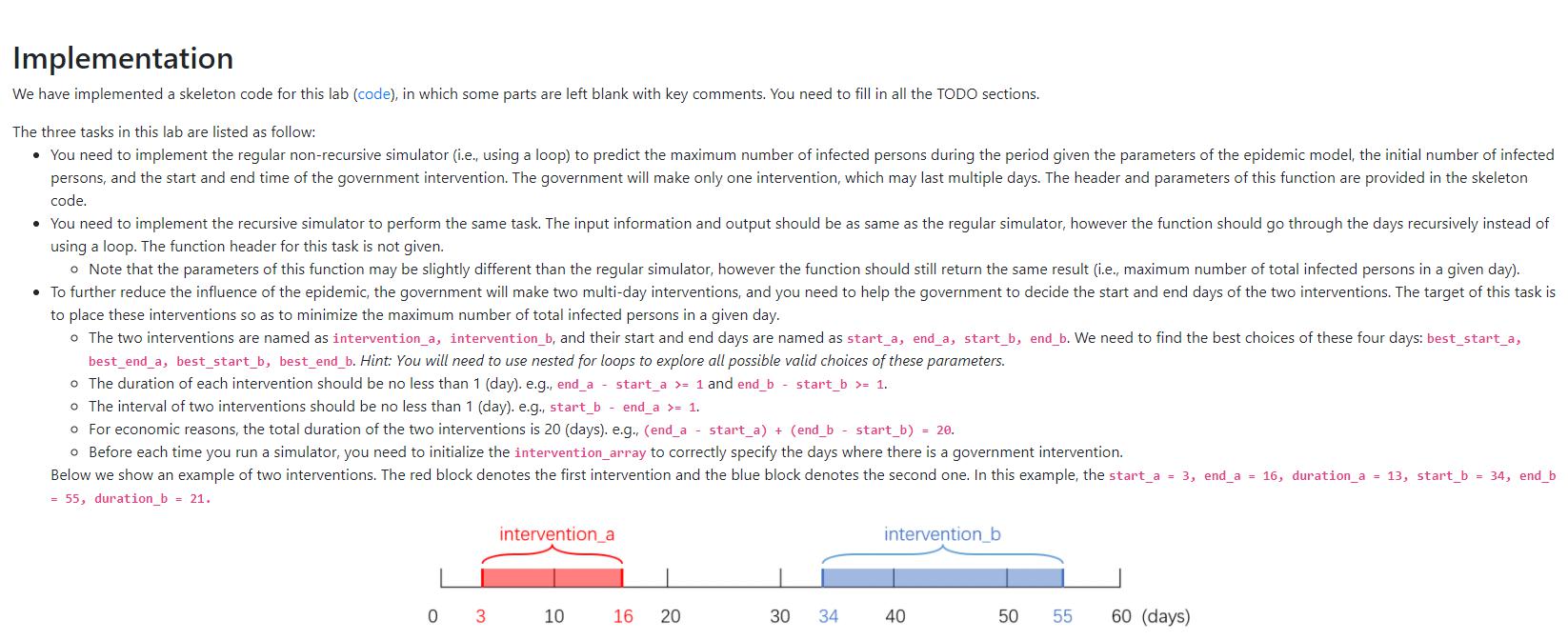
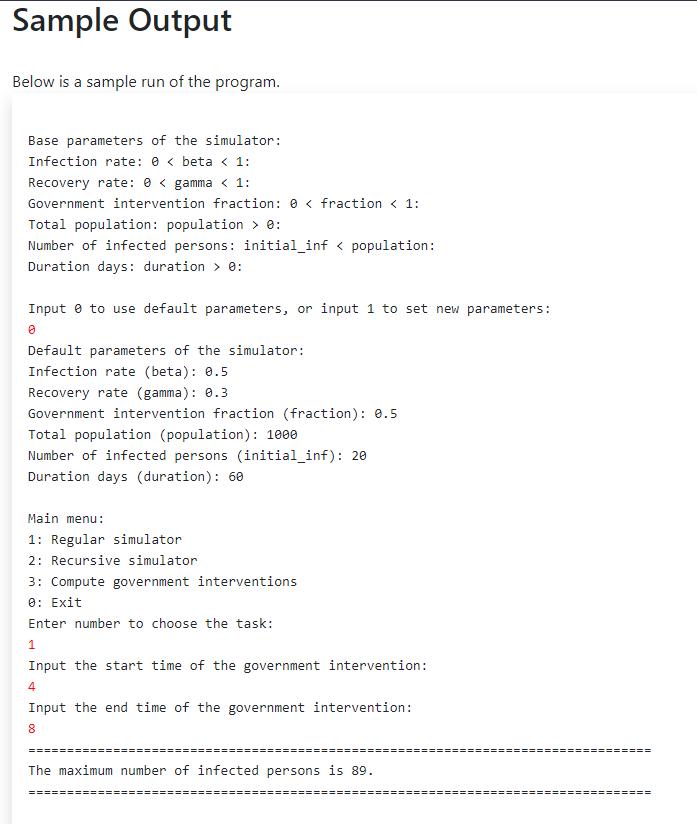
#include #include using namespace std; int regular_simulator(float beta, float gamma, float fraction, bool intervention_array[], int init_inf, int population, int duration) { /** * \param beta: infection rate * \param gamma: recovery rate * \param fraction: government intervention rate, the infection rate after intervention * should be original infection rate times fraction * \param intervention_array: boolean array, records the intervention days in the whole disease duration * \param init_inf: initial number of infected persons at beginning * \param population: total number of people * \param duration: the total time span of the simulation in days * eturn return the maximum number of the infected persons in the disease duration * **/ int inf = init_inf; int susc = population - init_inf; int rec = 0; int max_inf = init_inf; for (int t = 0; t  max_inf) max_inf = inf; } return max_inf; } // TODO 2: Implement the recursive simulator from scratch. // DO NOT use the for loop in this function. // The return value should be as same as the regular simulator, but the parameters can be different. // End of TODO 2. // Initialize the intervention array. The true means that the government intervened on that day. // Hint: Maybe it is not suitable for more than one intervention. void initialize_intervention_array(bool intervention[], int start_time, int end_time, int duration){ for (int t = 0; t = start_time && t  0: "  0: " > default_flag; if (default_flag == 1){ cout > beta; cout > gamma; cout > fraction; cout > population; cout > initial_inf; cout > duration; } else{ cout > mode; while(mode != 0 && mode != 1 && mode != 2 && mode != 3){ cout > mode; } if (mode == 1 || mode == 2){ int intervention_start_time, intervention_end_time; cout > intervention_start_time; cout > intervention_end_time; initialize_intervention_array(intervention_array, intervention_start_time, intervention_end_time, duration); if (mode == 1) { // TODO 1 max_inf = regular_simulator(beta, gamma, fraction, intervention_array, initial_inf, population, duration); // End of TODO 1 cout  20. // 3. Use the regular_simulator or recursive_simulator to find the maximum number of total infected persons. int max_intervention_duration = 20; int best_start_a = 0; int best_end_a = 0; int best_start_b = 0; int best_end_b = 0; int max_infected = 9999999; // Implement TODO 3 here. cout   Introduction In this lab, you will practice the usage of recursive functions. Your task is to model an epidemic using a statistical approach. The lab uses the SIR model, which is a more complete version of the approach we used in lab 3. The model can project the effect of infections diseases in a population over time. Collected past statistics on the spread of these diseases are used to compute the expected infection rate, which can then be used for future projections. In addition to considering infected and susceptible persons as in lab 3, here we also track the number of recovered persons, which are considered imune to reinfection and thus reduces the number of people that are categorized as susceptible. Furthermore, we will model interventions from the government, such as bar closures, which can temporarily reduce the infection rate. Details of the model parameters are described below. For a more in-depth description of compartmental models and the SIR model, please refer to this article. Description You should implement two variants of the same simulator: a regular non-recursive implementation and a recursive implementation. Given a set of parameters that describe the current situation, we want to predict the maximum number of infected persons in any given day during the entire simulation duration. In other words, we want to minimize a situation where a large number of people in the city are infected at the same time. As in lab 3, we also assume that we are in a closed environment (e.g., a country) with a fixed population where individuals are assigned to compartments depending on their state (in this case infected, susceptible, and also recovered). We further assume that people who were infected at some point can no longer be infected again. Here we will introduce several useful concepts for you to better understand the method. . inf: the number of infected persons.  susc: the number of susceptible persons. Those are the persons who can still get infected. In practice, this reduces the number of daily infections by a factor of susc/population since only that fraction of the population that got in contact with the virus can still get infected. Note that as the number of susceptible persons goes to zero, the number of daily infections should also go to zero.  rec: the number of recovered persons. Those are the persons who are recovered from the disease and will not be infected again.  population ([1, 100000]): the total number of persons, e.g., population - inf + susc + rec.  beta ([0.0, 1.0]): the infection rate. More specifically, each infected person infects beta people per unit time (day). Considering that only susc/population of persons can still get infected, new_infected = beta * inf * susc / population.  gamma ([0.0, 1.0]): the recovery rate. Each infected person has gamma possibility to recover per unit time (day), i.e., at particular time, new_recovered = gamma * inf.  fraction ([0.0, 1.0]): a multiplicative factor that reduces the infection rate during a period of government intervention. Because of the government intervention, such as closing restaurants, closing gyms, keeping social distance, and so on, the infection rate will be decreased to beta_intervention = fraction * beta only on days in which the intervention is taking place.  duration ([1, 1900]): the total time span of the simulation in days.  intervention_array: a boolean array, which specifies the intervention days of the government throughout the duration of the simulation. For example, if the duration is 5 days (indexed from day 0 to 4) and the government intervention starts from day 2 and ends on day 4, the intervention_array will be {false, false, true, true, false}. Note that the day where the intervention ends is not considered an intervention day (i.e., day 4 is a no longer during the intervention). Implementation We have implemented a skeleton code for this lab (code), in which some parts are left blank with key comments. You need to fill in all the TODO sections. The three tasks in this lab are listed as follow:  You need to implement the regular non-recursive simulator (i.e., using a loop) to predict the maximum number of infected persons during the period given the parameters of the epidemic model, the initial number of infected persons, and the start and end time of the government intervention. The government will make only one intervention, which may last multiple days. The header and parameters of this function are provided in the skeleton code.  You need to implement the recursive simulator to perform the same task. The input information and output should be as same as the regular simulator, however the function should go through the days recursively instead of using a loop. The function header for this task is not given. o Note that the parameters of this function may be slightly different than the regular simulator, however the function should still return the same result (i.e., maximum number of total infected persons in a given day).  To further reduce the influence of the epidemic, the government will make two multi-day interventions, and you need to help the government to decide the start and end days of the two interventions. The target of this task is to place these interventions so as to minimize the maximum number of total infected persons in a given day. The two interventions are named as intervention a, intervention_b, and their start and end days are named as start_a, end_a, start_b, end_b. We need to find the best choices of these four days: best_start_a, best_end_a, best_start_b, best_end_b. Hint: You will need to use nested for loops to explore all possible valid choices of these parameters. The duration of each intervention should be no less than 1 (day). e.g., end_a - start_a >= 1 and end_b - start_b >= 1. o The interval of two interventions should be no less than 1 (day). e.g., start_b - end_a >- 1. o For economic reasons, the total duration of the two interventions is 20 (days). e.g., (end_a - start_a) + (end_b - start_b) = 20. o Before each time you run a simulator, you need to initialize the intervention_array to correctly specify the days where there is a government intervention. Below we show an example of two interventions. The red block denotes the first intervention and the blue block denotes the second one. In this example, the start_a = 3, end_a = 16, duration_a = 13, start_b = 34, end_b = 55, duration_b = 21. intervention a intervention b 0 3 10 16 20 30 34 40 50 55 60 days) Sample Output Below is a sample run of the program. Base parameters of the simulator: Infection rate: @  e: Number of infected persons: initial_inf  0: Input o to use default parameters, or input 1 to set new parameters: Default parameters of the simulator: Infection rate (beta): 0.5 Recovery rate (gamma): 0.3 Government intervention fraction (fraction): 0.5 Total population (population): 1000 Number of infected persons (initial_inf): 20 Duration days (duration): 60 Main menu: 1: Regular simulator 2: Recursive simulator 3: Compute government interventions 0: Exit Enter number to choose the task: 1 Input the start time of the government intervention: 4 Input the end time of the government intervention: 8 The maximum number of infected persons is 89. == Main menu: 1: Regular simulator 2: Recursive simulator 3: Compute government interventions 0: Exit Enter number to choose the task: 2 Input the start time of the government intervention: 5 Input the end time of the government intervention: 15 === The maximum number of infected persons is 59. Main menu: 1: Regular simulator 2: Recursive simulator 3: Compute government interventions 0 : Exit Enter number to choose the task: 3 best_start_a: 2 best_end_a: 11 best_start_b: 17 best_end_b: 28 max_infected: 35 If the first government intervention ranges from 2 to 11, second intervention ranges from 17 to 28, we can reduce the maximum of total infected persons to 35. ===== Main menu: 1: Regular simulator 2: Recursive simulator 3: Compute government interventions 0: Exit Enter number to choose the task: Exit.  Introduction In this lab, you will practice the usage of recursive functions. Your task is to model an epidemic using a statistical approach. The lab uses the SIR model, which is a more complete version of the approach we used in lab 3. The model can project the effect of infections diseases in a population over time. Collected past statistics on the spread of these diseases are used to compute the expected infection rate, which can then be used for future projections. In addition to considering infected and susceptible persons as in lab 3, here we also track the number of recovered persons, which are considered imune to reinfection and thus reduces the number of people that are categorized as susceptible. Furthermore, we will model interventions from the government, such as bar closures, which can temporarily reduce the infection rate. Details of the model parameters are described below. For a more in-depth description of compartmental models and the SIR model, please refer to this article. Description You should implement two variants of the same simulator: a regular non-recursive implementation and a recursive implementation. Given a set of parameters that describe the current situation, we want to predict the maximum number of infected persons in any given day during the entire simulation duration. In other words, we want to minimize a situation where a large number of people in the city are infected at the same time. As in lab 3, we also assume that we are in a closed environment (e.g., a country) with a fixed population where individuals are assigned to compartments depending on their state (in this case infected, susceptible, and also recovered). We further assume that people who were infected at some point can no longer be infected again. Here we will introduce several useful concepts for you to better understand the method. . inf: the number of infected persons.  susc: the number of susceptible persons. Those are the persons who can still get infected. In practice, this reduces the number of daily infections by a factor of susc/population since only that fraction of the population that got in contact with the virus can still get infected. Note that as the number of susceptible persons goes to zero, the number of daily infections should also go to zero.  rec: the number of recovered persons. Those are the persons who are recovered from the disease and will not be infected again.  population ([1, 100000]): the total number of persons, e.g., population - inf + susc + rec.  beta ([0.0, 1.0]): the infection rate. More specifically, each infected person infects beta people per unit time (day). Considering that only susc/population of persons can still get infected, new_infected = beta * inf * susc / population.  gamma ([0.0, 1.0]): the recovery rate. Each infected person has gamma possibility to recover per unit time (day), i.e., at particular time, new_recovered = gamma * inf.  fraction ([0.0, 1.0]): a multiplicative factor that reduces the infection rate during a period of government intervention. Because of the government intervention, such as closing restaurants, closing gyms, keeping social distance, and so on, the infection rate will be decreased to beta_intervention = fraction * beta only on days in which the intervention is taking place.  duration ([1, 1900]): the total time span of the simulation in days.  intervention_array: a boolean array, which specifies the intervention days of the government throughout the duration of the simulation. For example, if the duration is 5 days (indexed from day 0 to 4) and the government intervention starts from day 2 and ends on day 4, the intervention_array will be {false, false, true, true, false}. Note that the day where the intervention ends is not considered an intervention day (i.e., day 4 is a no longer during the intervention). Implementation We have implemented a skeleton code for this lab (code), in which some parts are left blank with key comments. You need to fill in all the TODO sections. The three tasks in this lab are listed as follow:  You need to implement the regular non-recursive simulator (i.e., using a loop) to predict the maximum number of infected persons during the period given the parameters of the epidemic model, the initial number of infected persons, and the start and end time of the government intervention. The government will make only one intervention, which may last multiple days. The header and parameters of this function are provided in the skeleton code.  You need to implement the recursive simulator to perform the same task. The input information and output should be as same as the regular simulator, however the function should go through the days recursively instead of using a loop. The function header for this task is not given. o Note that the parameters of this function may be slightly different than the regular simulator, however the function should still return the same result (i.e., maximum number of total infected persons in a given day).  To further reduce the influence of the epidemic, the government will make two multi-day interventions, and you need to help the government to decide the start and end days of the two interventions. The target of this task is to place these interventions so as to minimize the maximum number of total infected persons in a given day. The two interventions are named as intervention a, intervention_b, and their start and end days are named as start_a, end_a, start_b, end_b. We need to find the best choices of these four days: best_start_a, best_end_a, best_start_b, best_end_b. Hint: You will need to use nested for loops to explore all possible valid choices of these parameters. The duration of each intervention should be no less than 1 (day). e.g., end_a - start_a >= 1 and end_b - start_b >= 1. o The interval of two interventions should be no less than 1 (day). e.g., start_b - end_a >- 1. o For economic reasons, the total duration of the two interventions is 20 (days). e.g., (end_a - start_a) + (end_b - start_b) = 20. o Before each time you run a simulator, you need to initialize the intervention_array to correctly specify the days where there is a government intervention. Below we show an example of two interventions. The red block denotes the first intervention and the blue block denotes the second one. In this example, the start_a = 3, end_a = 16, duration_a = 13, start_b = 34, end_b = 55, duration_b = 21. intervention a intervention b 0 3 10 16 20 30 34 40 50 55 60 days) Sample Output Below is a sample run of the program. Base parameters of the simulator: Infection rate: @  e: Number of infected persons: initial_inf  0: Input o to use default parameters, or input 1 to set new parameters: Default parameters of the simulator: Infection rate (beta): 0.5 Recovery rate (gamma): 0.3 Government intervention fraction (fraction): 0.5 Total population (population): 1000 Number of infected persons (initial_inf): 20 Duration days (duration): 60 Main menu: 1: Regular simulator 2: Recursive simulator 3: Compute government interventions 0: Exit Enter number to choose the task: 1 Input the start time of the government intervention: 4 Input the end time of the government intervention: 8 The maximum number of infected persons is 89. == Main menu: 1: Regular simulator 2: Recursive simulator 3: Compute government interventions 0: Exit Enter number to choose the task: 2 Input the start time of the government intervention: 5 Input the end time of the government intervention: 15 === The maximum number of infected persons is 59. Main menu: 1: Regular simulator 2: Recursive simulator 3: Compute government interventions 0 : Exit Enter number to choose the task: 3 best_start_a: 2 best_end_a: 11 best_start_b: 17 best_end_b: 28 max_infected: 35 If the first government intervention ranges from 2 to 11, second intervention ranges from 17 to 28, we can reduce the maximum of total infected persons to 35. ===== Main menu: 1: Regular simulator 2: Recursive simulator 3: Compute government interventions 0: Exit Enter number to choose the task: Exit