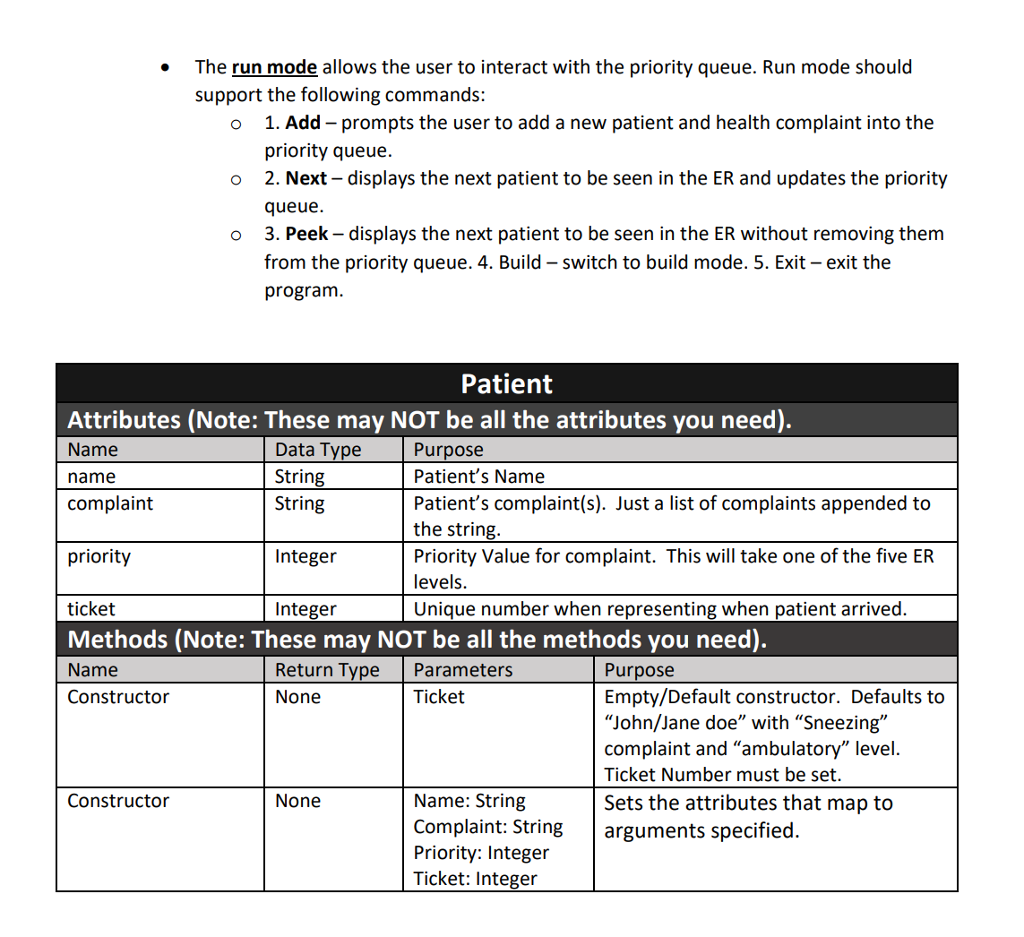
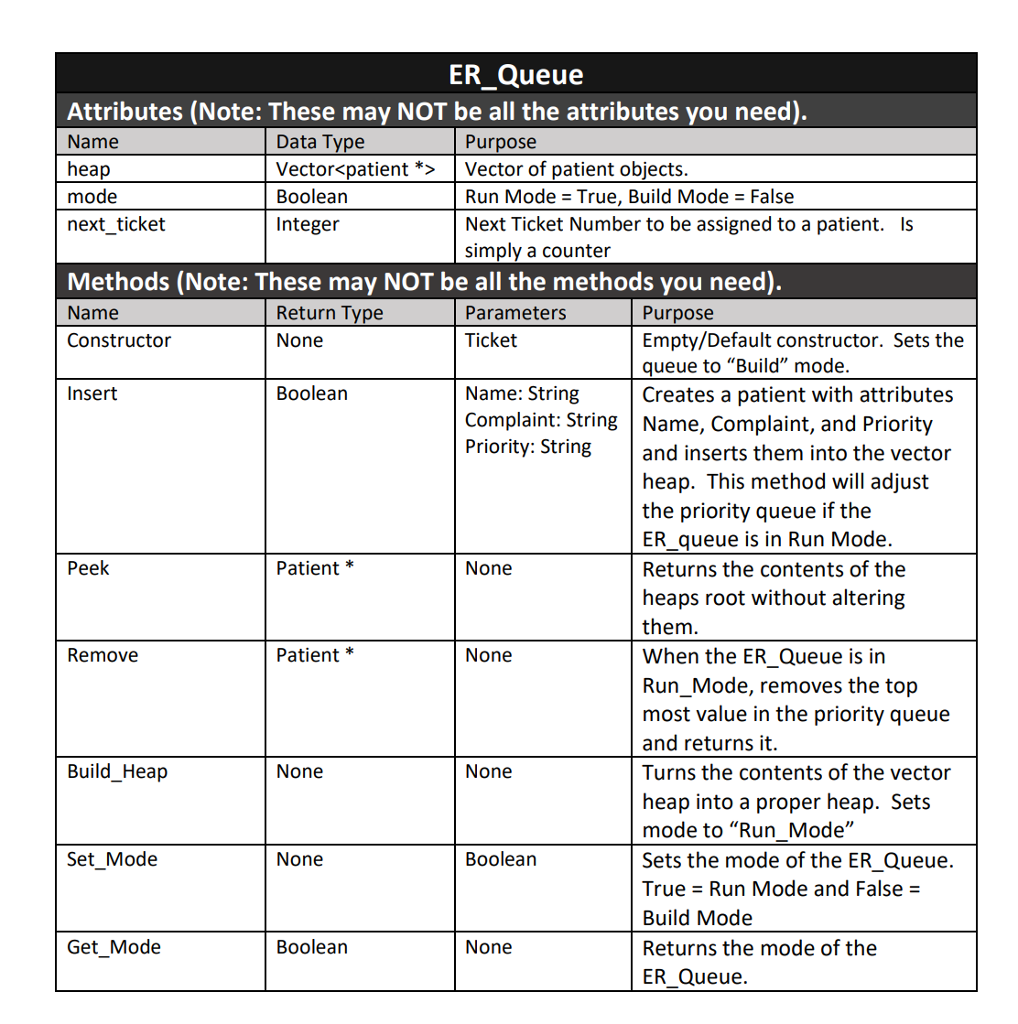
Must be in C++. Use the following as a base for program.

heap.h-

#pragma once #include  using std::vector; #define MODE_MAX true #define MODE_MIN false template  class Heap { public: vector heap; bool mode; Heap() { heap.push_back((T)nullptr); //This heap will have a root //based at element 1 this->mode = MODE_MIN; } Heap(bool mode) { //"This" is equivelant to "self" in pyhon. //It is a pointer to the object that calls the function. this->mode = mode; heap.push_back((T)nullptr); //This heap will have a root //based at element 1 } void Insert(T data) { heap.push_back(data); if (mode == MODE_MIN) bubble_up_min(); else bubble_up_max(); } T Remove() { //Copy the root into a temporary variable. T tmp = heap[1]; //Move the back node to the front of the heap. T lastElement = heap[heap.size() - 1]; heap[1] = lastElement; heap.pop_back(); //Bubble Down the root. if (mode == MODE_MIN) { bubble_down_min(1); } else bubble_down_max(1); return tmp; } bool isEmpty() { return (heap.size()  1) { //Bubble up as long as the child is smaller than the parent. if (heap[i]  1) { //Bubble up as long as the child is smaller than the parent. if (heap[i] > heap[p]) { swap(i, p); i = p; p = i / 2; } else i = -1; } } void bubble_down_min(int startIndex) { int node = startIndex; bool cont = true; while (cont) { int leftChild = 2 * node; int rightChild = 2 * node + 1; bool isNode = (node = left AND right. heap property fixed. cont = false; } else if (isNode && isLeft)//Only Has a left { //Swap based on which child is smaller. if (heap[leftChild]  heap[rightChild]) { swap(node, leftChild); node = leftChild; } else { swap(node, rightChild); node = rightChild; } } //left > node > right else if (heap[leftChild] > heap[node] && heap[node] > heap[rightChild]) { //Swap with right swap(node, rightChild); node = rightChild; } //right > node > left else if (heap[rightChild] > heap[node] && heap[node] > heap[leftChild]) { //Swap with left swap(node, leftChild); node = leftChild; } else if (heap[node] > heap[leftChild] && heap[node] == heap[rightChild]) { swap(node, leftChild); node = leftChild; } else if (heap[node] == heap[leftChild] && heap[node] > heap[rightChild]) { swap(node, rightChild); node = rightChild; } else /ode >= left AND right. heap property fixed. { cont = false; } } else if (isNode && isLeft)//Only Has a left { //Swap based on which child is larger. if (heap[leftChild] > heap[node]) { swap(node, leftChild); node = leftChild; //We know there's no more nodes to swap at this point. //Any node with only a left child has a left child that //is the last node in the heap. Stop. } else { cont = false; } } else//Either the parent is a leaf node or it doesn't exist. { cont = false; } } } };

main.cpp:

#include"Heap.h" #include using std::cout; using std::endl; int main() { Heap h(MODE_MAX); h.Insert(42); h.Insert(15); h.Insert(4); h.Insert(3); h.Insert(20); h.Insert(2); h.Insert(12); h.Insert(11); h.Insert(3); h.Insert(6); h.Insert(1); while (!h.isEmpty()) { cout   Background Queuing is a problem which is commonly encountered in stores, movie theaters, IT services, and hospitals; many people or problems waiting in line to be addressed in an orderly and controlled fashion. Basic queues address the problem based solely on the relative positions of the object in the queue; the first object in the queue is the first object out of the queue. Basic queues are well suited to model simple lines like the ones found in stores, the DMV, and movie theaters When other parameters such as degree of urgency impact the order in which the objects in the queue must be addressed, priority queuing is the answer. Priority queues pull objects from the queue based on measure of precedence known as priority. IT services and emergency rooms in hospital rooms often employ forms of priority queuing. Heaps are commonly used to implement a priority queue. The reason is because all elements in the heap are organized relative to a given heap order property. This property requires that items retrieved from the heap are either the smallest value in the heap (called a min heap), or the largest value in the heap (called a max heap). In other words, when retrieving data from a mirn heap, the element with the smallest value over all elements in the heap has priority and is removed first; the same holds for a max heap. The heap data structure is a complete binary tree, implemented as a static or dynamic array, where each subtree in the tree also follow the heap order property (i.e. the root is either the minimal or maximal value in that subtree) This exercise will focus on the potential use of priority queuing in emergency rooms. Hospital emergency rooms often divide the severity of their cases into five general levels from most urgent to least urgent: Code, Critical, Urgent, Non-urgent disabled, Ambulatory The Code level refers to someone who has suffered cardiac arrest outside of the hospital or someone whose vital signs crash within the emergency department [1]." It also refers to "people with gunshot or stab wounds with possible vital organ involvement and/or altered or absent vital signs [1]." Patients at the Code level bypass the management system and are taken directly to the next available trauma bed I.  Background Queuing is a problem which is commonly encountered in stores, movie theaters, IT services, and hospitals; many people or problems waiting in line to be addressed in an orderly and controlled fashion. Basic queues address the problem based solely on the relative positions of the object in the queue; the first object in the queue is the first object out of the queue. Basic queues are well suited to model simple lines like the ones found in stores, the DMV, and movie theaters When other parameters such as degree of urgency impact the order in which the objects in the queue must be addressed, priority queuing is the answer. Priority queues pull objects from the queue based on measure of precedence known as priority. IT services and emergency rooms in hospital rooms often employ forms of priority queuing. Heaps are commonly used to implement a priority queue. The reason is because all elements in the heap are organized relative to a given heap order property. This property requires that items retrieved from the heap are either the smallest value in the heap (called a min heap), or the largest value in the heap (called a max heap). In other words, when retrieving data from a mirn heap, the element with the smallest value over all elements in the heap has priority and is removed first; the same holds for a max heap. The heap data structure is a complete binary tree, implemented as a static or dynamic array, where each subtree in the tree also follow the heap order property (i.e. the root is either the minimal or maximal value in that subtree) This exercise will focus on the potential use of priority queuing in emergency rooms. Hospital emergency rooms often divide the severity of their cases into five general levels from most urgent to least urgent: Code, Critical, Urgent, Non-urgent disabled, Ambulatory The Code level refers to someone who has suffered cardiac arrest outside of the hospital or someone whose vital signs crash within the emergency department [1]." It also refers to "people with gunshot or stab wounds with possible vital organ involvement and/or altered or absent vital signs [1]." Patients at the Code level bypass the management system and are taken directly to the next available trauma bed