Question
My output doesn't match with the solution. Can you please check the code. I also put my output in here just in case if you
My output doesn't match with the solution. Can you please check the code. I also put my output in here just in case if you want to see what's not the same!


// C program to find approximate value of cos(x) using Taylor series
#include
#include
// function declaration
int factorial(int);
double power(double ,int);
double cos_N(double ,int);
double cos_delta(double,double);
int main(void) {
int m,option,iter;
double x,delta;
int i=1;
// file pointers for input and output file
FILE *fileptr= fopen("cos_input.dat","r");
FILE *outFile = fopen("cos_output.dat","w");
// if input file doesn't exist
if(fileptr == NULL)
printf("Unable to open file");
else{
fscanf(fileptr,"%d",&m); // read m
// read till the end of file
while(!feof(fileptr))
{
fscanf(fileptr,"%d",&option); // read the option
fscanf(fileptr,"%lf",&x); // read the value of x
// call cos_N
if(option==1)
{
fscanf(fileptr,"%d",&iter);
fprintf(outFile,"Case %d: cos(%lf) = %lf ",i,x,cos_N(x,iter));
fflush(stdout);
}else{ // call cos_delta
fscanf(fileptr,"%lf",&delta);
fprintf(outFile,"Case %d: cos(%lf) = %lf ",i,x,cos_delta(x,delta));
fflush(stdout);
}
i++;
}
}
// closing the files
fclose(fileptr);
fclose(outFile);
return EXIT_SUCCESS;
}
// function to calculate and return the factorial of a number
int factorial(int n)
{
int fact =1;
int i=1;
for(;i
}
fact=fact*i;
return fact;
}
// function to calculate and return the number raised to power n
double power(double x,int n)
{
double p = 1;
int i=0;
for(;i } p=p*x; return p; } // function to calculate the value of cos(x) given x and number of iterations double cos_N(double x,int n) { double cx=1; int i=1; for(;i } cx=cx+(((double)power(-1,i)*power(x,2*i))/factorial(2*i)); return cx; } // function to calculate the value of cos(x) given x and fixed precision double cos_delta(double x,double delta) { double cx,px,eps; int num=2; cx=1; px=0; int sf=-1; eps = cx - px; if(eps eps = -eps; while(eps > delta) { px=cx; cx = cx+((sf*power(x,num))/factorial(num)); eps = cx-px; if(eps eps =-eps; sf=-sf; num=num+2; } return cx; } // end of program 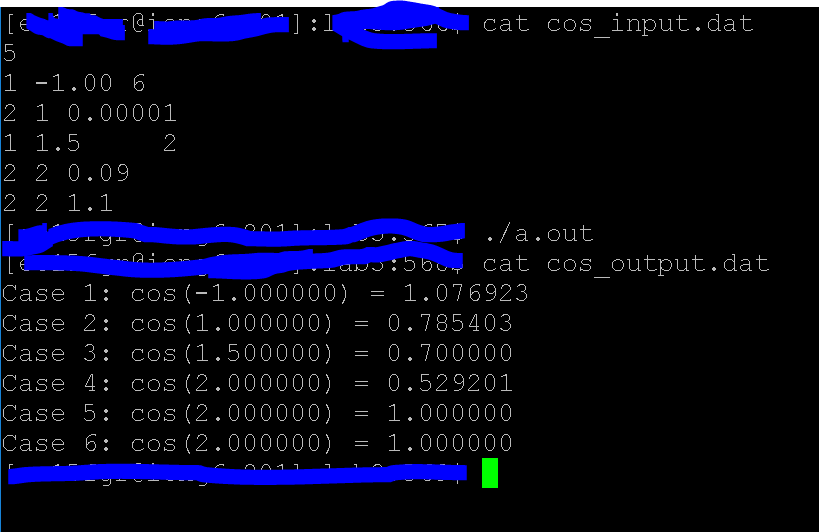
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


