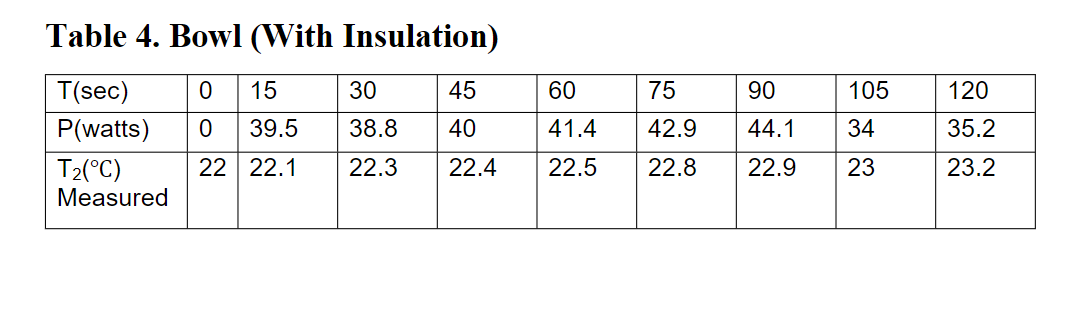
Name: Lab Date: Time: 3. Introduction The first law of thermodynamics states that heat and work are equivalent forms of energy, work can be transformed into heat and vice versa. This simple experiment is designed to examine that principle. A hand held food blender will be used as a source of mechanical work input to a bowl and a beaker containing water. The electric power into the blender is measured directly with an energy meter. The measured temperature rise in the water gives an indication of how this work is transformed into heat energy. However, there will be an imbalance between the work and heat. This does not mean that the first law of thermodynamics is invalid, rather it forces us to examine where the work and heat actually go. IY 1 - Engineering Thermodynamics Laboratory Experiment The Equivalence between Work and Heat 1. Objective To verify the equivalence between mechanical work and heat. To provide validation of the first law of thermodynamics. Applying the first law of thermodynamics for a non-flow process to this system consisting of a mass, m of fluid with specific heat capacity C, the difference between the heat crossing the boundary of a system AQ and the work crossing that boundary AW gives rise to a change in the internal energy of that system AU. This can be expressed as: - w - (1) ) 2.Equipment 1) 240V electric blender with beaker (Russell Hobbs Creations 3 in 1 Hand 1( Blender). See Figure 1. 2) Thermometer (Digitron TM22 thermocouple and readout). See Figure 2 3) Energy meter (PP-Energymeter). See Figure 3. 4) Stopwatch (Multi Function Timer Stop Watch On Cord) See Figure 4. To be consistent with AU = m (T2 - T:) where T2 and T. are the final and initial temperatures of the system, this needs to be written as: (Qin - Qoutl-Wout - Win) = m CT2 - Tu) (2) (2 In this experiment, there is no external source of heat applied to the system, Qin = 0 and no work is extracted from the system, Wout = 0, therefore: = We-Qout = m (T2 - T:) (3) Rearranging for the measured temperature T2 gives TET, W.-Q +- Q mc (4) Figure 1.240V Blender with beaker Figure 2. Thermocouple and Digital Readout For water at room temperature C = 4.18 kJ/kg K, or 4.18 J/g K, and the density 1000 kg/mor 1g/cm 4. Safety and Operation Warnings a) Be careful with the blades of the blender, these can seriously damage fingers and other parts of your body. Never operate the blender outside the bowl or beaker. b) Beware of water spilling onto any electric appliances as this may cause a short circuit and you may get a shock. Make sure that all electrical connections, cables and equipment are kept dry and away from water. c) Do not overheat the blender driver by running it longer time than necessary. Figure 3. Energy meter Figure 4. Stop watch 5. Experimental Procedure 1 2 8. Experimental Results Table 1. Experiment 1 - Mechanical work to heat in the beaker (without insulation) 1 Volume of water = t(sec 0 15 30 45 60 75 90 105 120 P (Watts) 1) Preparation - Identify the various pieces of equipment and verify it is complete (insulation materials and rubber bands to fix them are available). - Place approximately 0.3-0.4 litres of water in both the beaker and the bowl, make a note of the actual volume. Be ware that the tap water temperature may be quite different from the room temperature. - Select the power (Watts) option on the energy meter. - Set the time on the stopwatch to zero. - Connect power supply for the blender. - One person operates the blender, the other takes readings of temperature, power and time-decide who does what. - 2) Operation a) Experiment using the beaker without insulation Connect the thermocouple probe to the digital display, place the thermocouple into the beaker. Place the blender into the beaker, so that its weight is supported by the base, ensure the blades are clear of the thermocouple probe. Press and hold the lower power button (speed 2) for 2 minutes. Complete Table 1: the measured temperature, T("C), measured power, P and Work, W. = P x time(s). Let the motor cool for at least 5 minutes before using it again. Work, W. (Joules) Ta (C) Measured T: (C) By formula Table 2. Experiment 2- Mechanical work to heat in the beaker (with insulation) Volume of water = = b) Experiment using the beaker with insulation Empty the beaker, add new water, attach the insulation to the beaker with the rubber bands supplied. Add new water and repeat the procedure in 2a) and complete Table 2 with the new experiment results. Let the motor cool for at least 5 minutes before using it again. t(sec 0 0 15 30 45 60 75 90 105 120 P (Watts) c) Experiment using the bowl without insulation Connect the thermocouple probe, which is already attached to the bowl, to the digital display. Connect the blender to the bowl, ensure the blades are clear of the thermocouple probe. Press and hold the lower power button (speed 2) for 2 minutes. Complete Table 3 with new experiment results. Let the motor cool for at least 5 minutes before using it again. . d) Experiment using the bowl with insulation Empty the bowl, add new water, attach the insulation to the bowl with the rubber bands supplied. Repeat the procedure in 2c) and complete Table 4 with the new experiment results. Work, W. (Joules) T (C) Measured Ta (C) By formula 6. Theoretical calculation for temperature Ta Using Equation (4), assuming no heat losses by letting Qu=0 (what can be caused by this assumprion?), calculate Tzand enter these values into Tables 1, 2, 3 and 4. 7. Display of Results Plot the experimentally measured and theoretical temperatures Ta against Win from the 4 experiments on the graph papers given. Use appropriate legends and labels for points, curves and axis. 3 4 Beaker experiments: Temperature Ta (C) against work W. (Joules) Table 3.Experiment 3-Mechanical work to heat in the bowl (without insulation) Volume of water (sec) 10 15 30 45 60 75 90 105 120 P (Watts) Work, Win (Joules) Ta (C) Measured T: (C) By formula Table 4. Experiment 4 - Mechanical work to heat in the bowl (with insulation) Volume of water ised 0 15 30 45 60 75 90 105 120 P (Watts) Work, Win (Joules) Ta (C) Measured T: (C) By formula 9. Discussion Bowl experiments: Temperature T2 (C) against work Win (Joules) 1) Give qualitative reasons for the imbalance between Win and the change of internal energy. What constitutes Qout in the beaker and bowl experiments ? 2) Give a quantitative estimate of the percentage energy losses in converting electrical energy to heat energy to the water. 11. Appendix 3) The electricity used to drive the blender for this experiment came from a power station that burned fossil fuel to generate steam, which was expanded through a turbine and then powered the generator. If we were able to reverse this process it should be possible to use the heat stored in the water to drive a turbine to generate electricity in a similar way. Explain why this is not possible. A1. Joule's paddle wheel experiment The paddle wheel experiment was conducted by James Joule in 1843, in which he let a weight of 890 pounds (404 kg) fall through a height of one foot (0.3048 m), which worked (turned) a paddle wheel in a tub of water, thus causing a raise in temperature of one degree in the water, as measured by a thermometer. The measured variables: mass, height, temperature gave one of the first accurate measured of the mechanical equivalent of heat. The results were described in his famous 1845 paper "On the Mechanical Equivalent of Heat", in which Joule determined a value A for the amount of work W required to produce a unit of heat Q. 10. Conclusions (write this section using a maximum of 200 words) 10 Volume of water = 300 ml Data Set-1 75 90 105 120 Table 1. Beaker (Without Insulation) T(sec) 0 15 30 45 60 P(watts) 0 43 40.6 39.8 37.7 T2(C) 20.2 20.3 20.4 20.4 20.4 Measured 36.9 35.5 34.6 35.5 20.7 20.6 20.6 20.6 Table 2. Beaker (With Insulation) 0 15 30 45 60 75 90 105 120 0 25.1 24.6 25.2 25.1 24.9 24.9 25 25.2 T(sec) P(watts) T2(C) Measured 21.1 21.2 21.3 21.4 21.5 21.5 21.6 21.6 21.7 Table 3. Bowl (Without Insulation) 0 15 30 45 60 75 105 90 41.6 120 38 0 43.5 44 41.4 41.4 39.5 40 T(sec) P(watts) T2(C) Measured 23.5 23.5 23.5 23.6 23.8 23.8 24.1 24.3 24.4 Table 4. Bowl (With Insulation) 0 15 30 45 60 75 90 105 120 0 39.5 38.8 40 41.4 34 35.2 T(sec) P(watts) T2(C) Measured 42.9 22.8 44.1 22.9 22 22.1 22.3 22.4 22.5 23 23.2 Name: Lab Date: Time: 3. Introduction The first law of thermodynamics states that heat and work are equivalent forms of energy, work can be transformed into heat and vice versa. This simple experiment is designed to examine that principle. A hand held food blender will be used as a source of mechanical work input to a bowl and a beaker containing water. The electric power into the blender is measured directly with an energy meter. The measured temperature rise in the water gives an indication of how this work is transformed into heat energy. However, there will be an imbalance between the work and heat. This does not mean that the first law of thermodynamics is invalid, rather it forces us to examine where the work and heat actually go. IY 1 - Engineering Thermodynamics Laboratory Experiment The Equivalence between Work and Heat 1. Objective To verify the equivalence between mechanical work and heat. To provide validation of the first law of thermodynamics. Applying the first law of thermodynamics for a non-flow process to this system consisting of a mass, m of fluid with specific heat capacity C, the difference between the heat crossing the boundary of a system AQ and the work crossing that boundary AW gives rise to a change in the internal energy of that system AU. This can be expressed as: - w - (1) ) 2.Equipment 1) 240V electric blender with beaker (Russell Hobbs Creations 3 in 1 Hand 1( Blender). See Figure 1. 2) Thermometer (Digitron TM22 thermocouple and readout). See Figure 2 3) Energy meter (PP-Energymeter). See Figure 3. 4) Stopwatch (Multi Function Timer Stop Watch On Cord) See Figure 4. To be consistent with AU = m (T2 - T:) where T2 and T. are the final and initial temperatures of the system, this needs to be written as: (Qin - Qoutl-Wout - Win) = m CT2 - Tu) (2) (2 In this experiment, there is no external source of heat applied to the system, Qin = 0 and no work is extracted from the system, Wout = 0, therefore: = We-Qout = m (T2 - T:) (3) Rearranging for the measured temperature T2 gives TET, W.-Q +- Q mc (4) Figure 1.240V Blender with beaker Figure 2. Thermocouple and Digital Readout For water at room temperature C = 4.18 kJ/kg K, or 4.18 J/g K, and the density 1000 kg/mor 1g/cm 4. Safety and Operation Warnings a) Be careful with the blades of the blender, these can seriously damage fingers and other parts of your body. Never operate the blender outside the bowl or beaker. b) Beware of water spilling onto any electric appliances as this may cause a short circuit and you may get a shock. Make sure that all electrical connections, cables and equipment are kept dry and away from water. c) Do not overheat the blender driver by running it longer time than necessary. Figure 3. Energy meter Figure 4. Stop watch 5. Experimental Procedure 1 2 8. Experimental Results Table 1. Experiment 1 - Mechanical work to heat in the beaker (without insulation) 1 Volume of water = t(sec 0 15 30 45 60 75 90 105 120 P (Watts) 1) Preparation - Identify the various pieces of equipment and verify it is complete (insulation materials and rubber bands to fix them are available). - Place approximately 0.3-0.4 litres of water in both the beaker and the bowl, make a note of the actual volume. Be ware that the tap water temperature may be quite different from the room temperature. - Select the power (Watts) option on the energy meter. - Set the time on the stopwatch to zero. - Connect power supply for the blender. - One person operates the blender, the other takes readings of temperature, power and time-decide who does what. - 2) Operation a) Experiment using the beaker without insulation Connect the thermocouple probe to the digital display, place the thermocouple into the beaker. Place the blender into the beaker, so that its weight is supported by the base, ensure the blades are clear of the thermocouple probe. Press and hold the lower power button (speed 2) for 2 minutes. Complete Table 1: the measured temperature, T("C), measured power, P and Work, W. = P x time(s). Let the motor cool for at least 5 minutes before using it again. Work, W. (Joules) Ta (C) Measured T: (C) By formula Table 2. Experiment 2- Mechanical work to heat in the beaker (with insulation) Volume of water = = b) Experiment using the beaker with insulation Empty the beaker, add new water, attach the insulation to the beaker with the rubber bands supplied. Add new water and repeat the procedure in 2a) and complete Table 2 with the new experiment results. Let the motor cool for at least 5 minutes before using it again. t(sec 0 0 15 30 45 60 75 90 105 120 P (Watts) c) Experiment using the bowl without insulation Connect the thermocouple probe, which is already attached to the bowl, to the digital display. Connect the blender to the bowl, ensure the blades are clear of the thermocouple probe. Press and hold the lower power button (speed 2) for 2 minutes. Complete Table 3 with new experiment results. Let the motor cool for at least 5 minutes before using it again. . d) Experiment using the bowl with insulation Empty the bowl, add new water, attach the insulation to the bowl with the rubber bands supplied. Repeat the procedure in 2c) and complete Table 4 with the new experiment results. Work, W. (Joules) T (C) Measured Ta (C) By formula 6. Theoretical calculation for temperature Ta Using Equation (4), assuming no heat losses by letting Qu=0 (what can be caused by this assumprion?), calculate Tzand enter these values into Tables 1, 2, 3 and 4. 7. Display of Results Plot the experimentally measured and theoretical temperatures Ta against Win from the 4 experiments on the graph papers given. Use appropriate legends and labels for points, curves and axis. 3 4 Beaker experiments: Temperature Ta (C) against work W. (Joules) Table 3.Experiment 3-Mechanical work to heat in the bowl (without insulation) Volume of water (sec) 10 15 30 45 60 75 90 105 120 P (Watts) Work, Win (Joules) Ta (C) Measured T: (C) By formula Table 4. Experiment 4 - Mechanical work to heat in the bowl (with insulation) Volume of water ised 0 15 30 45 60 75 90 105 120 P (Watts) Work, Win (Joules) Ta (C) Measured T: (C) By formula 9. Discussion Bowl experiments: Temperature T2 (C) against work Win (Joules) 1) Give qualitative reasons for the imbalance between Win and the change of internal energy. What constitutes Qout in the beaker and bowl experiments ? 2) Give a quantitative estimate of the percentage energy losses in converting electrical energy to heat energy to the water. 11. Appendix 3) The electricity used to drive the blender for this experiment came from a power station that burned fossil fuel to generate steam, which was expanded through a turbine and then powered the generator. If we were able to reverse this process it should be possible to use the heat stored in the water to drive a turbine to generate electricity in a similar way. Explain why this is not possible. A1. Joule's paddle wheel experiment The paddle wheel experiment was conducted by James Joule in 1843, in which he let a weight of 890 pounds (404 kg) fall through a height of one foot (0.3048 m), which worked (turned) a paddle wheel in a tub of water, thus causing a raise in temperature of one degree in the water, as measured by a thermometer. The measured variables: mass, height, temperature gave one of the first accurate measured of the mechanical equivalent of heat. The results were described in his famous 1845 paper "On the Mechanical Equivalent of Heat", in which Joule determined a value A for the amount of work W required to produce a unit of heat Q. 10. Conclusions (write this section using a maximum of 200 words) 10 Volume of water = 300 ml Data Set-1 75 90 105 120 Table 1. Beaker (Without Insulation) T(sec) 0 15 30 45 60 P(watts) 0 43 40.6 39.8 37.7 T2(C) 20.2 20.3 20.4 20.4 20.4 Measured 36.9 35.5 34.6 35.5 20.7 20.6 20.6 20.6 Table 2. Beaker (With Insulation) 0 15 30 45 60 75 90 105 120 0 25.1 24.6 25.2 25.1 24.9 24.9 25 25.2 T(sec) P(watts) T2(C) Measured 21.1 21.2 21.3 21.4 21.5 21.5 21.6 21.6 21.7 Table 3. Bowl (Without Insulation) 0 15 30 45 60 75 105 90 41.6 120 38 0 43.5 44 41.4 41.4 39.5 40 T(sec) P(watts) T2(C) Measured 23.5 23.5 23.5 23.6 23.8 23.8 24.1 24.3 24.4 Table 4. Bowl (With Insulation) 0 15 30 45 60 75 90 105 120 0 39.5 38.8 40 41.4 34 35.2 T(sec) P(watts) T2(C) Measured 42.9 22.8 44.1 22.9 22 22.1 22.3 22.4 22.5 23 23.2