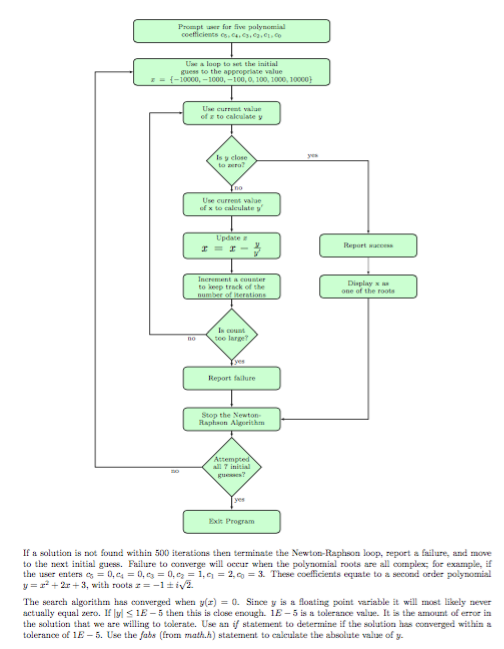
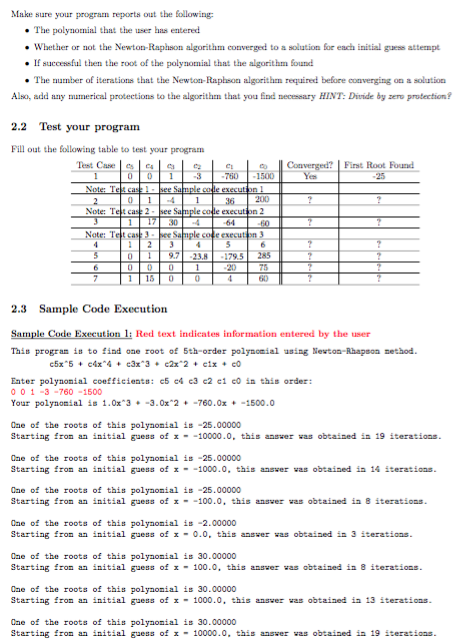
Need help with a C program with comments so i understand what you're doing, using the formate printf("..
not cout
The graph is just a way to look at the code and there are some samples to test the code. Would perfer to have the same wording as the examples given.
2 Polynomial Root Calculation: Problem Description Engineers often need to calculate the roots of a given polynomial. For low order polynomials these computations can be done by hand. For higher order polynonials these calculations can be cumbersome, if not impossible, without the use of a computer. One computational method of finding real roots of a polynomial is the Newton-Raphson algorithm. We wish to write a C program that uss the Newton-Raphson method for caleulating the roots of a polynomial Although this program will not be able to solve for complex roots, it will be able to calculate real roots; maybe later we can adjust the routine to include complex roota. Since it is ponsible that the polynomial roots are all complex, Le. no renl roots at all, it may be that the Newton Raphson routine fnils to converge 2.1 Newton-Raphson Algorithm: of a 5eh-order polynomial Write a progrun that prompts the user to input the coefficients es,e, The % order polynomnial has the form We know that the first derivative of y with respeet to r i We ean use this information to ind the roots of the polynomial. The baale den, in the Newton-Raphson method, as follown: (a) Given an initial guessz, and polynomial coefficients e, caleulate y (b) Check to see if y is close enough to zero, ie. within some snall tolerance close to zero. (i) If so then terminate. Algorithm has converged! i) If not then continue (e) Use the current value of r to caleulate (d) Create new guess for z using the update formula z = z- (e) Increment a counter to count the number of algorithm iterations (E) Check to see if the mamber of iterations has exceeded a count limit (say 500) (i) If so then terminate. Algorithm has failed (ii) If not then return to step We would like to use 7 different initial guesses to test the Newton-Raphson algorithn: XinitiaiGves-10000,-1000,-100,0, 100, 1000, 10000H Thus your od will need to loop around the Newton-Raphson algorithn 7 times, once for each initial guess. This same information is described in the flow chart below
