Question: Need help with CSE 205 Java project Here are the included Java classes Main: mport javax.swing.JFrame; /** * The Main class containing the main() and
Need help with CSE 205 Java project




![void main(String[] args) { new Main().run(); } /** * exit() is called](https://s3.amazonaws.com/si.experts.images/answers/2024/09/66ddd959c1a4a_12966ddd95932c39.jpg)

Here are the included Java classes
Main:
mport javax.swing.JFrame;
/** * The Main class containing the main() and run() methods. */ public class Main {
// A reference to the View object. private View mView;
/** * This is where execution starts. Instantiate a Main object and then call run(). */ public static void main(String[] args) { new Main().run(); }
/** * exit() is called when the Exit button in the View is clicked. Call System.exit(0). */ public void exit() { System.exit(0); }
/** * Accessor method for mView. */ private View getView() { return mView; }
/** * run() is the main routine. */ private void run() { JFrame.setDefaultLookAndFeelDecorated(true); setView(new View(this)); }
/** * Mutator method for mView. */ private void setView(View pView) { mView = pView; }
}
BinartOperator.java:
/** * BinaryOperator is the superclass of all binary operators. */ public abstract class BinaryOperator extends Operator {
public BinaryOperator() { }
/** * Called to evaluate the operator. */ public abstract Operand evaluate(Operand pLhsOperand, Operand pRhsOperand);
/** * Returns true since all subclasses of BinaryOperator are binary operators. */ @Override public boolean isBinaryOperator() { return true; }
}
AddOperator.java:
/** * Represents the addition operator which is a specific type of binary operator. */ public class AddOperator extends BinaryOperator {
public AddOperator() { }
/** * Returns the sum of the left-hand side operand and the right-hand side operand. */ @Override public Operand evaluate(Operand pLhsOperand, Operand pRhsOperand) { return new Operand(pLhsOperand.getValue() + pRhsOperand.getValue()); }
/** * Returns the normal precedence level of this operator. */ @Override public int precedence() { return 2; }
/** * Returns the precedence level of this operator when on it is on the operator stack. */ @Override public int stackPrecedence() { return 2; }
}
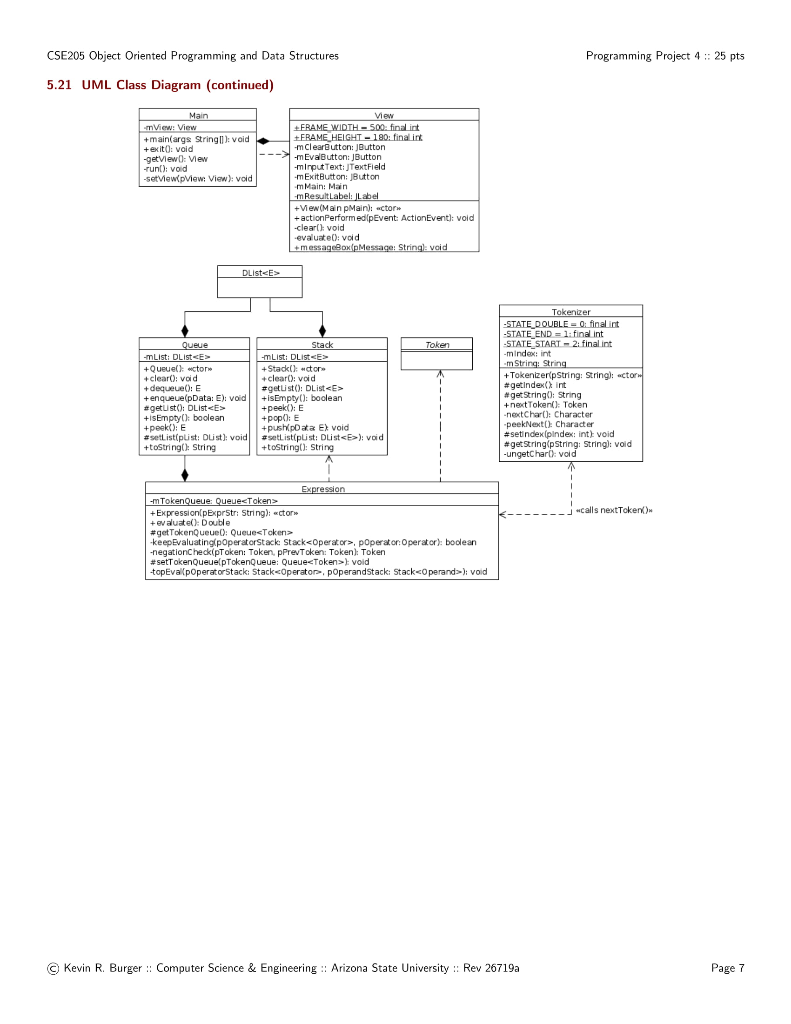
CSE205 Object Oriented Programming and Data Structures Programming Project 4 :: 25 pts 1 Submission Instructions Create a folder named asuriteid-p04 where asuriteid is your ASURITE user id (for example, if your ASURITE user id is jsmith then your folder would be named jsmith6-p04) and copy all of your java source code files to this folder. Do not copy the class files or any other files. Next, compress the asuriteid-p04 folder creating a zip archive file named asuriteid-p04. zip (c.g., jsmith6-p01.zip). Upload asuritcid-p01.zip on the Canvas Module 7: P2 Duc submission page before the project deadline. Please see the Course Summary section on the Syllabus page in Canvas for the deadline. Consult the Syllabus for the late and academic integrity policies. 2 Learning Objectives 1. Complete all of the learning objects of the previous projects. 2. To implement a GUI interface and respond to action events, 3. To use the linked list, stack, and queue classes. 3 Background In the lecture notes and video lectures for Stacks and Queues : Sections 3 - 7 we discussed an application that evaluates an arithmetic expression written in infix notation such as: (-1 - -2) * -(3/5) Infix notation is the usual algebraic notation that we are all familiar with where a binary operator (a binary operator is an operator that has two operands) is written between the left-hand and right-hand operands. For example, in the expression above, the left-hand operand of the subtraction operator is -1 and the right-hand operand is -2. Some operators, such as the negation operator, are unary operators meaning there is only one operand (uni = one). For negation, the operand is written to the right of the negation operator. Therefore, this expression contains six operators: negation, subtraction, negation, multiplication, negation, and division. In the algorithm that evaluates the expression, we also treat a left parenthesis as an operator, which it is not, but during the evaluation we have to push left parentheses onto the operator stack. In an infix arithmetic expression, cach operator has a precedence level, which for a left parenthesis, is different when it is on the operator stack as opposed to when it is not (this will become clear when you read the trace of the algorithm for the above expression; see page 3): Operator Normal Precedence Level Stack Precedence Level Right parentheses really don't have precedence because they are not pushed on the operator stack, but we assign them a precedence level of 1 for consistency. The algorithm discussed in the notes did not handle the negation operator so I have modified it to handle negation. Here is the revised algorithun: Method evaluate(In: papr as an infix expression) Returns Double Create operator Stack -- Stores Operators Create operardStack -- Stores Operands While end of Expr has not been reached Do Scan next loken in pb.pr -- The type of Loken is Token Kevin R. Burger: Computer Science & Engineering : Arizona State University :: Rev 26719a Page 1 CSE205 Object Oriented Programming and Data Structures Programming Project 4 :: 25 pts If token is an operand Then Convert token to Operand object named number operu. Slack.push(newber) ElseIf token is an InstanceOf Left Paren Then Convert token to Lefl Paren object named paren operator Stack.push(paren) ElseIf loken is an InstanceOf Right Paven Then While not operator Stack.peck) is an InstanceOf Left Paren Do top Eval) operator Stack.pop() - Pops the Left Paren ElseIf token is Negation, Addition, Subtraction, Multiplication, or Division Then Convert token to Operator object named operator While keep Ewaluating) returns True Do top Full operator Stack.push(op) End While While not operator Stack.isEmpty() Do top Eval() Return operandStack.pop() -- the result of evaluating the expression End Method evaluate Method keep Evaluating Returns True or False If operator Stack.is Empty The Return False Else Return stack Precedence operator Stack.peckO) 2 precedence operator) End Method keep Evaluating Method lopEval() Returns Nothing right operandStack.popo operator operatorStack.pop() If operator is Negation Then operandStack.push(-right) Else left operandStack.pop() If operator is Addition Then operandStack push(left-right) ElseIf operator is Subtraction Then operandStack.push(left-right) ElseIf operator is Mullaplication Then operandSlack.push(left * right) Else operandStack.push(left, right) End If End Method top val Method precedence(In: Operator pOperator) Returns Int If pOperator is LeftPoren Then Return 5 ElseIf pOxeralor is Negation Then Return 4 ElseIf pOperator is Multiplication or Division The Return 3 ElseIf pOperator is Addition or Subtraction Then Return 2 Else Return 1 End Method prevelence Method stack PrecedenceIn: Operator pOperator) Returns Int If Operator is LeftParen. Then Return 0 ElseIf pOperator is Negation Then Return 4 ElseIf pOperator is Multiplication or Division Then Return 3 ElseIf p Operator is Addition or Subtraction Then Return 2 Else Return 1 End Method stack Precedence Kevin R. Burger: Computer Science & Engineering : Arizona State University :: Rev 26719a Page 2 CSE205 Object Oriented Programming and Data Structures Programming Project 4 :: 25 pts It would be worthwhile to trace the algorithm using the above expression to make sure you understand how it works: 1. Create the operand and operator stacks. Both are empty at the beginning. 2. Scan the first token and push it onto the operator stack. 3. Scan the next token - (negation) and push it onto the operator stack. 4. Scan the next token 1 and push it onto the operand stack. 5. Scan the next token - (subtraction). Since the operator on top of the operator stack (negation) has higher precedence than subtraction, evaluate the top (note: negation is a unary operator so there is only one operand to be popped from the operand stack): a. Pop the top number from the operand stack. Call this right = 1. b. Pop the top operator from the operator stack. Call this operator = - (negation). c. Evaluate operator and push the result (-1) onto the operand stack. d. Now push the subtraction opcrator onto the operator stack. Scan the next token - (negation). Since the operator on top of the stack (subtraction) has precedence less than ncgation, push the negation operator onto the operator stack. 7. Scan the next token 2 and push it onto the operand stack. 8. Scan the next token ). Pop and evaluate operators from the operator stack until the matching is reached. a. The top operator is a unary operator (negation): Pop the top number from the operand stack. Call this right = 2. Pop the top operator from the operator stack. Call this operator = - (negation). Evaluate operator and push the result (-2) onto the operand slack. b. The top operator is a binary operator (subtraction): Pop the top number from the operand stack. Call this right = -2. Pop the top number from the operand stack. Call this left = -1. Pop the top operator from the operator stack. Call this operator = - (subtraction). Evaluate operator and push the result (1) onto the operand stack. c. The top operator is ( so pop it. 9. Scan the next token * (multiplication). The operator stack is empty so push * 10. Scan the next token - (negation). Since negation has higher precedence than the operator on top of the operator stack (multiplication) push the negation operator onto the operator stack, 11. Scan the next token ( and push it onto the operator stack. 12. Scan the next token 3 and push it onto the operand stack. 13. Scan the next token/ (division). Since the operator on top of the stack (left parenthesis) has higher precedence than division push / onto the operator stack. Now do you see why the precedence of changes when it is on the operator stack? 14. Scan the next token 5 and push it onto the operand stack. 15. Scan the next token ). Pop and evaluate operators from the operator stack until the matching is reached. a. The top operator is binary operator (division) Pop the top number from the operand stack. Call this right = 5. Pop the top number from the operand stack. Call this left = 3. Pop the top operator from the operator stack. Call this operator = !. Evaluate operator and push the result (0.6) onto the operand stack. b. The top operator is so pop it. 16. The end of the infix expression string has been reached. Pop and evaluate operators from the operator stack until the operator stack is empty. a. The top operator is a unary operator (negation): Pop the top number from the operand stack. Call this right = 0.6. Pop the top operator from the operator stack. Call this operator - - (negation). Evaluate operator and push the result (-0.6) onto the operand stack. Kevin R. Burger: Computer Science & Engineering : Arizona State University :: Rev 26719a Page 3 CSE205 Object Oriented Programming and Data Structures Programming Project 4 :: 25 pts b. The top operator is a binary operator (multiplication): Pop the top number from the operand stack. Call this right = -0.6. Pop the top number from the operand stack. Call this left = 1. Pop the top operator from the operator stack. Call this operator = * Evaluate operator and push the result (-0.6) onto the operand stack. 17. The operator stack is empty. Pop the result from the operand stack (-0.6) and return it. 4 Software Requirements The project shall implement a GUI calculator which accepts as input a syntactically correct arithmetic expression written in infix notation and displays the result of evaluating the expression. The program shall meet these requirements. 1. The program shall implement a GUI which permits the user to interact with the calculator. Watch the Project 4 video lecture for a demonstration of how the application works. 2. When the Clear button is clicked, the input text field and the result label shall be configured to display nothing. 3. When a syntactically correct infix arithmetic expression is entered in the input text field and the Evaluate button is clicked, the program shall evaluate the expression and display the result in the label of the GUI. 4. When the input text field is empty, clicking the Evaluate button does nothing. 5. When the Exit button is clicked, the application shall terminate. 6. Note: you do not have to be concerned with syntactically incorrect infix expressions. We will not test your program with such expressions. 5 Software Design Refer to the UML class diagram in Section 5.21. Your program shall implement this design. 5.1 Main Class The Main class shall contain the main() method which shall instantiate an object of the Main class and call run() on that object. Main is completed for you. 5.2 AddOperator Implements the addition operator, which is a binary operator. AddOperator is completed for you. Use AddOperator as a guide when completing DivOperutor, MultOperator, and Sub Operator. 5.3 BinaryOperator The abstract superclass of all binary operators. BinaryOperator is completed for you. Note that Binary Operator imple- ments one abstract method evaluate() which all subclasses must implement. The subclasses are AddOperator, DivOperator, MultOperator, and Sub Operator. 5.4 DivOperator Implements the division operator, which is a binary operator. Complete the code in this file by using the AddOperator class as an example. 5.5 DList This is the DLisk class from the Module 7 Source Code vip archive. It implements a generic doubly linked list where the data type of cach list clement is E. DList is completed for you. For example, to create a DList which stores elements of the type Token you would write DList list - new DListo ; much in the same way that we can create an ArrayList of Doubles by writing ArrayList list = new ArrayListo ; 5.6 Expression Represents an infix expression to be evaluated. Use the provided pseudocode as a guide in completing this class Kevin R. Burger :: Computer Science & Engineering :: Arizona State University :: Rev 26719a Page 4 CSE205 Object Oriented Programming and Data Structures Programming Project 4 :: 25 pts 5.7 LeftParen Represents a left parenthesis in the expression. LeftParen is completed for you. Note that LeftParen is a subclass of the abstract class Parenthesis. 5.8 MultOperator Implements the multiplication operator, which is a binary operator. Complete the code in this file by using the AddOperat- or class as an example. 5.9 Neg Operator Implements the negation operator, which is a unary operator. Complete the code in this file by using the AddOperator class as an example. Note, however, that negation is a unary operator so it only has one operand. 5.10 Operand An operand is a numeric value represented as a Double. Implement the class using the UML class diagram as a guide. 5.11 Operator Operator is the abstract superclass of all binary and unary operators, i.e., it is the superclass of BinaryOperator and UnaryOperator. Implement the class using the UML class diagram as a guide. Note that all of the non-constructor methods are abstract, i.c., none of them are implemented in Operator: 5.12 Parenthesis Parenthesis is the superclass of Left Paren and Right Paren. These are treated as a weird sort of Operator because we need to be able to push Left Parens on the operator stack when evaluating the expression. Parenthesis is completed for you. 5.13 Queue Implements a generic queue data structure using a DList list to store the elements. This is the same class that was provided in the Week 7 Source zip archive. Queue is completed for you. 5.14 Right Paren Represents a right parenthesis in the expression. Righ/Paren is completed for you. 5.15 Stack Implements a generic stack data structure using a DList list to store the elements. This is the same class that was provided in the Module 7 Source zip archive. Stack is completed for you. 5.16 SubOperator Implements the subtraction operator, which is a binary operator. Complete the code in this file by using the Add Operator class as an example. 5.17 Token Token is the abstract superclass of the different types of tokens (i.c., symbols) that can appear in an infix expression. Token is completed for you. 5.18 Tokenizer The Tokenizer class scans a String containing an infix expression and breaks it into tokens. For this project, a token will be either an Operand (a double value), a Left Paren or Right Paren, or an arithmetic UnaryOperator (subclass Neg Operator) or BinaryOperator (one of the AddOperator, Sub Operator, MultOperator, or DivOperator subclasses). Tokenizer is com- pleted for you. It is implemented as a finite state machine (FSM) which are commonly used in computing, especially when breaking a "sentence" of words or symbols into its component parts. If you have the time, you should study the code to learn how FSM's work and are used. Kevin R. Burger: Computer Science & Engineering : Arizona State University :: Rev 26719a Page 5 CSE205 Object Oriented Programming and Data Structures Programming Project 4 :: 25 pts 5.19 Unary Operator Unary Operator is the superclass of all unary operators. Unary Operator is completed for you. 5.20 View The View implements the GUI. Read the comments and implement the pseudocode. 5.21 UML Class Diagram The UML class diagram is provided in the zip archive/url folder as two UMLet files. Because the images in this document are small, there are PNG images of the two class diagrams in the image folder. Your program shall implement this design. + Token(): wtore Operand mValue: Double + Operand(pvalue Double) uctor +qetValue(): Double + setValue(pvalue Double): void Operator + Operator) wctor + is BinaryOperator: boolean precedenceint +StackPrecedence): int 44 Parenthesis +Parenthesis actore +is BinaryOperator() boolean BinaryOperator UnaryOperator +UnaryOperator: ectors evaluate poperard: Operand: Operand + is BinaryOperator'x boolean +Binary Operator(): actor ev alatepthsoperand. Operand, phsoperand: Operand): Operand + is Binary Operator> boolean AAAA Left Paren +LeftParen), wctors + precedence(): int + stackPrecedence int NegOperator + NegOperator): ctor + evaluate Operand: Operand): Operand + precedence(): int + StackPrecedenceint Addoperator + Addoperator): actor + evaluatepths perand: Operand, phsoperand Operand): Operand + precedence(): int + stackPrecedenced in Right Paren +RightParen) wctor + precedence(): int + stackPrecedence int DivOperator + DivOperator): uctor + evaluate puhso perand: Operand, prhso peranch Operand): Operand + precedence(): int + stackPrecedence in Mult Operator + MultOperator): Token Queue -mList: DList +Queuel) actor +clear(); void +dequeue(): E +enqueue(pData: E); void #getuisto: DList +IsEmpty(): boolean peek(): E #setlist(pust: Dust): void +toString(): String Stack -mList: DLISTES +Stack .ctor + clear(); void getList(): DList +isEmpty(): boolean +peek) E +pop(): E +pushpData Ex void setListiplist: DList); void +toString(): String Tokenizer -STATE DOUBLE = 0; final int -STATE ENDl final int -STATE START - 2. final int -mindex: int -mStrings String +Tokenizer pString: String): actor #getindex(int #getString: String + nextToken() Token -nect Char(): Character -peekNext(): Character #setindexpindex: int void #getString(pString: Stringl: vold -ungetChard) void - calls nextToken() Expression -m Tokenqueue: Queue Token + Expression pexprstr String): ector + evaluate(): Double #getTokenQueue). Queues Token -keep Evaluating OperatorstackStack pOperator Operator): boolean -negationCheckipToken: Token pPrevToken: Tokenl: Token #setTokenQueuelpTokenQueue: QueuedToken>void topEval Operator Stack: Stack Operator, poperandStack: Stack Operand); void Kevin R. Burger: Computer Science & Engineering : Arizona State University : Rev 26719a Page 7 CSE205 Object Oriented Programming and Data Structures Programming Project 4 :: 25 pts 6 Additional Project Requirements 1. Format your code neatly. Use proper indentation and spacing. Study the examples in the book and the examples the instructor presents in the lectures and posts on the course website. 2. Put a comment header block at the top of each method formatted thusly: * A brief description of what the method does. */ Put a comment header block at the top of each source code file formatted thusly (or use /** ... */ comments if you wish): //*************** ******************************************************************** 1/ CLASS: classname (classname.java) // COURSE AND PROJECT INFO // CSE205 Object Oriented Programming and Data Structures, semester and year // Project Number: project number // AUTHOR: your name, your-asurite-id, your-email-addr //********* Kevin R. Burger: Computer Science & Engineering :: Arizona State University : Rev 26719a Page 8 CSE205 Object Oriented Programming and Data Structures Programming Project 4 :: 25 pts 1 Submission Instructions Create a folder named asuriteid-p04 where asuriteid is your ASURITE user id (for example, if your ASURITE user id is jsmith then your folder would be named jsmith6-p04) and copy all of your java source code files to this folder. Do not copy the class files or any other files. Next, compress the asuriteid-p04 folder creating a zip archive file named asuriteid-p04. zip (c.g., jsmith6-p01.zip). Upload asuritcid-p01.zip on the Canvas Module 7: P2 Duc submission page before the project deadline. Please see the Course Summary section on the Syllabus page in Canvas for the deadline. Consult the Syllabus for the late and academic integrity policies. 2 Learning Objectives 1. Complete all of the learning objects of the previous projects. 2. To implement a GUI interface and respond to action events, 3. To use the linked list, stack, and queue classes. 3 Background In the lecture notes and video lectures for Stacks and Queues : Sections 3 - 7 we discussed an application that evaluates an arithmetic expression written in infix notation such as: (-1 - -2) * -(3/5) Infix notation is the usual algebraic notation that we are all familiar with where a binary operator (a binary operator is an operator that has two operands) is written between the left-hand and right-hand operands. For example, in the expression above, the left-hand operand of the subtraction operator is -1 and the right-hand operand is -2. Some operators, such as the negation operator, are unary operators meaning there is only one operand (uni = one). For negation, the operand is written to the right of the negation operator. Therefore, this expression contains six operators: negation, subtraction, negation, multiplication, negation, and division. In the algorithm that evaluates the expression, we also treat a left parenthesis as an operator, which it is not, but during the evaluation we have to push left parentheses onto the operator stack. In an infix arithmetic expression, cach operator has a precedence level, which for a left parenthesis, is different when it is on the operator stack as opposed to when it is not (this will become clear when you read the trace of the algorithm for the above expression; see page 3): Operator Normal Precedence Level Stack Precedence Level Right parentheses really don't have precedence because they are not pushed on the operator stack, but we assign them a precedence level of 1 for consistency. The algorithm discussed in the notes did not handle the negation operator so I have modified it to handle negation. Here is the revised algorithun: Method evaluate(In: papr as an infix expression) Returns Double Create operator Stack -- Stores Operators Create operardStack -- Stores Operands While end of Expr has not been reached Do Scan next loken in pb.pr -- The type of Loken is Token Kevin R. Burger: Computer Science & Engineering : Arizona State University :: Rev 26719a Page 1 CSE205 Object Oriented Programming and Data Structures Programming Project 4 :: 25 pts If token is an operand Then Convert token to Operand object named number operu. Slack.push(newber) ElseIf token is an InstanceOf Left Paren Then Convert token to Lefl Paren object named paren operator Stack.push(paren) ElseIf loken is an InstanceOf Right Paven Then While not operator Stack.peck) is an InstanceOf Left Paren Do top Eval) operator Stack.pop() - Pops the Left Paren ElseIf token is Negation, Addition, Subtraction, Multiplication, or Division Then Convert token to Operator object named operator While keep Ewaluating) returns True Do top Full operator Stack.push(op) End While While not operator Stack.isEmpty() Do top Eval() Return operandStack.pop() -- the result of evaluating the expression End Method evaluate Method keep Evaluating Returns True or False If operator Stack.is Empty The Return False Else Return stack Precedence operator Stack.peckO) 2 precedence operator) End Method keep Evaluating Method lopEval() Returns Nothing right operandStack.popo operator operatorStack.pop() If operator is Negation Then operandStack.push(-right) Else left operandStack.pop() If operator is Addition Then operandStack push(left-right) ElseIf operator is Subtraction Then operandStack.push(left-right) ElseIf operator is Mullaplication Then operandSlack.push(left * right) Else operandStack.push(left, right) End If End Method top val Method precedence(In: Operator pOperator) Returns Int If pOperator is LeftPoren Then Return 5 ElseIf pOxeralor is Negation Then Return 4 ElseIf pOperator is Multiplication or Division The Return 3 ElseIf pOperator is Addition or Subtraction Then Return 2 Else Return 1 End Method prevelence Method stack PrecedenceIn: Operator pOperator) Returns Int If Operator is LeftParen. Then Return 0 ElseIf pOperator is Negation Then Return 4 ElseIf pOperator is Multiplication or Division Then Return 3 ElseIf p Operator is Addition or Subtraction Then Return 2 Else Return 1 End Method stack Precedence Kevin R. Burger: Computer Science & Engineering : Arizona State University :: Rev 26719a Page 2 CSE205 Object Oriented Programming and Data Structures Programming Project 4 :: 25 pts It would be worthwhile to trace the algorithm using the above expression to make sure you understand how it works: 1. Create the operand and operator stacks. Both are empty at the beginning. 2. Scan the first token and push it onto the operator stack. 3. Scan the next token - (negation) and push it onto the operator stack. 4. Scan the next token 1 and push it onto the operand stack. 5. Scan the next token - (subtraction). Since the operator on top of the operator stack (negation) has higher precedence than subtraction, evaluate the top (note: negation is a unary operator so there is only one operand to be popped from the operand stack): a. Pop the top number from the operand stack. Call this right = 1. b. Pop the top operator from the operator stack. Call this operator = - (negation). c. Evaluate operator and push the result (-1) onto the operand stack. d. Now push the subtraction opcrator onto the operator stack. Scan the next token - (negation). Since the operator on top of the stack (subtraction) has precedence less than ncgation, push the negation operator onto the operator stack. 7. Scan the next token 2 and push it onto the operand stack. 8. Scan the next token ). Pop and evaluate operators from the operator stack until the matching is reached. a. The top operator is a unary operator (negation): Pop the top number from the operand stack. Call this right = 2. Pop the top operator from the operator stack. Call this operator = - (negation). Evaluate operator and push the result (-2) onto the operand slack. b. The top operator is a binary operator (subtraction): Pop the top number from the operand stack. Call this right = -2. Pop the top number from the operand stack. Call this left = -1. Pop the top operator from the operator stack. Call this operator = - (subtraction). Evaluate operator and push the result (1) onto the operand stack. c. The top operator is ( so pop it. 9. Scan the next token * (multiplication). The operator stack is empty so push * 10. Scan the next token - (negation). Since negation has higher precedence than the operator on top of the operator stack (multiplication) push the negation operator onto the operator stack, 11. Scan the next token ( and push it onto the operator stack. 12. Scan the next token 3 and push it onto the operand stack. 13. Scan the next token/ (division). Since the operator on top of the stack (left parenthesis) has higher precedence than division push / onto the operator stack. Now do you see why the precedence of changes when it is on the operator stack? 14. Scan the next token 5 and push it onto the operand stack. 15. Scan the next token ). Pop and evaluate operators from the operator stack until the matching is reached. a. The top operator is binary operator (division) Pop the top number from the operand stack. Call this right = 5. Pop the top number from the operand stack. Call this left = 3. Pop the top operator from the operator stack. Call this operator = !. Evaluate operator and push the result (0.6) onto the operand stack. b. The top operator is so pop it. 16. The end of the infix expression string has been reached. Pop and evaluate operators from the operator stack until the operator stack is empty. a. The top operator is a unary operator (negation): Pop the top number from the operand stack. Call this right = 0.6. Pop the top operator from the operator stack. Call this operator - - (negation). Evaluate operator and push the result (-0.6) onto the operand stack. Kevin R. Burger: Computer Science & Engineering : Arizona State University :: Rev 26719a Page 3 CSE205 Object Oriented Programming and Data Structures Programming Project 4 :: 25 pts b. The top operator is a binary operator (multiplication): Pop the top number from the operand stack. Call this right = -0.6. Pop the top number from the operand stack. Call this left = 1. Pop the top operator from the operator stack. Call this operator = * Evaluate operator and push the result (-0.6) onto the operand stack. 17. The operator stack is empty. Pop the result from the operand stack (-0.6) and return it. 4 Software Requirements The project shall implement a GUI calculator which accepts as input a syntactically correct arithmetic expression written in infix notation and displays the result of evaluating the expression. The program shall meet these requirements. 1. The program shall implement a GUI which permits the user to interact with the calculator. Watch the Project 4 video lecture for a demonstration of how the application works. 2. When the Clear button is clicked, the input text field and the result label shall be configured to display nothing. 3. When a syntactically correct infix arithmetic expression is entered in the input text field and the Evaluate button is clicked, the program shall evaluate the expression and display the result in the label of the GUI. 4. When the input text field is empty, clicking the Evaluate button does nothing. 5. When the Exit button is clicked, the application shall terminate. 6. Note: you do not have to be concerned with syntactically incorrect infix expressions. We will not test your program with such expressions. 5 Software Design Refer to the UML class diagram in Section 5.21. Your program shall implement this design. 5.1 Main Class The Main class shall contain the main() method which shall instantiate an object of the Main class and call run() on that object. Main is completed for you. 5.2 AddOperator Implements the addition operator, which is a binary operator. AddOperator is completed for you. Use AddOperator as a guide when completing DivOperutor, MultOperator, and Sub Operator. 5.3 BinaryOperator The abstract superclass of all binary operators. BinaryOperator is completed for you. Note that Binary Operator imple- ments one abstract method evaluate() which all subclasses must implement. The subclasses are AddOperator, DivOperator, MultOperator, and Sub Operator. 5.4 DivOperator Implements the division operator, which is a binary operator. Complete the code in this file by using the AddOperator class as an example. 5.5 DList This is the DLisk class from the Module 7 Source Code vip archive. It implements a generic doubly linked list where the data type of cach list clement is E. DList is completed for you. For example, to create a DList which stores elements of the type Token you would write DList list - new DListo ; much in the same way that we can create an ArrayList of Doubles by writing ArrayList list = new ArrayListo ; 5.6 Expression Represents an infix expression to be evaluated. Use the provided pseudocode as a guide in completing this class Kevin R. Burger :: Computer Science & Engineering :: Arizona State University :: Rev 26719a Page 4 CSE205 Object Oriented Programming and Data Structures Programming Project 4 :: 25 pts 5.7 LeftParen Represents a left parenthesis in the expression. LeftParen is completed for you. Note that LeftParen is a subclass of the abstract class Parenthesis. 5.8 MultOperator Implements the multiplication operator, which is a binary operator. Complete the code in this file by using the AddOperat- or class as an example. 5.9 Neg Operator Implements the negation operator, which is a unary operator. Complete the code in this file by using the AddOperator class as an example. Note, however, that negation is a unary operator so it only has one operand. 5.10 Operand An operand is a numeric value represented as a Double. Implement the class using the UML class diagram as a guide. 5.11 Operator Operator is the abstract superclass of all binary and unary operators, i.e., it is the superclass of BinaryOperator and UnaryOperator. Implement the class using the UML class diagram as a guide. Note that all of the non-constructor methods are abstract, i.c., none of them are implemented in Operator: 5.12 Parenthesis Parenthesis is the superclass of Left Paren and Right Paren. These are treated as a weird sort of Operator because we need to be able to push Left Parens on the operator stack when evaluating the expression. Parenthesis is completed for you. 5.13 Queue Implements a generic queue data structure using a DList list to store the elements. This is the same class that was provided in the Week 7 Source zip archive. Queue is completed for you. 5.14 Right Paren Represents a right parenthesis in the expression. Righ/Paren is completed for you. 5.15 Stack Implements a generic stack data structure using a DList list to store the elements. This is the same class that was provided in the Module 7 Source zip archive. Stack is completed for you. 5.16 SubOperator Implements the subtraction operator, which is a binary operator. Complete the code in this file by using the Add Operator class as an example. 5.17 Token Token is the abstract superclass of the different types of tokens (i.c., symbols) that can appear in an infix expression. Token is completed for you. 5.18 Tokenizer The Tokenizer class scans a String containing an infix expression and breaks it into tokens. For this project, a token will be either an Operand (a double value), a Left Paren or Right Paren, or an arithmetic UnaryOperator (subclass Neg Operator) or BinaryOperator (one of the AddOperator, Sub Operator, MultOperator, or DivOperator subclasses). Tokenizer is com- pleted for you. It is implemented as a finite state machine (FSM) which are commonly used in computing, especially when breaking a "sentence" of words or symbols into its component parts. If you have the time, you should study the code to learn how FSM's work and are used. Kevin R. Burger: Computer Science & Engineering : Arizona State University :: Rev 26719a Page 5 CSE205 Object Oriented Programming and Data Structures Programming Project 4 :: 25 pts 5.19 Unary Operator Unary Operator is the superclass of all unary operators. Unary Operator is completed for you. 5.20 View The View implements the GUI. Read the comments and implement the pseudocode. 5.21 UML Class Diagram The UML class diagram is provided in the zip archive/url folder as two UMLet files. Because the images in this document are small, there are PNG images of the two class diagrams in the image folder. Your program shall implement this design. + Token(): wtore Operand mValue: Double + Operand(pvalue Double) uctor +qetValue(): Double + setValue(pvalue Double): void Operator + Operator) wctor + is BinaryOperator: boolean precedenceint +StackPrecedence): int 44 Parenthesis +Parenthesis actore +is BinaryOperator() boolean BinaryOperator UnaryOperator +UnaryOperator: ectors evaluate poperard: Operand: Operand + is BinaryOperator'x boolean +Binary Operator(): actor ev alatepthsoperand. Operand, phsoperand: Operand): Operand + is Binary Operator> boolean AAAA Left Paren +LeftParen), wctors + precedence(): int + stackPrecedence int NegOperator + NegOperator): ctor + evaluate Operand: Operand): Operand + precedence(): int + StackPrecedenceint Addoperator + Addoperator): actor + evaluatepths perand: Operand, phsoperand Operand): Operand + precedence(): int + stackPrecedenced in Right Paren +RightParen) wctor + precedence(): int + stackPrecedence int DivOperator + DivOperator): uctor + evaluate puhso perand: Operand, prhso peranch Operand): Operand + precedence(): int + stackPrecedence in Mult Operator + MultOperator): Token Queue -mList: DList +Queuel) actor +clear(); void +dequeue(): E +enqueue(pData: E); void #getuisto: DList +IsEmpty(): boolean peek(): E #setlist(pust: Dust): void +toString(): String Stack -mList: DLISTES +Stack .ctor + clear(); void getList(): DList +isEmpty(): boolean +peek) E +pop(): E +pushpData Ex void setListiplist: DList); void +toString(): String Tokenizer -STATE DOUBLE = 0; final int -STATE ENDl final int -STATE START - 2. final int -mindex: int -mStrings String +Tokenizer pString: String): actor #getindex(int #getString: String + nextToken() Token -nect Char(): Character -peekNext(): Character #setindexpindex: int void #getString(pString: Stringl: vold -ungetChard) void - calls nextToken() Expression -m Tokenqueue: Queue Token + Expression pexprstr String): ector + evaluate(): Double #getTokenQueue). Queues Token -keep Evaluating OperatorstackStack pOperator Operator): boolean -negationCheckipToken: Token pPrevToken: Tokenl: Token #setTokenQueuelpTokenQueue: QueuedToken>void topEval Operator Stack: Stack Operator, poperandStack: Stack Operand); void Kevin R. Burger: Computer Science & Engineering : Arizona State University : Rev 26719a Page 7 CSE205 Object Oriented Programming and Data Structures Programming Project 4 :: 25 pts 6 Additional Project Requirements 1. Format your code neatly. Use proper indentation and spacing. Study the examples in the book and the examples the instructor presents in the lectures and posts on the course website. 2. Put a comment header block at the top of each method formatted thusly: * A brief description of what the method does. */ Put a comment header block at the top of each source code file formatted thusly (or use /** ... */ comments if you wish): //*************** ******************************************************************** 1/ CLASS: classname (classname.java) // COURSE AND PROJECT INFO // CSE205 Object Oriented Programming and Data Structures, semester and year // Project Number: project number // AUTHOR: your name, your-asurite-id, your-email-addr //********* Kevin R. Burger: Computer Science & Engineering :: Arizona State University : Rev 26719a Page 8





![void main(String[] args) { new Main().run(); } /** * exit() is called](https://s3.amazonaws.com/si.experts.images/answers/2024/09/66ddd959c1a4a_12966ddd95932c39.jpg)





