Need help with this and I don't know how to do it!
Please explain full explanations!!!
Calculus stuff such as Derivatives of inverse functions, Implicit Differentiation, Derivatives of Exponential and Logarithmic Functions, Related rates, and L'Hopital's Rule.
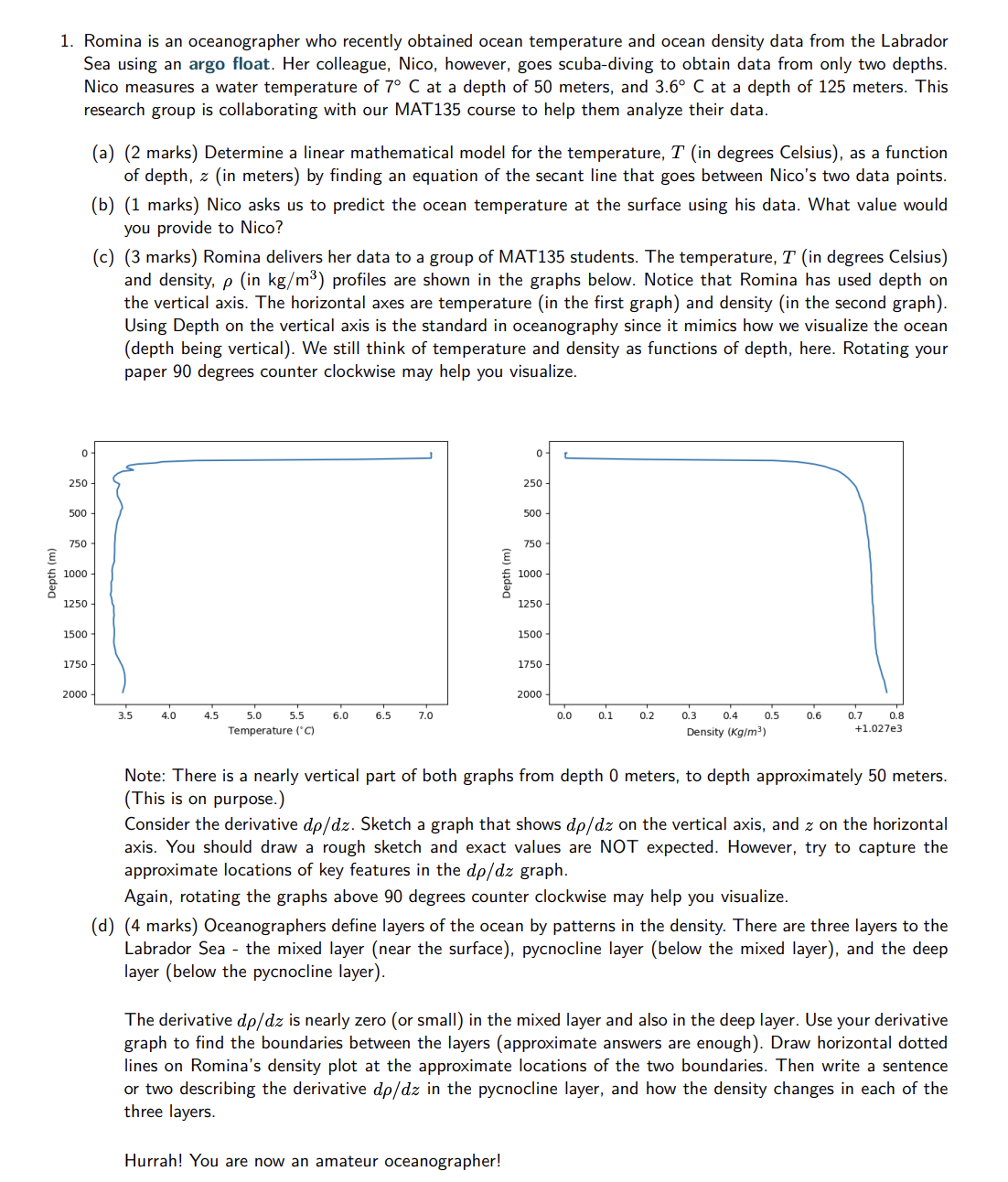
1. Romina is an oceanographer who recently obtained ocean temperature and ocean density data from the Labrador Sea using an argo float. Her colleague, Nico, however, goes scubadiving to obtain data from only two depths. Nico measures a water temperature of 7 C at a depth of 50 meters, and 3.5!" C at a depth of 125 meters. This research group is collaborating with our MAT135 course to help them analyze their data. 250- 500 - 1'50 - 10 00 Depth (m! 12 50 1500 - l? 50 2000 (a) (b) (C) (2 marks) Determine a linear mathematical model for the temperature, T (in degrees Celsius), as a function of depth, 2 (in meters) by nding an equation of the secant line that goes between Nico's two data points. (1 marks) Nico asks us to predict the ocean temperature at the surface using his data. What value would you provide to Nico? (3 marks) Romina delivers her data to a group of MAT135 students. The temperature. T (in degrees Celsius) and density, p (in kg/m3) profiles are shown in the graphs below. Notice that Romina has used depth on the vertical axis. The horizontal axes are temperature (in the first graph) and density (in the second graph). Using Depth on the vertical axis is the standard in oceanography since it mimics how we visualize the ocean (depth being vertical). We still think of temperature and density as functions of depth, here. Rotating your paper 90 degrees counter clockwise may help you visualize. 250 - 500 - 7'50 - 1000 - Depth (In) 1250 - 1500 - l?50 - 2000 - (d) 3.5 4.0 4.5 5.0 5.5 6.0 6.5 10 0. 0 0.1 0.2 0.3 0.4 0.5 0.6 0.? 0.8 Temperaturefcl Density lKgfmll +1.027e3 Note: There is a nearly vertical part of both graphs from depth 0 meters, to depth approximately 50 meters. (This is on purpose.) Consider the derivative tip/dz. Sketch a graph that shows tip/dz on the vertical axis, and z on the horizontal axis. You should draw a rough sketch and exact values are NOT expected. However, try to capture the approximate locations of key features in the tip/dz graph. Again, rotating the graphs above 90 degrees counter clockwise may help you visualize. (4 marks) Oceanographers define layers of the ocean by patterns in the density. There are three layers to the Labrador Sea the mixed layer (near the surface), pycnocline layer (below the mixed layer), and the deep layer (below the pycnocline layer). The derivative tip/dz is nearly zero (or small) in the mixed layer and also in the deep layer. Use your derivative graph to find the boundaries between the layers (approximate answers are enough). Draw horizontal dotted lines on Romina's density plot at the approximate locations of the two boundaries. Then write a sentence or two describing the derivative tip/dz in the pycnocline layer, and how the density changes in each of the three layers. Hurrah! You are now an amateur oceanographer! LEC2*: 1.2 Basic classes of functions LEC3: 1.4 Inverse functions (except inverse trig) LEC4: 1.3 Trigonometry and 1.4 cont. (inverse trig.) LEC5: 1.5 Exponential and logarithmic functions LEC6: 2.1, 2.2 and 2.3 Introduction to limits LEC7: 2.3 cont. LEC8: 2.3 cont. LEC9: 2.4 Continuity LEC10: 2.4 cont. LEC11: 3.1 Defining the derivative LEC12: 3.2 The derivative as a function LEC13: 3.3 Differentiation rules Reading week and Thanks LEC14: 3.3 cont. and 3.4 Deriv. as rates of change LEC15: 3.4 cont. LEC16: Test review (if time) LEC17: 3.5 Derivatives of trigonometric functions LEC18: 3.6 The chain rule LEC19: 3.7 Derivatives of inverse functions LEC20: 3.8 Implicit differentiation LEC21: 3.9 Derivatives of exponential and logarithmic functions LEC22: 4.1 Related rates LEC23: 4.1 cont. and 4.8 L'Hopital's rule LEC24: 4.8 cont