need help with this question

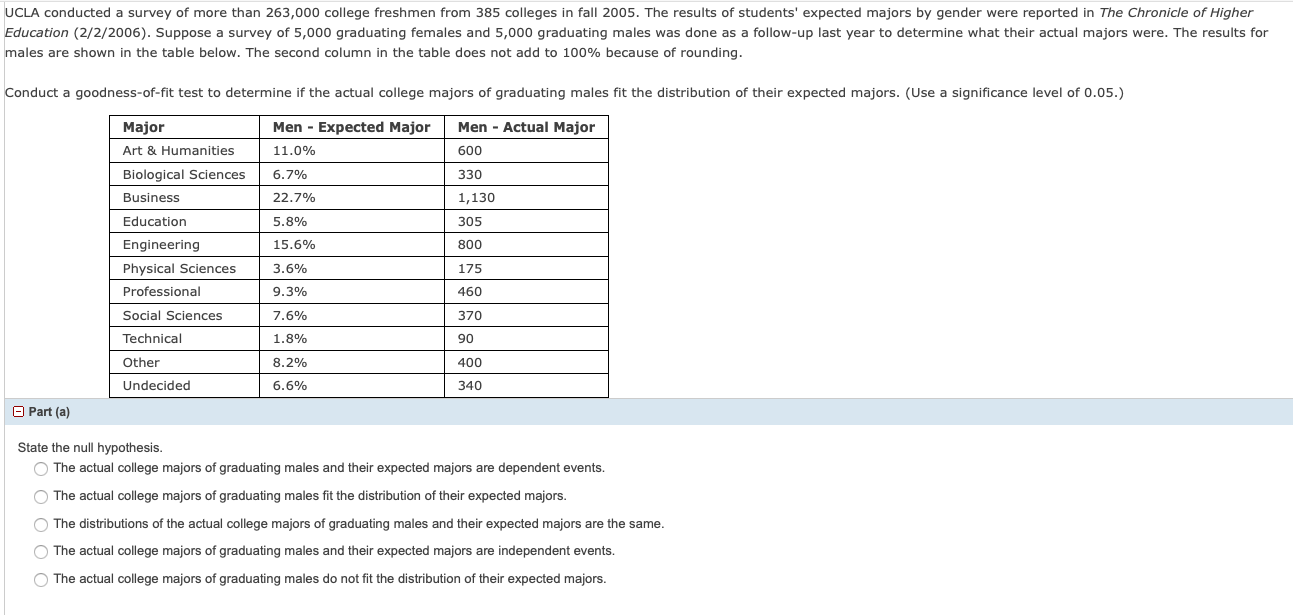
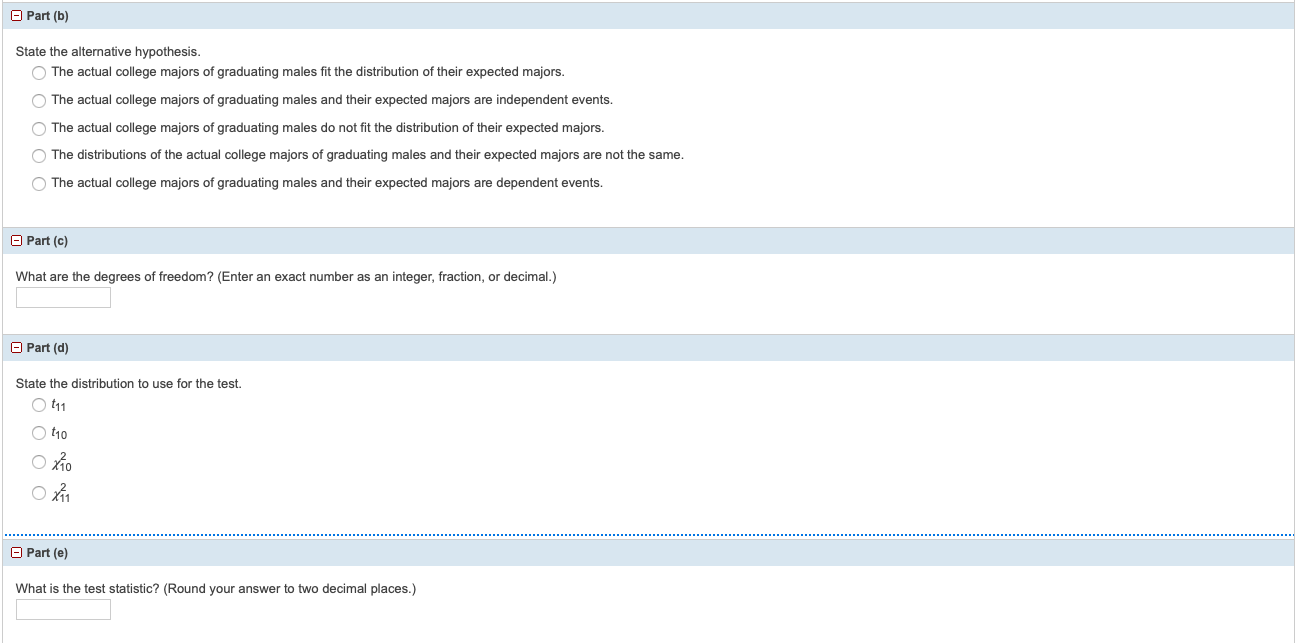
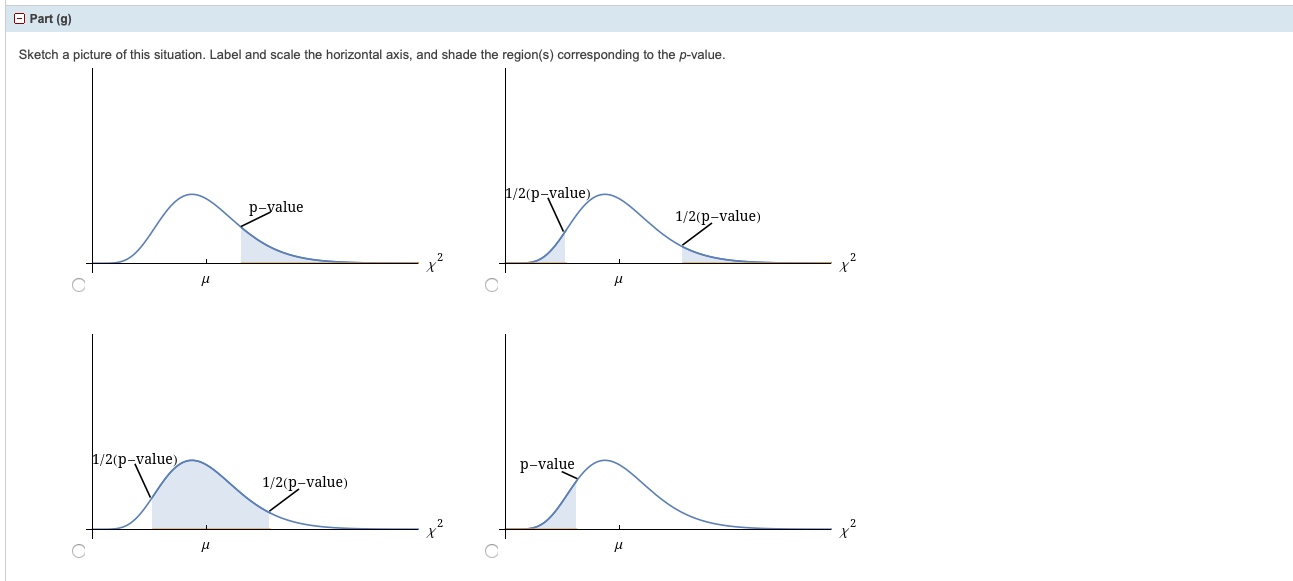
UCLA conducted a survey of more than 263,000 college freshmen from 385 colleges in fall 2005. The results of students' expected majors by gender were reported in The Chronicle of Higher Education (2/2/2006). Suppose a survey of 5,000 graduating females and 5,000 graduating males was done as a follow-up last year to determine what their actual majors were. The results for males are shown in the table below. The second column in the table does not add to 100% because of rounding. Conduct a goodness-of-fit test to determine if the actual college majors of graduating males fit the distribution of their expected majors. (Use a significance level of 0.05.) Major Men - Expected Major Men - Actual Major Art & Humanities 11.0% 500 Biological Sciences 6.7% 330 Business 22.7% 1,130 Education 5.8% 305 Engineering 15.6% 800 Physical Sciences 3.6% 175 Professional 9.3% 460 Social Sciences 7.6% 370 Technical 1.8% 90 Other 8.2% 400 Undecided 6.6% 340 Part (a) State the null hypothesis. O The actual college majors of graduating males and their expected majors are dependent events. The actual college majors of graduating males fit the distribution of their expected majors. The distributions of the actual college majors of graduating males and their expected majors are the same. The actual college majors of graduating males and their expected majors are independent events. The actual college majors of graduating males do not fit the distribution of their expected majors.- Part (b) State the alternative hypothesis. O The actual college majors of graduating males fit the distribution of their expected majors. The actual college majors of graduating males and their expected majors are independent events. The actual college majors of graduating males do not fit the distribution of their expected majors. The distributions of the actual college majors of graduating males and their expected majors are not the same. The actual college majors of graduating males and their expected majors are dependent events. Part (c) What are the degrees of freedom? (Enter an exact number as an integer, fraction, or decimal.) Part (d) State the distribution to use for the test. O t11 O t10 O X10 Part (e) What is the test statistic? (Round your answer to two decimal places.)B Part [1) What is the pvalue? Q p-velue 11100 Explain what lhe pvalue means for this problem. 0 If Ho false. then Ihere is a chance equal In the pvalue Ihat the value ofthe teen 513115115 will be equal [0 or greater than the calwlaled value. 0 If H0 is false, then Ihere is a chance equal In the pvalue 11181 the value ofthe teen 513115115 will be equal to or less than the calculaled value. 0 If Ho "a true, then there is a chance equal In the pvalue that the value of the test statistic will be equal In or leg than the nalmlated value. 0 If Hg is true. than there is a chance equal to the pvalue that the value of the test statistic will be equal to or greater than the calwlated value. - Part (9) Sketch a picture of this situation. Label and scale the horizontal axis, and shade the region(s) corresponding to the p-value. 1/2(p-value) p-value 1/2(p-value) 2 H C 1/2(p-value) p-value 1/2(p-value) 2 X H- Part (h) Indicate the correct decision ("reject" or "do not reject" the null hypothesis), the reason for it, and write the appropriate conclusion. (i) Alpha (Enter an exact number as an integer, fraction, or decimal.) of = (ii) Decision: reject the null hypothesis O do not reject the null hypothesis (ii) Reason for decision: Since a p-value, we reject the null hypothesis. Since a p-value, we do not reject the null hypothesis. (iv) Conclusion: O There is sufficient evidence to conclude that the distribution of actual college majors of graduating males do not fit the distribution of their expected majors. There is not sufficient evidence to conclude that the distribution of actual college majors of graduating males do not fit the distribution of their expected majors