Question: Need in JAVA please and thanks! need asap if possible.. 1. Create a new Eclipse project and within it create a package hw2. Create the
Need in JAVA please and thanks! need asap if possible..
1. Create a new Eclipse project and within it create a package hw2. Create the Padlock class in the hw1 package and put in stubs for all the required methods, the constructor, and the required constant. Remember that everything listed is declared public. For methods that are required to return a value, just put in a "dummy" return statement that returns zero. There should be no compile errors. You should be able to run the sample main class SimpleTest.java.
2. Briefly javadoc the class, constructor and methods. This is a required part of the assignment anyway, and doing it now will help clarify for you what each method is supposed to do before you begin the actual implementation. (Copying from the method descriptions here or in the Javadoc is perfectly acceptable; however, DO NOT COPY AND PASTE DIRECTLY from the pdf or online Javadoc! This leads to insidious bugs caused by invisible characters that are sometimes generated by sophisticated document formats. If you are super lazy about typing, it should be ok if you copy, paste into a dumb text editor like Notepad, and then copy/paste from there.)
3. You could start by first making sure you can set and get the current rotation of each disc. According to the constructor, assuming that the tooth width is 2 degrees, the initial position of the discs is always 0 degrees for disc 3, 2 degrees for disc 2, and 4 degrees for disc 1. (This is true regardless of the constructor arguments.). So you should be able to set up a simple test class with the following: Padlock p = new Padlock(10, 20, 30); printPositions(p); // expected 4 2 0 p.setPositions(42, 137, 17); // order is disc 1, 2, 3 printPositions(p); // expected 42 137 17 where printPositions is a helper method that just uses the getDiscPosition method to display the three angles: private static void printPositions(Padlock p) { int c = p.getDiscPosition(3); int b = p.getDiscPosition(2); int a = p.getDiscPosition(1); System.out.println(a + " " + b + " " + c); // back to front (1, 2, 3) } This would also be a good time to make sure you can normalize the angles so they are always between 0 and 359, for example: p.setPositions(-90, 800, 42); printPositions(p); // expected 270 80 42 (Tip: the sample code shown above can be found in the given file SimpleTest.java)
3. At this point you could either continue working on disc rotations, or implement the lock logic; the two tasks can be tackled independently. Suppose we do lock logic first. The key piece is determining whether the discs are "aligned", as specified in the isAligned method. For that we need to know the offset for each disc, that is, the angle of rotation that will put its notch in the right position for the lock to open. According to the general description of the lock internals, if the combination is 10, 20, 30, then the offsets are 6, 22, and 30, for discs 1, 2, and 3, respectively. The isAligned method should return true if the current positions of all three discs match their offsets. So, the behavior we expect is something like this (according to the constructor, the lock should initially be open): System.out.println(p.isOpen()); // expected true System.out.println(p.isAligned()); // expected false p.close(); System.out.println(p.isOpen()); // expected false p.open(); // does nothing; it's locked System.out.println(p.isOpen()); // expected false p.setPositions(6, 22, 30); printPositions(p); // expected 6, 22, 30 System.out.println(p.isAligned()); // expected true // now we should be able to open it! p.open(); System.out.println(p.isOpen()); // expected true System.out.println();
4. To start thinking about what happens when you rotate the dial, first think about just disc 3, the front one that is attached to the dial. You could start by just making sure you can get disc 3 to end up in the correct position: p.setPositions(4, 2, 0); p.turn(10); // 10 degrees ccw System.out.println(p.getDiscPosition(3)); // expected 10 p.turn(-100); // 100 degrees cw System.out.println(p.getDiscPosition(3)); // expected 270 p.turn(800); System.out.println(p.getDiscPosition(3)); // expected 350 System.out.println();
5. Now it gets interesting. How does disc 3 affect disc 2? Suppose disc 3 is at 30 degrees and disc 2 is at 90 degrees, and we rotate disc 3 counterclockwise (ccw) 70 degrees. p.setPositions(0, 90, 30); p.turn(70); printPositions(p); // expected 0 102 100 Here, (disc 2 position) (disc 3 position) = 90 30 = 60 degrees, the counterclockwise rotation from disc 3 to disc 2. There is also the tooth width to account for, so disc 3 can rotate 58 degrees before it starts pushing disc 2. We're rotating disc 3 a total of 70 degrees ccw, so disc 2 will be pushed 12 degrees ccw, ending up at position 102. Maybe we should try one where the subtraction comes out negative: p.setPositions(0, 20, 350); p.turn(50); printPositions(p); // expected 0 42 40 In this case, (disc 2 position) (disc 3 position) = -330 degrees, which normalizes to 30 degrees. With the tooth width, disc 3 can rotate 28 degrees ccw before affecting disc 2. We're rotating 50 degrees, so disc 2 is pushed 22 degrees.
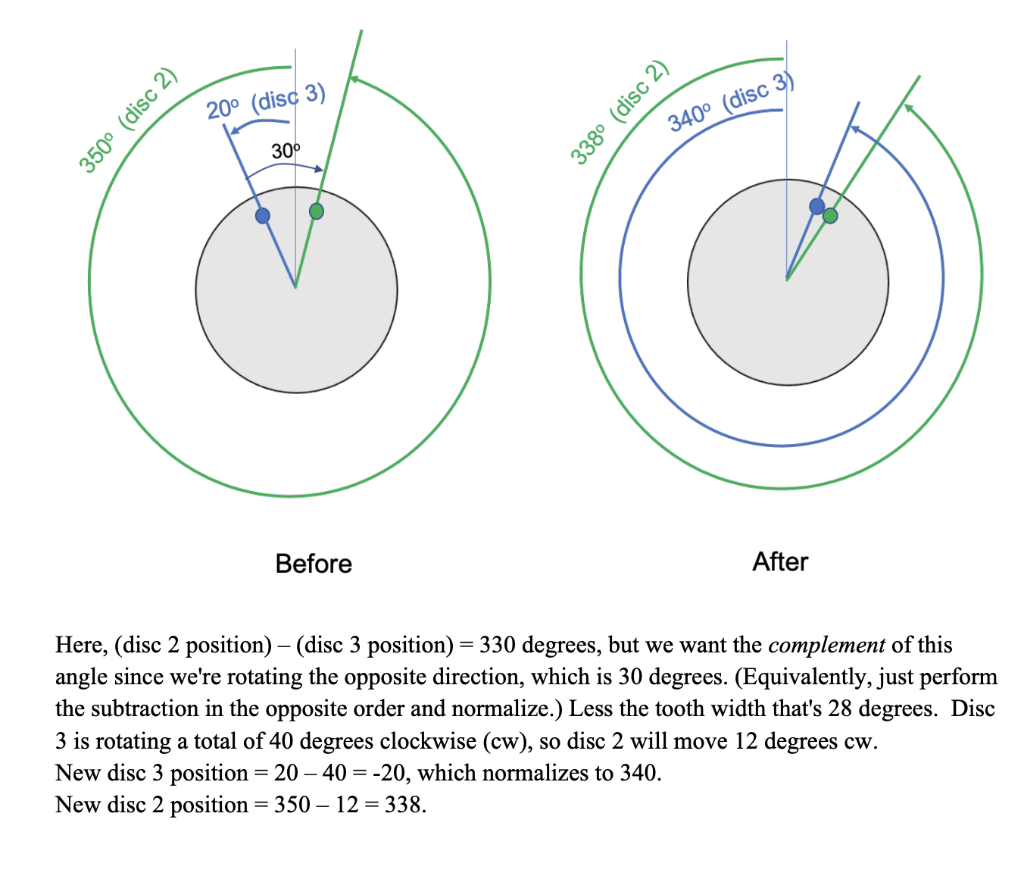
6. Then try going clockwise: p.setPositions(0, 350, 20); p.turn(-40); printPositions(p); // expected 0 338 340 Here, (disc 2 position) (disc 3 position) = 330 degrees, but we want the complement of this angle since we're rotating the opposite direction, which is 30 degrees. (Equivalently, just perform the subtraction in the opposite order and normalize.) Less the tooth width that's 28 degrees. Disc 3 is rotating a total of 40 degrees clockwise (cw), so disc 2 will move 12 degrees cw. New disc 3 position = 20 40 = -20, which normalizes to 340. New disc 2 position = 350 12 = 338. Try another one: p.setPositions(45, 40, 30); p.turn(-400); printPositions(p); // expected 45 348 350 Here, (disc 2 position) (disc 3 position) = 10 degrees, but we want the complement of this angle since we're rotating the opposite direction, which is 350 degrees; less the tooth width that's 348 degrees. Disc 1 is rotating 400 degrees cw, so disc 2 will be pushed 52 degrees. New disc 3 position = 30 400 = -370, which normalizes to 350. New disc 2 position = 40 52 = -12, which normalizes to 348. Accounting for the effect of disc 2 on disc 1 is similar. In the test case above, for example, we can tell that the difference, (disc 1 position) (disc 2 position) = 45 - 40 = 5 degrees, the complement of which is 355, less the tooth width is 353; but disc 2 is only rotating 52 degrees cw, so disc 1 is unaffected. If we instead had the same example but with disc 1 at 10 degrees: p.setPositions(10, 40, 30); p.turn(-400); printPositions(p); // expected 346 348 350 Now, (disc 1 position) (disc 2 position) = -30 degrees, normalized to 330, but we want the complement which is 30, and allowing for the tooth width, we get 28 degrees cw from disc 2 to disc 1. Disc 2 is moving 52 degrees cw as in previous example, so disc 1 will be pushed 24 degrees cw. New disc 1 position is 10 24 = -14 or 346 degrees.
7. Once turn is implemented, it is easy to implement the methods turnLeftTo and turnRightTo. After that, you should be able to open the lock according the instructions on the package (recall we originally constructed a padlock with combination 10, 20, 30): p.turn(-720); // spin it twice clockwise p.turnRightTo(10); p.turn(360 - Padlock.TOOTH); // counterclockwise a full revolution p.turnLeftTo(20); p.turnRightTo(30); System.out.println(p.isAligned()); // expected true p.open(); System.out.println(p.isOpen()); // hooray







1. Create a new Eclipse project and within it create a package hw2. Create the Padlock class in the hwl package and put in stubs for all the required methods, the constructor, and the required constant. Remember that everything listed is declared public. For methods that are required to return a value, just put in a "dummy" return statement that returns zero. There should be no compile errors. You should be able to run the sample main class SimpleTest.java. 2. Briefly javadoc the class, constructor and methods. This is a required part of the assignment anyway, and doing it now will help clarify for you what each method is supposed to do before you begin the actual implementation. (Copying from the method descriptions here or in the Javadoc is perfectly acceptable; however, DO NOT COPY AND PASTE DIRECTLY from the pdf or online Javadoc! This leads to insidious bugs caused by invisible characters that are sometimes generated by sophisticated document formats. If you are super lazy about typing, it should be ok if you copy, paste into a dumb text editor like Notepad, and then copy/paste from there.) 3. You could start by first making sure you can set and get the current rotation of each disc. According to the constructor, assuming that the tooth width is 2 degrees, the initial position of the discs is always 0 degrees for disc 3, 2 degrees for disc 2, and 4 degrees for disc 1. (This is true regardless of the constructor arguments.). So you should be able to set up a simple test class with the following: Padlock p = new Padlock (10, 20, 30); printPositions (p); p.setPositions (42, 137, 17); printPositions (p); // expected 4 20 11 order is disc 1, 2, 3 // expected 42 137 17 where printPositions is a helper method that just uses the getDiscPosition method to display the three angles: private static void printPositions (Padlock p) { int c = p.getDiscPosition (3); int b = p.getDiscPosition (2); int a = p.getDiscPosition (1); System.out.println(a + " " + b + " " + c); } // back to front (1, 2, 3) This would also be a good time to make sure you can normalize the angles so they are always between 0 and 359, for example: p.setPositions (-90, 800, 42); printPositions (p); // expected 270 80 42 (Tip: the sample code shown above can be found in the given file SimpleTest.java) 3. At this point you could either continue working on disc rotations, or implement the lock logic; the two tasks can be tackled independently. Suppose we do lock logic first. The key piece is determining whether the discs are "aligned", as specified in the isAligned method. For that we need to know the offset for each disc, that is, the angle of rotation that will put its notch in the right position for the lock to open. According to the general description of the lock internals, if the combination is 10, 20, 30, then the offsets are 6, 22, and 30, for discs 1, 2, and 3, respectively. The isAligned method should return true if the current positions of all three discs match their offsets. So, the behavior we expect is something like this (according to the constructor, the lock should initially be open): 1/ expected true 1/ expected false System.out.println(p.isOpen()); System.out.println(p.isAligned()); p.close(); System.out.println(p.isOpen()); p.open(); System.out.println(p.isOpen()); p.setPositions (6, 22, 30); printPositions (p); System.out.println(p.isAligned()); // expected false 1/ does nothing; it's locked 1/ expected false 1/ expected 6, 22, 30 1/ expected true // now we should be able to open it! p.open(); System.out.println(p.isOpen()); System.out.println(); 1/ expected true 4. To start thinking about what happens when you rotate the dial, first think about just disc 3, the front one that is attached to the dial. You could start by just making sure you can get disc 3 to end up in the correct position: p.setPositions (4, 2, 0); p. turn (10); // 10 degrees CCW System.out.println(p.getDiscPosition (3) ); // expected 10 p. turn(-100); // 100 degrees Cw System.out.println(p.getDiscPosition (3)); // expected 270 p. turn (800); System.out.println(p.getDiscPosition (3)); // expected 350 System.out.println(); 5. Now it gets interesting. How does disc 3 affect disc 2? Suppose disc 3 is at 30 degrees and disc 2 is at 90 degrees, and we rotate disc 3 counterclockwise (ccw) 70 degrees. p.setPositions (0, 90, 30); p. turn (70); printPositions (p); // expected 0 102 100 90 (disc 2) 30 (disc 3) 600 102 (disc 2) 100 (disc 3) 58 Disc 3 tooth o Disc 2 tooth Before After Here, (disc 2 position) (disc 3 position) = 90 30 = 60 degrees, the counterclockwise rotation from disc 3 to disc 2. There is also the tooth width to account for, so disc 3 can rotate 58 degrees before it starts pushing disc 2. We're rotating disc 3 a total of 70 degrees ccw, so disc 2 will be pushed 12 degrees ccw, ending up at position 102. Maybe we should try one where the subtraction comes out negative: p.setPositions (0, 20, 350); p. turn (50); printPositions (p); // expected 0 42 40 In this case, (disc 2 position) (disc 3 position) = -330 degrees, which normalizes to 30 degrees. With the tooth width, disc 3 can rotate 28 degrees ccw before affecting disc 2. We're rotating 50 degrees, so disc 2 is pushed 22 degrees. 6. Then try going clockwise: p.setPositions (0, 350, 20); p. turn(-40); printPositions (p); // expected 0 338 340 20 (disc 3) 350 (disc 2) 338 (disc 2) 340 (disc 3) 300 Before After Here, (disc 2 position) (disc 3 position) = 330 degrees, but we want the complement of this angle since we're rotating the opposite direction, which is 30 degrees. (Equivalently, just perform the subtraction in the opposite order and normalize.) Less the tooth width that's 28 degrees. Disc 3 is rotating a total of 40 degrees clockwise (cw), so disc 2 will move 12 degrees cw. New disc 3 position = 20 40 = -20, which normalizes to 340. New disc 2 position = 350 12 = 338. Try another one: p.setPositions (45, 40, 30); p. turn (-400); printPositions (p); // expected 45 348 350 Here, (disc 2 position) (disc 3 position) = 10 degrees, but we want the complement of this angle since we're rotating the opposite direction, which is 350 degrees; less the tooth width that's 348 degrees. Disc 1 is rotating 400 degrees cw, so disc 2 will be pushed 52 degrees. New disc 3 position = 30 400 = -370, which normalizes to 350. New disc 2 position = 40 52 =-12, which normalizes to 348. Accounting for the effect of disc 2 on disc 1 is similar. In the test case above, for example, we can tell that the difference, (disc 1 position) (disc 2 position) = 45 - 40 = 5 degrees, the complement of which is 355, less the tooth width is 353; but disc 2 is only rotating 52 degrees cw, so disc 1 is unaffected. If we instead had the same example but with disc 1 at 10 degrees: p.setPositions (10, 40, 30); p. turn (-400); printPositions (p); // expected 346 348 350 Now, (disc 1 position) (disc 2 position) = -30 degrees, normalized to 330, but we want the complement which is 30, and allowing for the tooth width, we get 28 degrees cw from disc 2 to disc 1. Disc 2 is moving 52 degrees cw as in previous example, so disc 1 will be pushed 24 degrees cw. New disc 1 position is 10 24 =-14 or 346 degrees. 7. Once turn is implemented, it is easy to implement the methods turnLeftTo and turnRightto. After that, you should be able to open the lock according the instructions on the package (recall we originally constructed a padlock with combination 10, 20, 30): 7. Once turn is implemented, it is easy to implement the methods turnLeftto and turnRightTo. After that, you should be able to open the lock according the instructions on the package (recall we originally constructed a padlock with combination 10, 20, 30): p. turn(-720); // spin it twice clockwise p. turnRightTo(10); p. turn(360 - Padlock. TOOTH) ; // counterclockwise a full revolution p. turnLeftTo(20); p. turnRightTo (30); System.out.println(p.isAligned()); // expected true p.open(); System.out.println(p.isOpen()); // hooray 1. Create a new Eclipse project and within it create a package hw2. Create the Padlock class in the hwl package and put in stubs for all the required methods, the constructor, and the required constant. Remember that everything listed is declared public. For methods that are required to return a value, just put in a "dummy" return statement that returns zero. There should be no compile errors. You should be able to run the sample main class SimpleTest.java. 2. Briefly javadoc the class, constructor and methods. This is a required part of the assignment anyway, and doing it now will help clarify for you what each method is supposed to do before you begin the actual implementation. (Copying from the method descriptions here or in the Javadoc is perfectly acceptable; however, DO NOT COPY AND PASTE DIRECTLY from the pdf or online Javadoc! This leads to insidious bugs caused by invisible characters that are sometimes generated by sophisticated document formats. If you are super lazy about typing, it should be ok if you copy, paste into a dumb text editor like Notepad, and then copy/paste from there.) 3. You could start by first making sure you can set and get the current rotation of each disc. According to the constructor, assuming that the tooth width is 2 degrees, the initial position of the discs is always 0 degrees for disc 3, 2 degrees for disc 2, and 4 degrees for disc 1. (This is true regardless of the constructor arguments.). So you should be able to set up a simple test class with the following: Padlock p = new Padlock (10, 20, 30); printPositions (p); p.setPositions (42, 137, 17); printPositions (p); // expected 4 20 11 order is disc 1, 2, 3 // expected 42 137 17 where printPositions is a helper method that just uses the getDiscPosition method to display the three angles: private static void printPositions (Padlock p) { int c = p.getDiscPosition (3); int b = p.getDiscPosition (2); int a = p.getDiscPosition (1); System.out.println(a + " " + b + " " + c); } // back to front (1, 2, 3) This would also be a good time to make sure you can normalize the angles so they are always between 0 and 359, for example: p.setPositions (-90, 800, 42); printPositions (p); // expected 270 80 42 (Tip: the sample code shown above can be found in the given file SimpleTest.java) 3. At this point you could either continue working on disc rotations, or implement the lock logic; the two tasks can be tackled independently. Suppose we do lock logic first. The key piece is determining whether the discs are "aligned", as specified in the isAligned method. For that we need to know the offset for each disc, that is, the angle of rotation that will put its notch in the right position for the lock to open. According to the general description of the lock internals, if the combination is 10, 20, 30, then the offsets are 6, 22, and 30, for discs 1, 2, and 3, respectively. The isAligned method should return true if the current positions of all three discs match their offsets. So, the behavior we expect is something like this (according to the constructor, the lock should initially be open): 1/ expected true 1/ expected false System.out.println(p.isOpen()); System.out.println(p.isAligned()); p.close(); System.out.println(p.isOpen()); p.open(); System.out.println(p.isOpen()); p.setPositions (6, 22, 30); printPositions (p); System.out.println(p.isAligned()); // expected false 1/ does nothing; it's locked 1/ expected false 1/ expected 6, 22, 30 1/ expected true // now we should be able to open it! p.open(); System.out.println(p.isOpen()); System.out.println(); 1/ expected true 4. To start thinking about what happens when you rotate the dial, first think about just disc 3, the front one that is attached to the dial. You could start by just making sure you can get disc 3 to end up in the correct position: p.setPositions (4, 2, 0); p. turn (10); // 10 degrees CCW System.out.println(p.getDiscPosition (3) ); // expected 10 p. turn(-100); // 100 degrees Cw System.out.println(p.getDiscPosition (3)); // expected 270 p. turn (800); System.out.println(p.getDiscPosition (3)); // expected 350 System.out.println(); 5. Now it gets interesting. How does disc 3 affect disc 2? Suppose disc 3 is at 30 degrees and disc 2 is at 90 degrees, and we rotate disc 3 counterclockwise (ccw) 70 degrees. p.setPositions (0, 90, 30); p. turn (70); printPositions (p); // expected 0 102 100 90 (disc 2) 30 (disc 3) 600 102 (disc 2) 100 (disc 3) 58 Disc 3 tooth o Disc 2 tooth Before After Here, (disc 2 position) (disc 3 position) = 90 30 = 60 degrees, the counterclockwise rotation from disc 3 to disc 2. There is also the tooth width to account for, so disc 3 can rotate 58 degrees before it starts pushing disc 2. We're rotating disc 3 a total of 70 degrees ccw, so disc 2 will be pushed 12 degrees ccw, ending up at position 102. Maybe we should try one where the subtraction comes out negative: p.setPositions (0, 20, 350); p. turn (50); printPositions (p); // expected 0 42 40 In this case, (disc 2 position) (disc 3 position) = -330 degrees, which normalizes to 30 degrees. With the tooth width, disc 3 can rotate 28 degrees ccw before affecting disc 2. We're rotating 50 degrees, so disc 2 is pushed 22 degrees. 6. Then try going clockwise: p.setPositions (0, 350, 20); p. turn(-40); printPositions (p); // expected 0 338 340 20 (disc 3) 350 (disc 2) 338 (disc 2) 340 (disc 3) 300 Before After Here, (disc 2 position) (disc 3 position) = 330 degrees, but we want the complement of this angle since we're rotating the opposite direction, which is 30 degrees. (Equivalently, just perform the subtraction in the opposite order and normalize.) Less the tooth width that's 28 degrees. Disc 3 is rotating a total of 40 degrees clockwise (cw), so disc 2 will move 12 degrees cw. New disc 3 position = 20 40 = -20, which normalizes to 340. New disc 2 position = 350 12 = 338. Try another one: p.setPositions (45, 40, 30); p. turn (-400); printPositions (p); // expected 45 348 350 Here, (disc 2 position) (disc 3 position) = 10 degrees, but we want the complement of this angle since we're rotating the opposite direction, which is 350 degrees; less the tooth width that's 348 degrees. Disc 1 is rotating 400 degrees cw, so disc 2 will be pushed 52 degrees. New disc 3 position = 30 400 = -370, which normalizes to 350. New disc 2 position = 40 52 =-12, which normalizes to 348. Accounting for the effect of disc 2 on disc 1 is similar. In the test case above, for example, we can tell that the difference, (disc 1 position) (disc 2 position) = 45 - 40 = 5 degrees, the complement of which is 355, less the tooth width is 353; but disc 2 is only rotating 52 degrees cw, so disc 1 is unaffected. If we instead had the same example but with disc 1 at 10 degrees: p.setPositions (10, 40, 30); p. turn (-400); printPositions (p); // expected 346 348 350 Now, (disc 1 position) (disc 2 position) = -30 degrees, normalized to 330, but we want the complement which is 30, and allowing for the tooth width, we get 28 degrees cw from disc 2 to disc 1. Disc 2 is moving 52 degrees cw as in previous example, so disc 1 will be pushed 24 degrees cw. New disc 1 position is 10 24 =-14 or 346 degrees. 7. Once turn is implemented, it is easy to implement the methods turnLeftTo and turnRightto. After that, you should be able to open the lock according the instructions on the package (recall we originally constructed a padlock with combination 10, 20, 30): 7. Once turn is implemented, it is easy to implement the methods turnLeftto and turnRightTo. After that, you should be able to open the lock according the instructions on the package (recall we originally constructed a padlock with combination 10, 20, 30): p. turn(-720); // spin it twice clockwise p. turnRightTo(10); p. turn(360 - Padlock. TOOTH) ; // counterclockwise a full revolution p. turnLeftTo(20); p. turnRightTo (30); System.out.println(p.isAligned()); // expected true p.open(); System.out.println(p.isOpen()); // hooray
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


