Need wolfram and MATLAB solution of whole question.

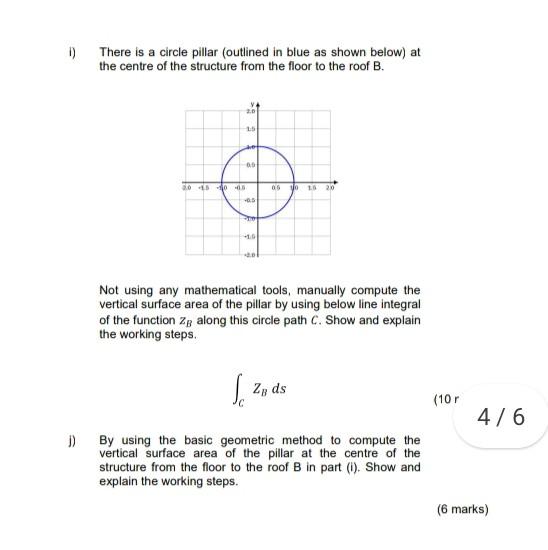
1. There are two types of roof of a rectangular floor (24m x 20m) base structure. Roof A could be modelled by 1 21(x, y) = 3+ (x3 - 144x) + 1000 1 Rood B could be modelled by 2/6 28(x, y) = 5- 1 (x2 + y2) 100 (x,y) is the coordinate of the floor with (0,0) as the coordinate of the centre of the floor, i.e. x = -12 to 12, y = -10 to 10. Use the online mathematical tools Wolfram Alpha to compute below (a), (b), (d), (e) and (h). Use Matlab (integral2 function) to compute below (f) and (g). Show and explain the working steps, particularly on how the upper and lower limits are obtained for (d), (e)and (i), together with the screen captures in your solutions. a) Use Wolfram Alpha to show the 3D graph of the roof A (i.e. function zA) above the floor region - 12 SX S12 and -10 Sy s 10. (2 marks) b) Use Wolfram Alpha to calculate the volume of the structure with roof A by using both double integrals. z(x,y) S\D%26.9)dx]dy = LS*206.9) dx dy 1' [D*26*.9 ) dy]dx = D. D*26*. ) dy dx z(x,y) = xy (4 marks) Page 2 of 7 c) Not using any mathematical tools, manually compute the volume of the structure with roof A by using below double integrals. S S%2.dx]dy = S S%2C%. (xy = z(x,y) dx dy (8 marks) d) There is a parabola + rectangular pillar (outlined in blue as shown below) at the centre of the structure from the floor to the roof A. 1 Parabola y2 = ax + b Find the volume of the pillar by using below double integrals via Wolfram Alpha. Show and explain the working steps, particularly on how the upper and lower limits are obtained. CHOy) z(x,y) dx dy (15 marks) Page 3 of 7 e) By using the reversed order double integrals, find the volume of the pillar in part (d) at the centre of the structure from the floor to the roof A via Wolfram Alpha. Show and explain the working steps, particularly on how the upper and lower limits are obtained. GX 2(x,y) dy dx g(x) (15 marks) f) Use Matlab (integral2 function) to find the volume of the pillar in (d) at the centre of the structure from the floor to the roof A by using below double integrals. Use the limits that you have found in (d). Hy) z(x,y) dx dy (8 marks) g) Use Matlab (integral2 function) to find the volume of the pillar in (d) at the centre of the structure from the floor to the roof A by using the reversed order double integrals. Use the limits that you have found in (e). S. G(X) z(x,y) dy dx g(x) (10 marks) D) There is a circle pillar (outlined in blue as shown below) at the centre of the structure from the floor to the roof B. 15 05 06 Vo 13 20 2050-13 -0.5 Not using any mathematical tools, manually compute the vertical surface area of the pillar by using below line integral of the function Zg along this circle path C. Show and explain the working steps. Je zu ds (107 4/6 1) By using the basic geometric method to compute the vertical surface area of the pillar at the centre of the structure from the floor to the roof B in part (). Show and explain the working steps. (6 marks)