


Need Your help with this activities/lesson, ill surely give you FEEDBACK/thumbsup.
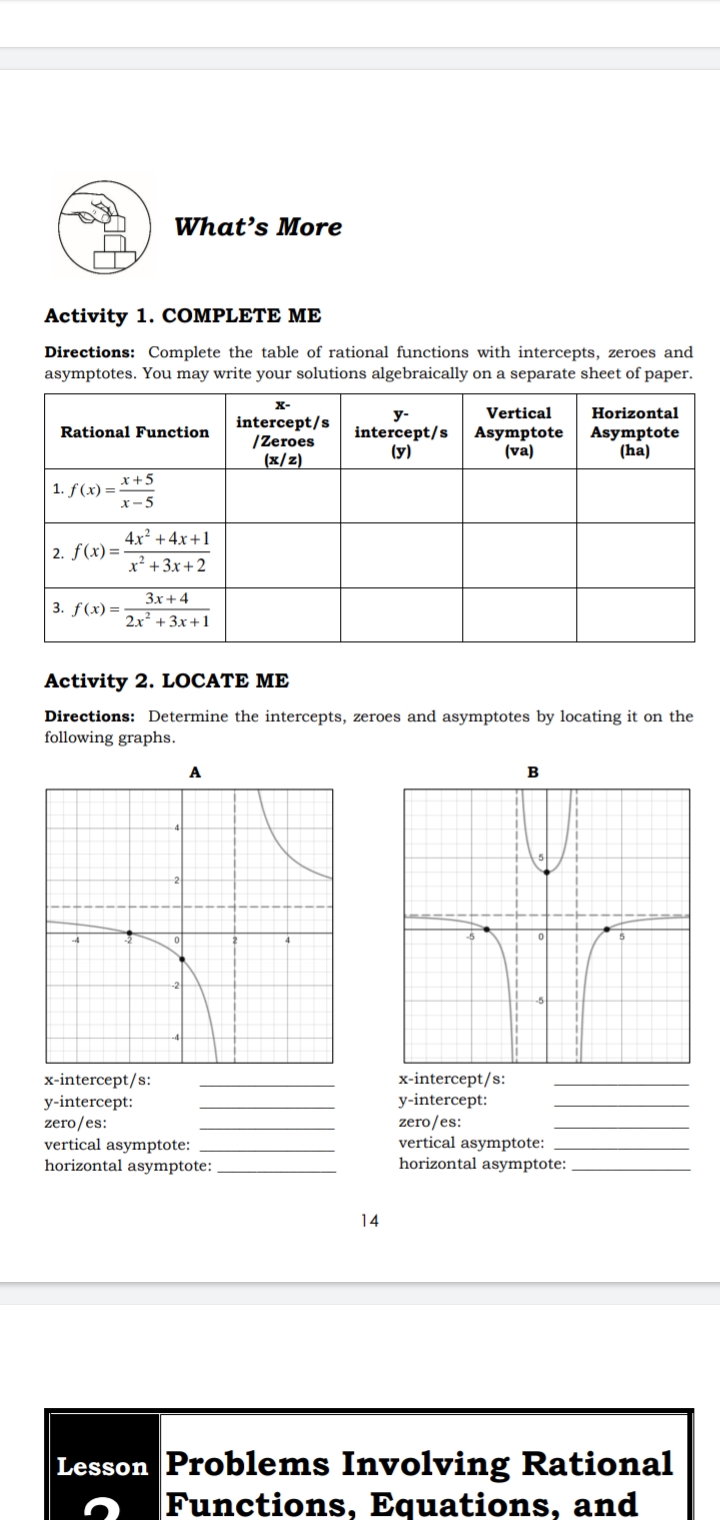
What's More Activity 1. COMPLETE ME Directions: Complete the table of rational functions with intercepts, zeroes and asymptotes. You may write your solutions algebraically on a separate sheet of paper. X- intercept/s y- Vertical Horizontal Rational Function /Zeroes intercept/s Asymptote Asymptote (x/ z) (y) (va) (ha) 1. f (x ) = : _x+5 x-5 4x- +4x +1 2. f ( x) = - x2 + 3x+2 3. f (x) = 3x + 4 2x3 + 3x+1 Activity 2. LOCATE ME Directions: Determine the intercepts, zeroes and asymptotes by locating it on the following graphs. B x-intercept/s: x-intercept/s: y-intercept: y-intercept: zero/ es: zero/ es: vertical asymptote: vertical asymptote: horizontal asymptote: horizontal asymptote: 14 Lesson Problems Involving Rational Functions, Equations, andFor the horizontal asymptote, we have, y = = = 3. Since the x and y intercepts are already in the left region, we won't need to get any points there. That means, we'll just get a point in the right region. Say, x = 2. 2-1 f(2) = (2)+6 - 12 = 12 (2,12) Plotting these points on the graph, we get the following. The definition of rational equations, inequalities and functions are summarized below. Rational Equation Rational Inequality Rational Function Definition An equation involving An inequality involving A function of the form rational expressions. rational expressions. q(x) f(x) = 2 where p(x) and q (x) are polynomial functions and q(x) is a nonzero function (Le., q(x) = 0). Example 2_3 1 X 2x #5 f(x) = *' + 2x +3 x+1 18 A rational equation or inequality can be solved for all x values that satisfy the equation or inequality. Whereas we solve an equation or inequality, we do not "solve" functions. Rather, a function (and in particular, a rational function) expresses a relationship between two variables (such as x and y), and can be represented by a table of values or a graph. Activity 3. Determine whether the given is a rational function, rational equation, rational inequality, or none of these. 1. y = 5x3 - 2x + 1 1 = x3 x+1 2. 9 - 8 = 7 5. g(x) = 2x-4x+1 x2+3 3. Vx - 2 =4 6. 6x - - 20 x+3 Activity 4. Find the solutions for each rational equation below. Make sure to check for extraneous solutions. 1. 4. X-4x _14-9x x+1 x-2 x-2 -2 = 2 2 7+1 2x 5. 2x-1 - = 5 x+3 3. x2-10 -14-5x x-1 x-1 Activity 5. Find the solution set for each rational inequality below. Graph the solution set on a number line. 1. (x+3)(x-2) > 0 4. x-2 (x+2)(x-1) x2-3x-10 - too ). 5. There are three possibilities in determining horizontal asymptote(s) of a rational function. . If n m, horizontal asymptote. 6. A is an expression that can be written as a ratio of two polynomials. 7. A is an inequality involving rational expressions. 8. is a function of the form f(x) = P2 Where p(x)and q(x) are polynomial functions and q(x) is a nonzero polynomial 9. A is an equation containing at least one ratio of two polynomials. 10. To solve a rational equation, eliminate denominators by multiplying each term of the equation by the What I Can Do Rational functions abound in real life, we just don't always think of them that way. Read and understand the problem carefully. Suppose you are buying face mask for yourself, your friends, and family during this Covid-19 pandemic. The face mask shop has a deal going, if you buy one facemask for 35 pesos, then additional face masks are only 30 pesos each. As you buy more and more face masks (more and more as the health risk arise!), what is the average cost per face mask? Represent this situation into a rational equation showing the price per face mask based on number purchased, and the number of face masks. Determine its horizontal asymptotes and explain what this represents. 20 / 25 20 AssessmentAdditional Activities This section mcludes supplementary activities related to rational functions, equations and inequalities. 1. Give examples of problems or situations in real life that involve the use of rational equation, inequality, and function. In each example, a. explain the problem or situation. b. solve the problem. discuss how you can use these sample situations in your daily life, especially in formulating conclusions and! or making decisions 512 1:2 +7 intercepts. zeroes and horizontal asymptote. 2. Show that fix} = has no vertical asymptote algebraically. Determine its 22














