NetMath UIUC Lesson 2 Try It 2

Question 4.a-4.d.ii

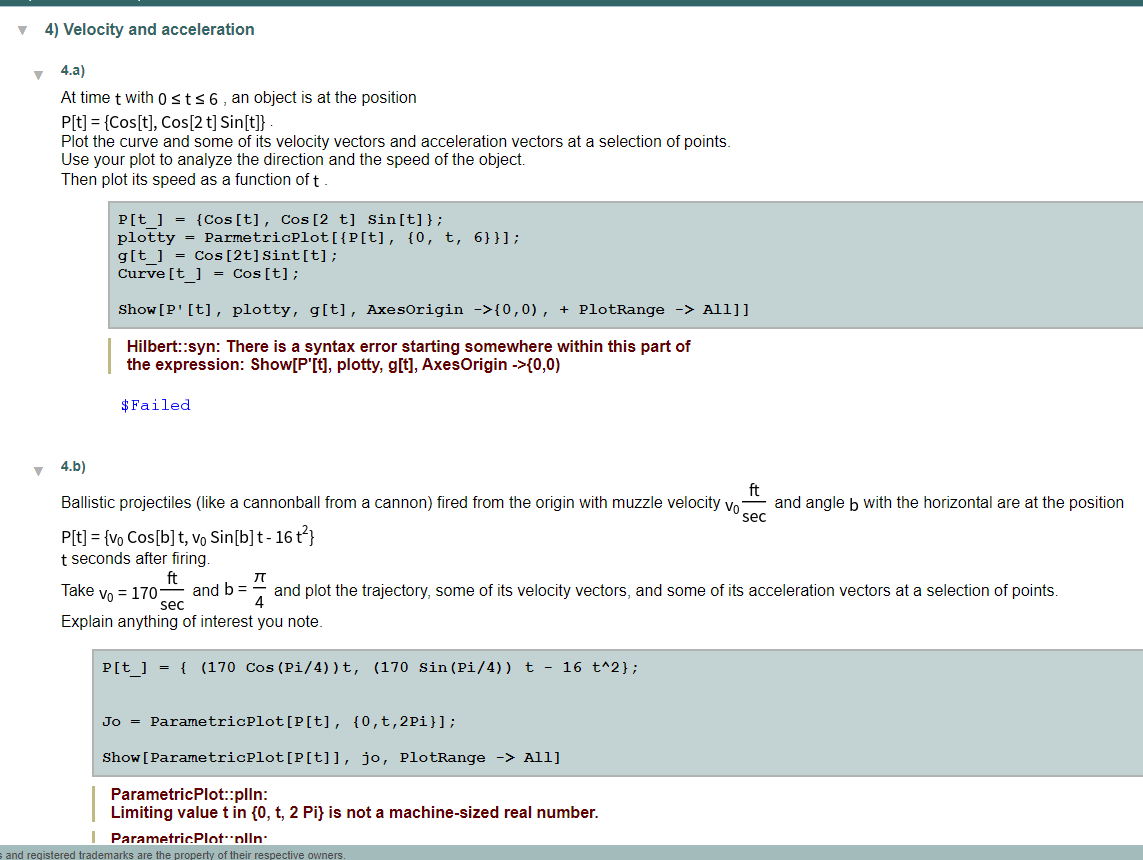
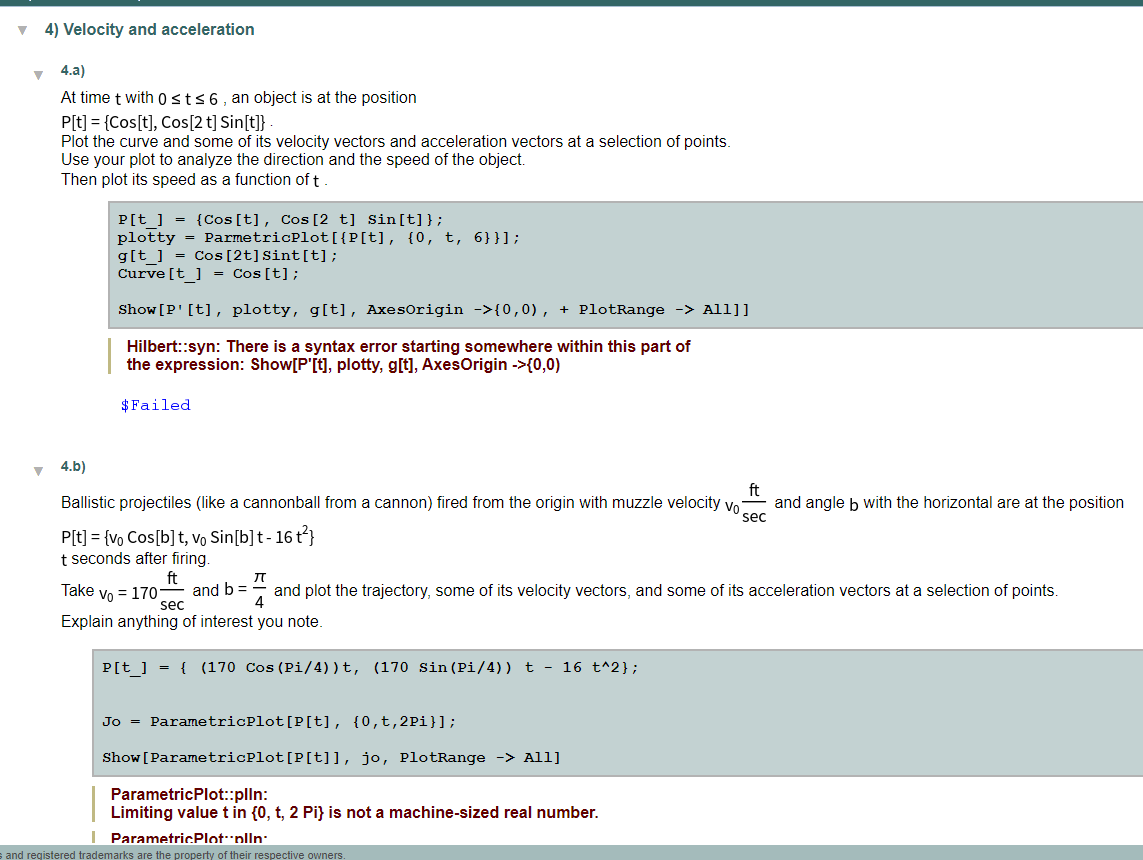
v 4} Velocity and acceleration ,. ma} At time twilh [I s t s 6 , an object is at the position P[t] = {Cos[t], Cos [2 t] Sin[t]} . Plot the curve and some of its velocity vectors and acceleration vectors at a selection of points. Use your plot to analyze the direction and the speed of the object. Then plot ils speed as a function oft . Hilbert::syn: There is a syntax error starting somewhere within this part of the expression: ShowIP' [t], plotty, g[t], AxesOrigin ->{(l,t}] $Failed '. 4th: Ballistic projectiles (like a cannonball from a cannon) red from the origin with muzzle velocity val and angle b with the horizontal are at the position 5 EC P[t] = {Va Cos[b] t, v0 Sin[b] t- 16 t2} t seconds after ling. in Take v0 = 170 and h = I and plot the trajectory, some of its velocity vectors, and some of its acceleration vectors at a selection of points. sec Explain anything of interest you note. ParametricPlot::plln: lJmiting value t in {0, t, 2 Pi} is not a machine-sized real number. I ParametrinPlnf'mlln' 4.c) For P[t] = {3 Sin[t], 5 Sin[ 12, 2 Cos[t]) , plot in true scale the motion of the object for 0 s t s 5 , including several velocity vectors. Then, on a separate plot, show the motion of the object for 0 s t s 5 , including several tangential components of acceleration. On a third plot, show the motion of the object for 0 S t s 5 , including several tangential and normal components of acceleration. Discuss what each plot reveals. P[t] = {x[t] , Y[t] , z[t]) = {3 sin [t], 5 sin [t/2]^2, 2 Cos[t] ; ParametricPlot[ , {0, t,5) Syntax::com: Warning: Comma encountered with no adjacent expression. The expression will be treated as Null. . ToExpression::sntxi: Incomplete expression; more input is needed . Hilbert::syn: There is a syntax error starting somewhere within this part of the expression: P[t] = {X[t], Y[t], Z[t]) = {3 Sin[t], 5 Sin[t/2]^2, 2 Cos[t]; ParametricPlot[ , {0,t,5} $ Failed V 4.d.i) An object is at P[t] = {8 Sin[t], 4 Cos[t]} at time t . Plot in true scale the motion of the object for 0 s t s 2 71 - including several velocity vectors. Then, on a separate plot, show in true scale the motion of the object for 0 s ts 2 7t 3 including several tangential and normal components of acceleration. Discuss what each plot reveals. Finally, show the plots together and discuss relations between them. V 4.d.ii) For Osts 2 1 3 - the object in part i) is constrained to move on an ellipse. Suppose, at the instantt= the object is released from all constraints and allowed to move of its own free will independent of any accelerations due to forces. Plot the path the object takes. Tip: Does it continue along on the ellinse or does it do something else